План-конспект урока по математике "Метод сечений многогранников"

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

1. Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.

2. В задачах используются в основном простейшие многогранники.

3. Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

- что значит построить сечение многогранника плоскостью;

- как могут располагаться относительно друг друга многогранник и плоскость;

- как задается плоскость;

- когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

- тремя точками;

- прямой и точкой;

- двумя параллельными прямыми;

- двумя пересекающимися прямыми,

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

1. Метод следов.

2. Метод вспомогательных сечений.

3. Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

- построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;

- построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;

- построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;

- построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;

- построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

Цель урока:

развитие навыков решения стереометрических задач на сечение многогранников, используя трехмерную графику.

Задачи:

совершенствовать и закрепить знания учащихся в решении задач на сечение многогранников на основе их абстрактного (пространственного) мышления.

- развить логическое мышление, образное восприятие.

- создать условия для развития положительной мотивации к изучению предмета, подготовке к сдаче экзамена, снятию трудностей при решении подобных задач.

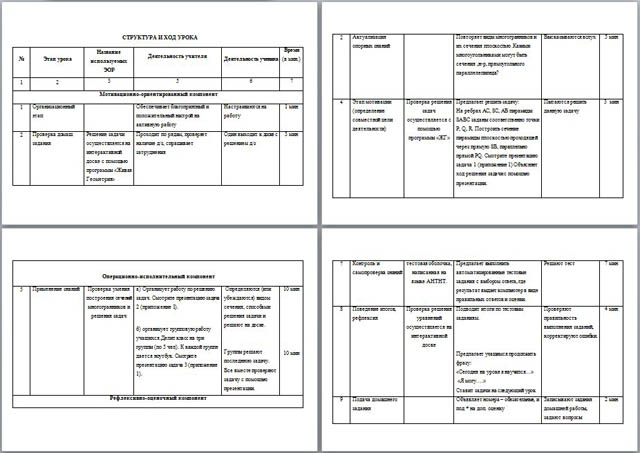
Структура и ход урока.

Мотивационно-ориентированный компонент.

1. Организационный этап.

Учитель обеспечивает благоприятный и положительный настрой на активную работу.

2. Проверка домаш. задания.

Решение задачи осуществляется на интерактивной доске с помощью программы «Живая Геометрия».

Учитель проходит по рядам, проверяет наличие д/з, спрашивает затруднения.

3. Актуализация опорных знаний.

Учитель повторяет виды многогранников и их сечения плоскостью. Какими многоугольниками могут быть сечения, н-р, прямоугольного параллелепипеда?

Весь материал - в документе.