В качестве электронного приложения к уроку используется программа «Сечения цилиндра, конуса, куба», выполненная в среде Power Point и с использованием кадровой анимации графического редактора Flash MX.
Методическое руководство к программе «Сечения цилиндра, конуса, куба».
Электронная презентация состоит из 29 слайдов и предназначена для работы учеников не только на компьютере, но и с интерактивной доской. Первый слайд презентации – титульный. Он содержит тему урока и фамилию разработчика.
На втором слайде представлена анимационная картинка, демонстрирующая пространственные тела. Третий слайд презентации является ключевым и дает возможность учащимся выбрать фигуру для построения сечения, предварительно ознакомившись с основными принципами построения сечений. Меню этого слайда позволяет также выбрать разделы «Математический диктант» и «Решение задач» для самоконтроля после ознакомительного этапа.
На слайде изображены цилиндр, конус и куб. Нажатие на каждую из этих фигур позволяет по гиперссылке перейти на слайды с анимационными картинками, демонстрирующими всевозможные виды сечений этих тел и технику их построения.
Здесь же появляется возможность у учащихся выполнить построение этих сечений на интерактивной доске. Раздел «Математический диктант» позволяет проверить себя по простейшим вопросам теории. Раздел «Решение задач» позволяет сначала выполнить построение некоторых сечений куба с использованием электронного маркера и интерактивной доски, а также решить задачи, выполненные в виде теста. В случае неверного решения задачи на экране будет появляться сообщение об ошибке. Если задача решается верно, то появляется возможность перейти к решению следующей задачи.
Работа с электронной презентацией осуществляется с помощью интерактивной доски, что дает возможность не пользоваться традиционной доской и мелом. Время на уроке используется более рационально (не надо тратить время на построение чертежа; из-за наличия картинок в электронном виде, иллюстрирующих рассматриваемые задачи, темп работы с учащимися ускоряется). За счет наглядности, ярких образов и популярности компьютерных технологий у старшеклассников активизируется интерес к изучаемому предмету и появляется стимул к освоению более сложных тем.
Интегрирующие и дидактические цели:
Знакомство учеников с основными принципами построения простейших сечений куба, цилиндра, конуса.
Формирование навыков решения простейших задач на построение сечений.
Развитие пространственного зрения.
Развитие навыков самоконтроля и самооценки.
Овладение технологией работы у интерактивной доски.
Средства:
Компьютер с проектором, интерактивная доска.
Основные этапы урока.
Демонстрационно-ознакомительный.
Тренировочный.
Контролирующий.
Подведение итогов.

1 этап.
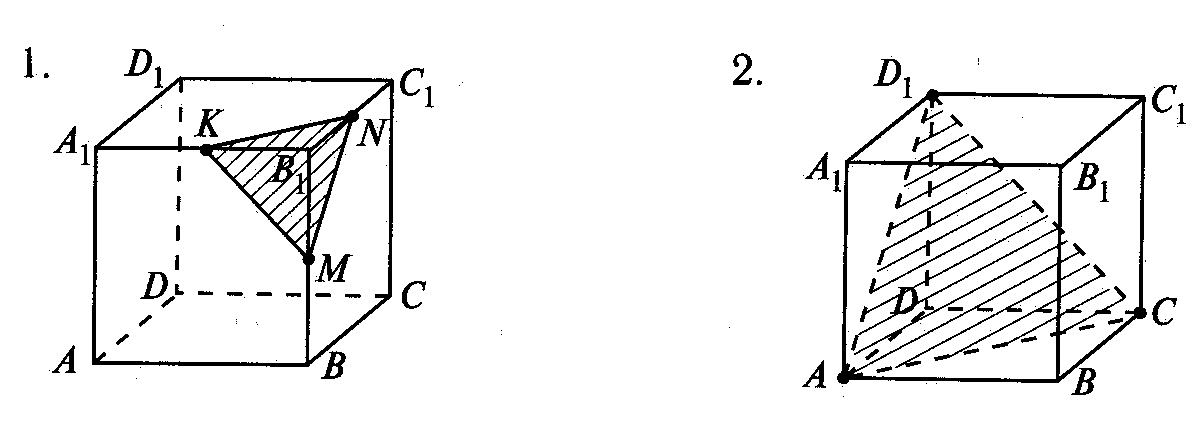
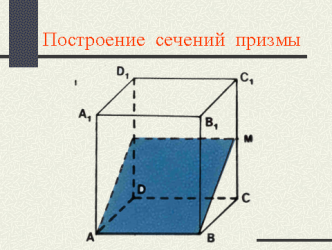
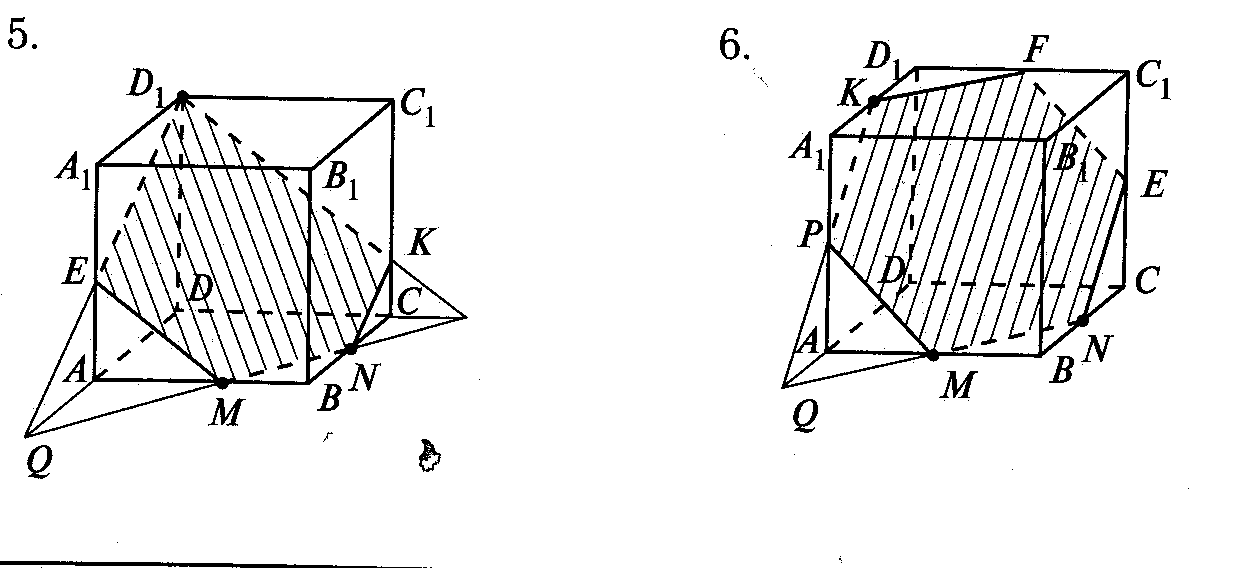
Начинается показ электронной презентации на интерактивной доске. Из основного меню простым нажатием на изображение цилиндра, конуса и куба, осуществляется переход на слайды, связанные с построением сечений этих пространственных фигур. Ученики сначала знакомятся с основными видами сечений цилиндра и конуса, имея возможность выполнить построения на интерактивной доске и в тетради с печатной основой. Затем на интерактивной доске демонстрируются сечения куба секущими плоскостями, проходящими через три заданные точки, расположенные определенным образом на ребрах так, что в сечении появляются треугольники, четырехугольники, пятиугольники и шестиугольники.
2 этап.
В рабочих тетрадях учащиеся имеют возможность выполнить задачи на построение сечений, ответить на вопросы. Кроме того, есть возможность потренироваться выполнять задачи на построение сечений на интерактивной доске.
3 этап.
На данном этапе весь класс разбивается на две группы: с хорошей математической подготовкой и с недостаточной математической подготовкой.
На интерактивной доске демонстрируются задания из раздела «Математический диктант». «Слабые» учащиеся отвечают на вопросы в тетрадях с печатной основой. Им предоставляется возможность проверить свое решение, поскольку на интерактивной доске «сильные» ученики выписывают основные формулы или положения. Входя в раздел «Решение задач», ученики имеют возможность сначала выполнить построение сечений куба, проходящих через три заданные точки, а затем четыре задания в виде теста. В случае верного решения идет переход на слайд с очередной задачей. В случае ошибки будет дано сообщение о ней и предложено решить задачу заново. Все эти этапы будут отражаться на интерактивной доске учащимися. Старшеклассники с недостаточной математической подготовкой могут строить простейшие сечения, «сильные» ученики – более сложные и решать задачи.
4 этап
Каждый ученик:
Записывает количество и номера выполненных заданий.
Записывает номера задач, которые вызвали затруднения.
Подводятся итоги. Выставляются оценки. Учитель дает домашнее задание классу с объяснением его выполнения.
Домашнее задание: № 84, 529, 549(б), 551(в).
Приложения к уроку
Математический диктант.
Верны ли следующие утверждения?
1. Сечениями куба могут быть шестиугольники, семиугольники.
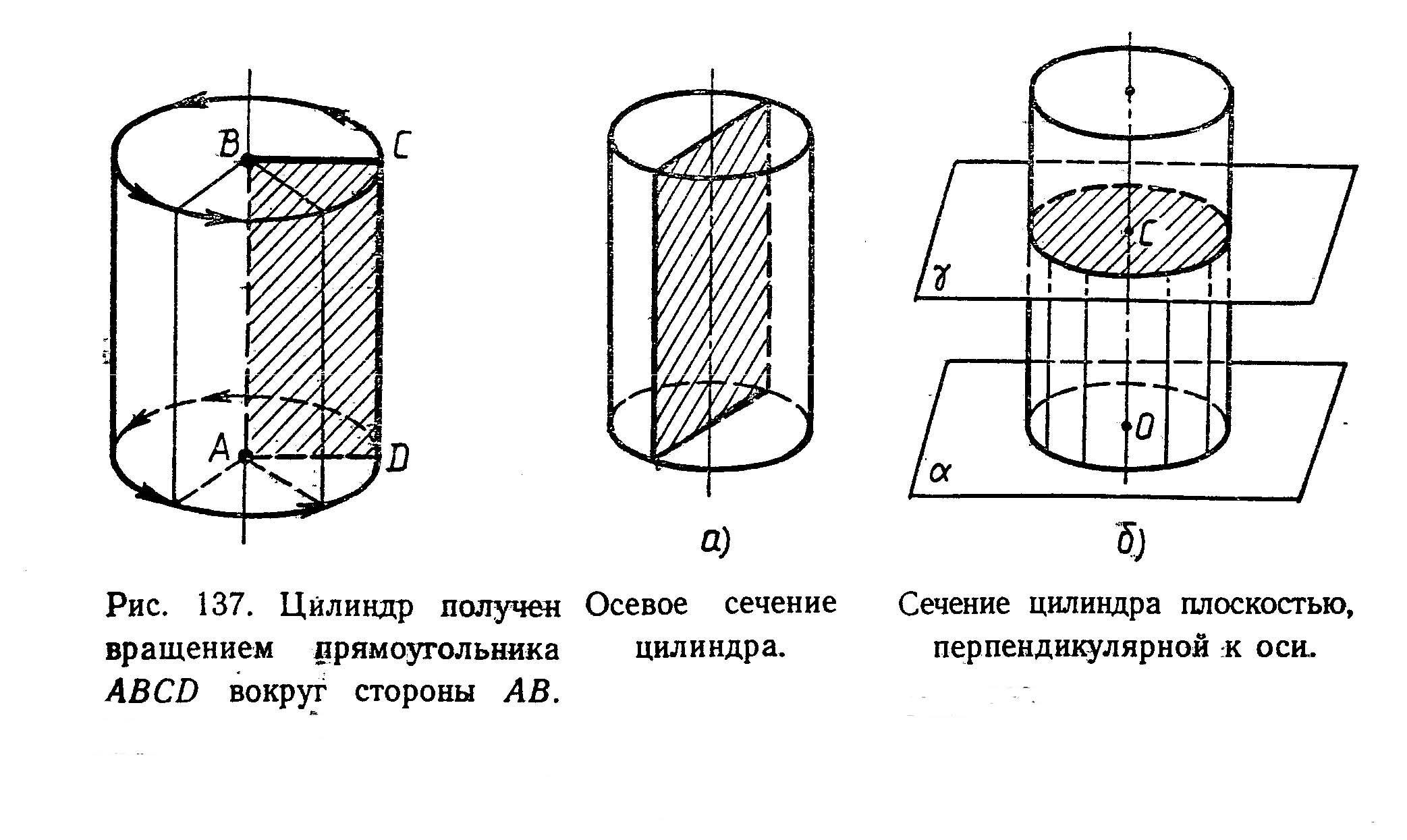
2. Осевым сечением цилиндра является квадрат со стороной 2 см. Площадь боковой поверхности цилиндра равна 4π см2.
3. В цилиндре радиуса 3см проведено сечение, параллельное основанию цилиндра. Его площадь равна 9π см2.
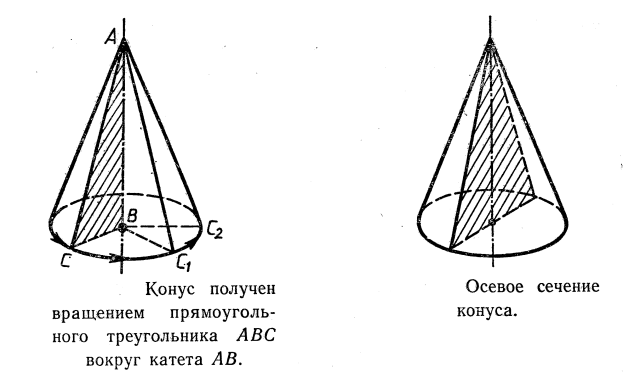
4. Осевым сечением конуса является равносторонний треугольник с площадью 9*31/2 см2. Длина образующей конуса равна 6 см.
5. В конусе радиуса 4 см и высотой 8 см проведено сечение перпендикулярно оси конуса радиуса 2 см. Тогда расстояние от вершины конуса да этого сечения равно 4 см.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



 4. Осевым сечением конуса является равносторонний треугольник с площадью 9
4. Осевым сечением конуса является равносторонний треугольник с площадью 9 см2 . Длина образующей конуса равна 6 см.
см2 . Длина образующей конуса равна 6 см.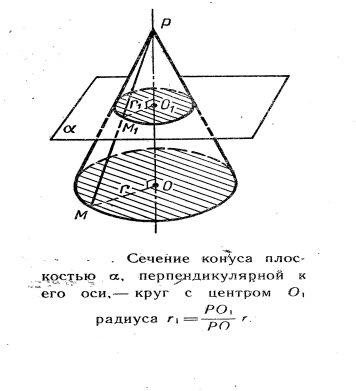 5. В конусе радиуса 4 см и высотой 8 см проведено сечение перпендикулярно оси конуса радиуса 2 см. Тогда расстояние от вершины конуса да этого сечения равно 4 см.
5. В конусе радиуса 4 см и высотой 8 см проведено сечение перпендикулярно оси конуса радиуса 2 см. Тогда расстояние от вершины конуса да этого сечения равно 4 см.








 Методическое руководство к уроку математики с использованием интерактивной доски по теме «Некоторые сечения цилиндра, конуса, куба» (0.46 MB)
Методическое руководство к уроку математики с использованием интерактивной доски по теме «Некоторые сечения цилиндра, конуса, куба» (0.46 MB)
 0
0 860
860 32
32 Нравится
0
Нравится
0









