Урок математики "Ромб и квадрат, их свойства"

Цели:

1. Ввести понятия ромба и квадрата как частных видов параллелограмма;

2. Рассмотреть свойства ромба и квадрата и показать их применение в процессе решения задач;

3. Совершенствовать навыки решения задач.

4. Воспитывать аккуратность, культуру и организацию труда.

5. Развивать интеллектуальные умения: сравнение, анализ, синтез и способность к самооценке и самоанализу.

Оборудование: наглядный материал, раздаточный материал с устными заданиями, теоретической самостоятельной работой, магические квадраты, карточки для работы в группах.

Тип урока: комбинированный.

План урока:

Организационный этап. (1 мин)

Актуализация опорных знаний. (10 мин)

Работа по обработке навыков и умений. (25 мин)

Домашнее задание. (2 мин)

Мозговая атака (5 мин)

Подведение итогов урока. (2 мин)

Ход урока:

1. Организационный этап.

Подготовить учащихся к работе на уроке. Взаимное приветствие; проверка подготовленности учащихся к уроку (рабочее место, внешний вид); организация внимания.

2. Актуализация опорных знаний

Выборочная проверка домашнего задания.

Определение, свойство и признак прямоугольника - 2 ученика у доски.

Остальные решение задачи на карточках:

Карточка №1.

Найдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см.

Карточка №2.

В прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60^◦. Найдите диагональ АС.

Решение – смотрите документ.

3. Работа по обработке навыков и умений

 - Является ли параллелограммом четырёхугольник АВСD? Почему?

 - Такой четырёхугольник является ещё одним частным случаем параллелограмма и называется ромбом.

Определение. Ромбом называется параллелограмм, у которого все стороны равны.

 - Перечислите все свойства ромба как частного вида параллелограмма.

В ромбе все стороны равны. (по определению ромба)

В ромбе противоположные углы равны.

В ромбе противоположные стороны попарно параллельны.

В ромбе диагонали точкой пересечения делятся пополам.

 - Выясните, каким ещё особым свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам.

(Работа в парах с последующим обсуждением свойства диагоналей ромба).

 Инструктаж к работе в парах по изучению свойства ромба.

Учитель инструктирует учащихся: о способе деятельности, о месте нахождения материала.

Весь материал – смотрите документ.

Учитель математики:

Аметова Э.М..

21.10.2011г.

Цели:

1.Ввести понятия ромба и квадрата как частных видов параллелограмма;

2.Рассмотреть свойства ромба и квадрата и показать их применение в процессе решения задач;

3.Совершенствовать навыки решения задач.

4.Воспитывать аккуратность, культуру и организацию труда.

5.Развивать интеллектуальные умения: сравнение, анализ, синтез и способность к самооценке и самоанализу.

Оборудование: наглядный материал, раздаточный материал с устными заданиями, теоретической самостоятельной работой, магические квадраты, карточки для работы в группах.

Тип урока: комбинированный.

План урока:

1. Организационный этап. (1 мин)

2. Актуализация опорных знаний. (10 мин)

3. Работа по обработке навыков и умений. (25 мин)

4. Домашнее задание.(2 мин)

5. Мозговая атака (5 мин)

6. Подведение итогов урока.(2 мин)

Ход урока:

2. Актуализация опорных знаний

• Выборочная проверка домашнего задания.

• Определение, свойство и признак прямоугольника - 2 ученика у доски.

• Остальные решение задачи на карточках:

Карточка №1.

Н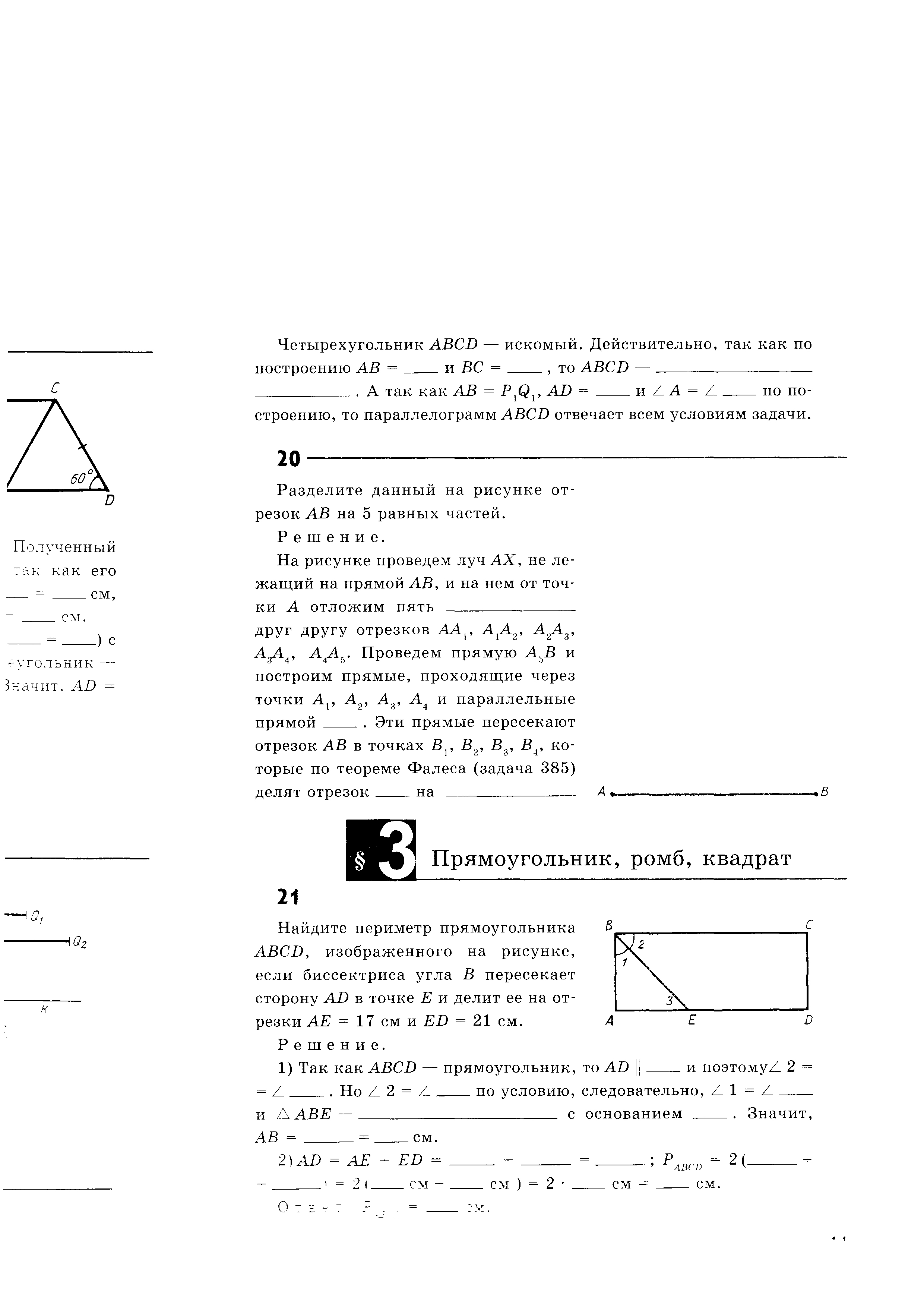айдите периметр прямоугольника ABCD, изображённого на рисунке, если биссектриса угла В пересекает сторону AD в точке Е и делит её на отрезки АЕ = 17 см и ЕD = 21 см.

Решение.

1. Так как ABCD – прямоугольник, то AD | | ____ и поэтому ___.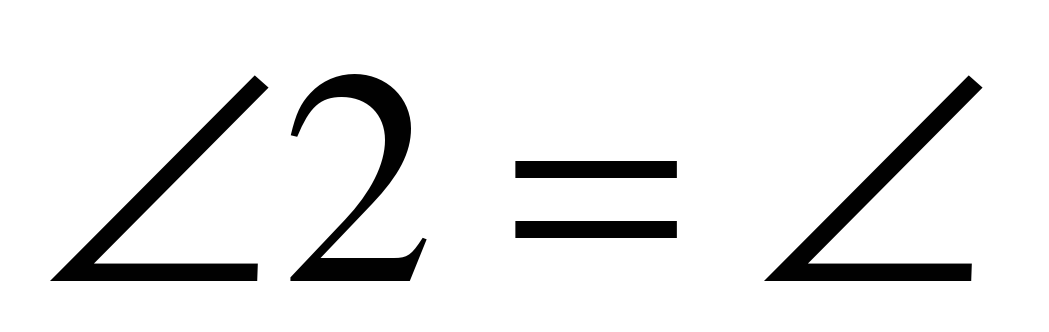

Но 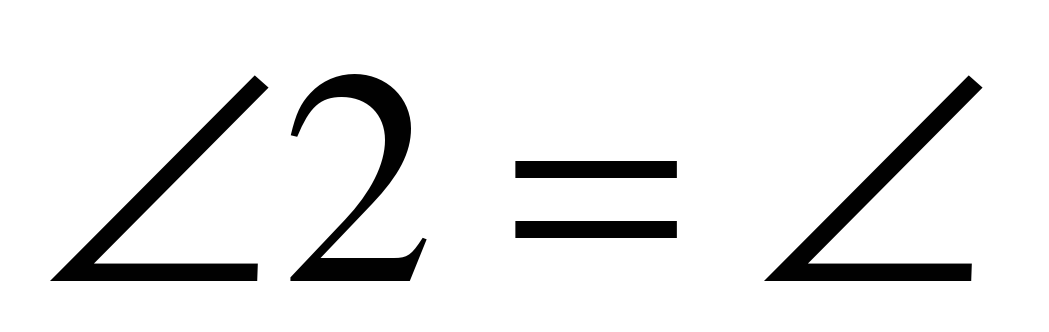___ по условию, следовательно, 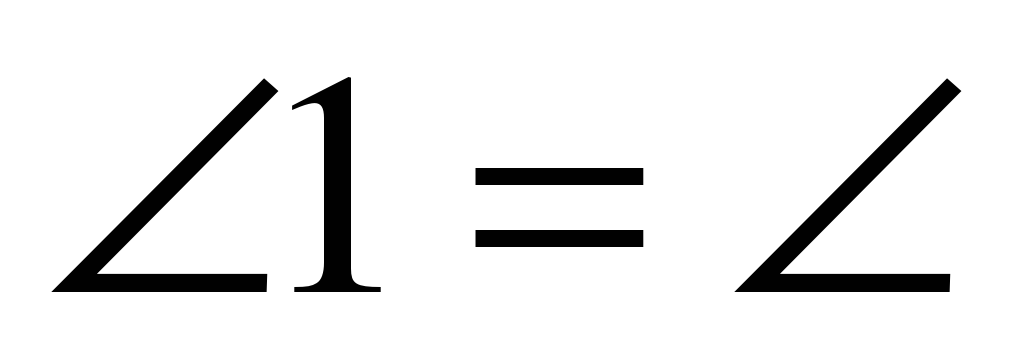__ и ▲ABE - ____________

с основанием ___. Значит, АВ = ___ = ___ см.

2) AD = AE + ED = ___ + ___ = ___; P_ABCD = 2*(____ + ____) =

=2*(___ см + ___см) = 2*___ см = ___см.

Ответ: P_ABCD =___см.

Карточка №2.

В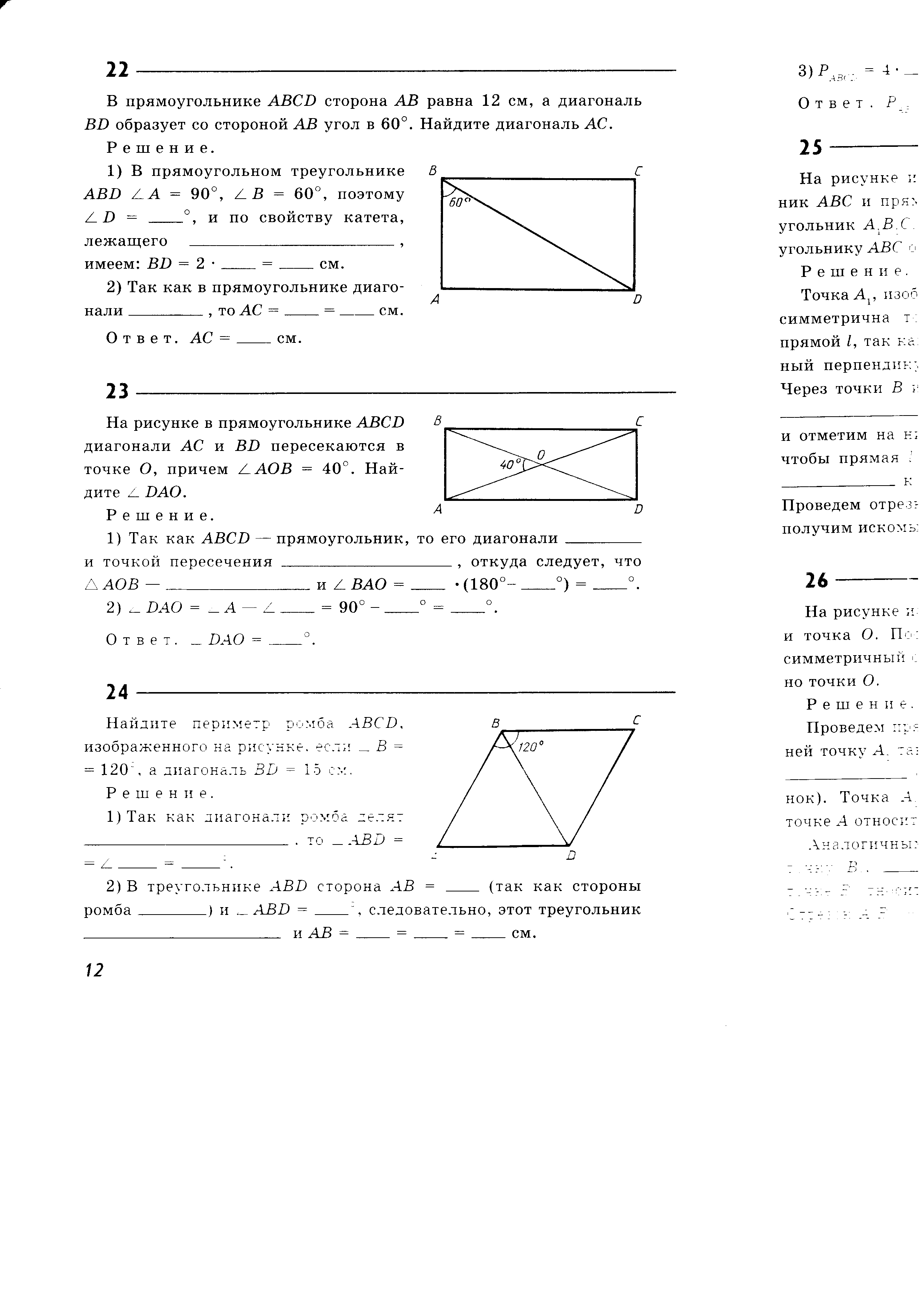 прямоугольнике ABCD сторона АВ = 12 см, а диагональ BD образует со стороной АВ угол в 60^◦. Найдите диагональ АС.

Решение.

1. В прямоугольном треугольнике ABD 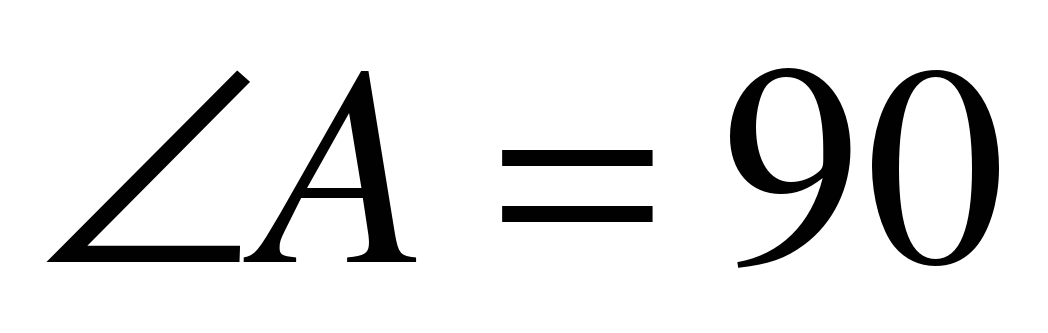^◦, ^◦, поэтому ___^◦, и по свойству катета, лежащего _______________, имеем: BD = 2*__=__см.

2. Так как в прямоугольнике диагонали ______, то АС = ___=___см.

Ответ: АС= ___ см.

Карточка №3.

В прямоугольнике ABCD диагонали АС и BD пересекаются в точке О, причём

^◦. Найдите .

Решение.

1) Так как ABCD – прямоугольник, то его диагонали ______ и точкой пересечения _____________________, откуда следует, что ▲АОВ - _________ и = ___*(180^◦ - ___^◦) = ___^◦.

2) = - ___ = 90^◦ - ___ ^◦ = ___^◦.

Ответ: =___^◦.

3.Работа по обработке навыков и умений

- Является ли параллелограммом четырёхугольник АВСD? Почему?

-Такой четырёхугольник является ещё одним частным случаем параллелограмма и называется ромбом.

Определение. Ромбом называется параллелограмм, у которого все стороны равны.

- Перечислите все свойства ромба как частного вида параллелограмма.

• В ромбе все стороны равны. (по определению ромба)

• В ромбе противоположные углы равны.

• В ромбе противоположные стороны попарно параллельны.

• В ромбе диагонали точкой пересечения делятся пополам.

- Выясните, каким ещё особым свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам.

(Работа в парах с последующим обсуждением свойства диагоналей ромба).

Инструктаж к работе в парах по изучению свойства ромба.

Учитель инструктирует учащихся: о способе деятельности, о месте нахождения материала.

Задача пар:

1. прочитать доказательство;

2. определить основную идею доказательства;

3. выделить этапы и шаги доказательства;

4) дать обоснование каждому шагу

1. подготовить выступление от пары в защиту приведенного доказательства.

Самостоятельная работа в парах по изучению доказательства свойства ромба.

Публичная защита доказательства.

Одна из пар начинает свое выступление с формулировки свойства ромба.

(Идет активное обсуждение доказательства, в ходе которого с помощью вопросов учителя и учащихся обосновывается тот или иной вариант.)

Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Доказать: АСBD

(, , )

Доказательство:

AB = AD (по определению ромба), ▲BAD равнобедренный.

АО = ОС, ВО = DО (т.к. ромб – параллелограмм), АО – медиана равнобедренного ▲BAD, АО – высота и биссектриса ▲BAD.

Поэтому АСBD и .

(Равенство остальных углов ромба доказываются аналогично).

-Является ли прямоугольником четырёхугольник АВСD? В С

- Почему?

А D

- Такой четырёхугольник является ещё частным случаем прямоугольника, а значит и параллелограмма, и ромба - называется квадратом.

Определение. Квадратом называется прямоугольник, у которого все стороны равны.

- Значит квадрат обладает всеми свойствами прямоугольника и ромба.

- Перечислите все свойства квадрата.

• Все углы квадрата прямые.

• Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Физкультминутка. ( «Истинно-ложно»)

Я скажу несколько математических предложений. Если предложение верное, то вы сидите, если оно ложное, то вы встаёте, и кто-то из вас объясняет, почему ложное.

• Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. (+)

• В параллелограмме противоположные стороны и противоположные углы равны. (+)

• В параллелограмме диагонали равны. (-)

• В параллелограмме диагонали точкой пересечения делятся пополам. (+)

• Диагонали прямоугольника точкой пересечения делятся пополам. (+)

• Сумма углов выпуклого четырёхугольника равна 180^◦. (-)

• В прямоугольнике противоположные стороны равны. (+)

• Ромб обладает всеми свойствами прямоугольника. (-)

• Квадрат не обладает всеми свойствами ромба. (-)

• Квадрат обладает всеми свойствами параллелограмма, прямоугольника, ромба. (+)

4. Домашнее задание.

Пункт 15, стр. 88-90 - повторить

Задание 14, Iгр.– №2; IIгр.–№ 4.

5.Мозговая атака.

Задача. Найдите периметр ромба ABCD, изображённого на рисунке, если ^◦, а диагональ BD = 15 см.

Решение.

1)Так как диагонали ромба делят углы пополам,

то ABD = DBC = 60^◦.

2)В треугольнике ABD сторона АВ = AD (так как стороны ромба равны)

следовательно, этот треугольник равнобедренный с основанием ВD и

ABD =ADВ = 60^◦. Так как сумма углов треугольника равна 180^◦, то DАВ= 60^◦, следовательно, треугольник ABD равносторонний, значит

АВ = BD = AD = 15 см

3)P_ABCD =4 * 15 см = 60 см. Ответ: P_ABCD = 60 см.

Теоретическая самостоятельная работа. (Самоанализ и самооценка)

- Заполните таблицу, отметив знаки + (да) и – (нет).

- Проверьте самостоятельно и поставьте себе оценку.

Критерий выставления оценки:

Оценка «5» - все ответы верные.

Оценка «4» - допущены ошибки.

Оценка «3» - допущены ошибки.

Оценка «2» - допущены ошибки.

Учащиеся подсчитывают «+», заработанные на уроке, и пользуясь алгоритмом, предложенным учителем, выставляют себе отметку за урок.

6.Итог урока.

- Что нового вы узнали сегодня на уроке?

- Дайте определение ромба? Квадрата?

- Назовите особое свойство ромба?

- Перечислите свойства квадрата?

Учащиеся рассказывают о том, чем они занимались на уроке, какие умения у них развиты

хорошо, какие задания вызвали затруднения.

Мне было приятно сегодня с вами работать!

8