Цель:
обобщить знания учащихся по теме «Четырехугольники», закрепить навыки решения основных типов заданий, развивать умение подводить под определение и выводить следствия из определения, способствовать формированию умения применять приёмы сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию; развитие математического кругозора, мышления, речи, внимания и памяти, содействовать воспитанию интереса к математике, активности.
Ход урока.
- Д. Пойа однажды сказал: «Владение математикой - умение решать задачи». Но чтобы научиться решать задачи, нужно знать теоретический материал. Кроме этого, нельзя научиться решать задачи, пока не будешь решать задачи, как нельзя научиться прыгать, не пробую прыгать. Давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем учиться решать задачи с большим желанием. Ведь эти знания и умения пригодятся вам в дальнейшем.
Сегодня у нас заключительный урок по теме: «Четырехугольники». Повторяем, обобщаем изученный материал, методы и приёмы решения задач на определение вида четырехугольника и вычисления его элементов.
- Проверка домашнего задания.
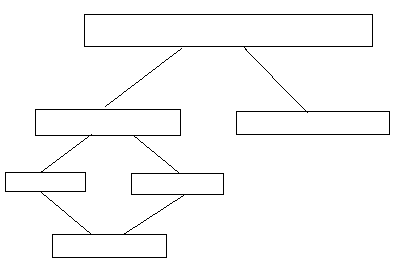
- Защита схемы. Расположите понятия: «Прямоугольник», «Ромб», «Квадрат», «Параллелограмм», «Трапеция», «Четырехугольник» - в схеме в порядке соподчинения, от более общего понятия к менее общему.
Ответьте на вопросы:
Почему понятия расположены именно так (доказать, используя определение каждого понятия)?
Дать 3 определения квадрата, используя понятия ромба, прямоугольника и параллелограмма.
- Докажите свойство диагоналей параллелограмма.
- Сформулируйте признаки параллелограмма, прямоугольника, ромба, квадрата.
- Математический диктант.
Закончите предложения:
- Противоположные стороны равны у . . .
- Диагонали равны у. . .
- Диагонали точкой пересечения делятся пополам у. . .
- Все углы равны у. . .
- Противоположные углы равны у. . .
- Углы, прилежащие к основанию, равны у. . .
- Диагонали перпендикулярны у. . .
- Диагонали делят углы пополам у. . .
- Все стороны равны у. . .
- Диагонали равны и перпендикулярны у. . .
- Решение задач.
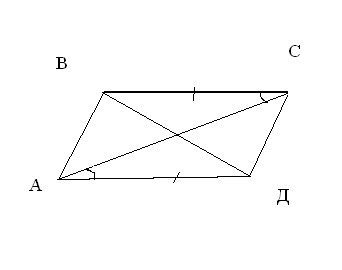
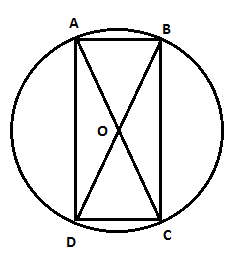
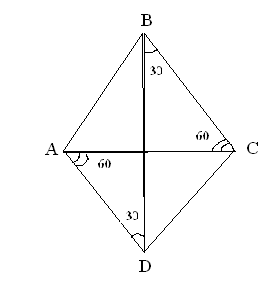
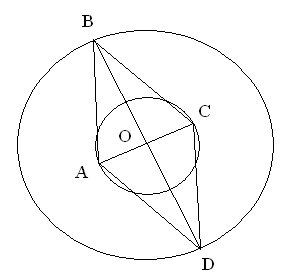
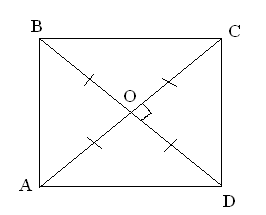
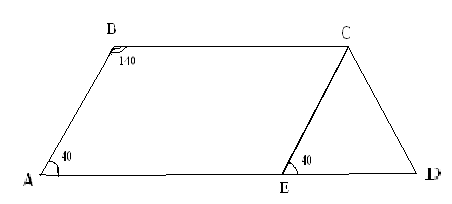
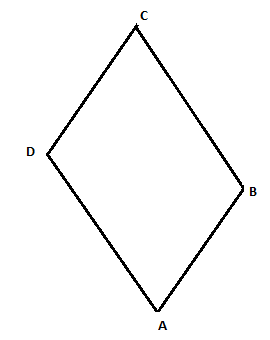
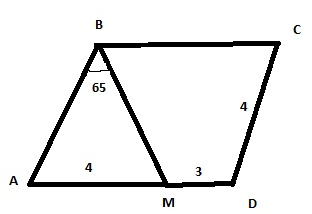
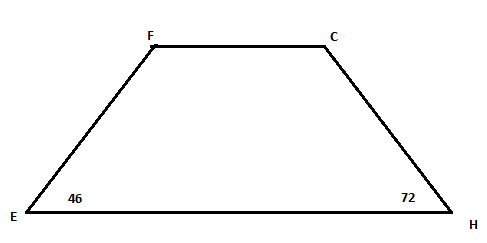
В задачах 1 - 6 определите вид четырехугольника.
смотрите документ
IV. Итог урока.
Итак, как можно доказать, что четырехугольник является параллелограммом?
Как доказать, что параллелограмм является ромбом, прямоугольником, квадратом?
Какими свойствами обладают параллелограмм, прямоугольник, ромб, квадрат?
V. Домашнее задание: придумать и решить 2 задачи по теме «Четырехугольники».

 Получите свидетельство
Получите свидетельство Вход
Вход


 1.
1. 
 8
8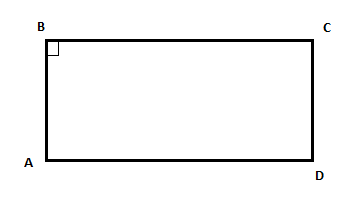

 11
11








 Четырёхугольники (0.11 MB)
Четырёхугольники (0.11 MB)
 0
0 695
695 42
42 Нравится
0
Нравится
0


