Практическая работа
Измерить длину окружности С с помощью нитки. Записать в тетрадь: С=
Измерить диаметр d этой окружности. Записать: d=
Найти отношение длины окружности C к d, результат округлить до единиц. Записать: С:d=
Задачи
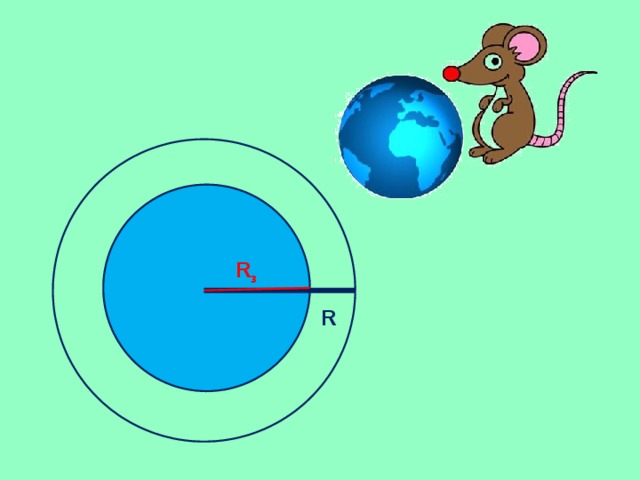
Предполагая, что Земля – идеальный шар радиуса 6400 км, натянем вдоль экватора проволоку. Затем по каким-то причинам проволока удлинилась ровно на один метр и равномерно отошла от земли. Сможет ли под этой проволокой пролезть мышь? Определить размер щели.
Диаметр колеса велосипеда равен 70 см. за 2 мин колесо сделало 200 оборотов. С какой скоростью едет велосипед?
Практическая работа
Измерить длину окружности С с помощью нитки. Записать в тетрадь: С=
Измерить диаметр d этой окружности. Записать: d=
Найти отношение длины окружности C к d, результат округлить до единиц. Записать: С:d=
Задачи
Предполагая, что Земля – идеальный шар радиуса 6400 км, натянем вдоль экватора проволоку. Затем по каким-то причинам проволока удлинилась ровно на один метр и равномерно отошла от земли. Сможет ли под этой проволокой пролезть мышь? Определить размер щели.
Диаметр колеса велосипеда равен 70 см. за 2 мин колесо сделало 200 оборотов. С какой скоростью едет велосипед?
Практическая работа
Точку А картонного круга совместить с отметкой 0 линейки. Прокатить картонный круг вдоль линейки от точки А до точки А.
Измерить длину полученного отрезка. Записать в тетрадь: С=
Измерить диаметр d окружности. Записать: d=
Найти отношение длины окружности C к d, результат округлить до единиц. Записать: С:d=
Задачи
Предполагая, что Земля – идеальный шар радиуса 6400 км, натянем вдоль экватора проволоку. Затем по каким-то причинам проволока удлинилась ровно на один метр и равномерно отошла от земли. Сможет ли под этой проволокой пролезть мышь? Определить размер щели.
Диаметр колеса велосипеда равен 70 см. за 2 мин колесо сделало 200 оборотов. С какой скоростью едет велосипед?
Практическая работа
Точку А картонного круга совместить с отметкой 0 линейки. Прокатить картонный круг вдоль линейки от точки А до точки А.
Измерить длину полученного отрезка. Записать в тетрадь: С=
Измерить диаметр d окружности. Записать: d=
Найти отношение длины окружности C к d, результат округлить до единиц. Записать: С:d=
Задачи
Предполагая, что Земля – идеальный шар радиуса 6400 км, натянем вдоль экватора проволоку. Затем по каким-то причинам проволока удлинилась ровно на один метр и равномерно отошла от земли. Сможет ли под этой проволокой пролезть мышь? Определить размер щели.
Диаметр колеса велосипеда равен 70 см. за 2 мин колесо сделало 200 оборотов. С какой скоростью едет велосипед?

 Получите свидетельство
Получите свидетельство Вход
Вход
























 Урок "Длина окружности" (640.83 KB)
Урок "Длина окружности" (640.83 KB)
 0
0 1268
1268 22
22 Нравится
0
Нравится
0









