Цель:
- обеспечить в ходе урока знакомство с числом П; усвоение формул длины окружности и площади круга;
- развить представление учащихся о числах, развивать самостоятельность в работе;
-прививать интерес к историческим сведениям математики; учить трудолюбию, аккуратности.
Оборудование:
Раздаточный материал: цилиндр, линейка, нитки; таблицы: «число П», « Это я знаю и помню прекрасно».
Ход урока:
I Орг. Момент. Сообщение темы, цели урока.
- Тема сегодняшнего урока « Длина окружности и площадь круга»
- Как вы думаете, как можно измерить длину окружности?
+ нитки, формулы
-Сегодня на уроке мы выведем формулу длины окружности и площади круга, познакомимся с древнейшим числом, будем учиться видеть красоту чертежей, покажите аккуратность и точность пользования измерительными приборами.
II Актуализация знаний и умений учащихся.
- Поработаем устно ( запись на доске)
1) что означает : а, в в
2) вычислите: 4; 7; 0; (0,4); (0,9); (1/2); (1/5)
3) округлите: 3,14159265 до целых, десятых, тысячных, десятитысячных
4) посмотрите на чертёж и ответьте на вопросы:
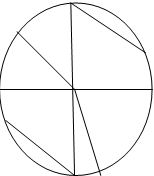
-назовите центр окружности (+ О)
- чем является отрезок АВ (+диаметр)
-есть ли ещё на чертеже диаметры (+ ЕС)
- чем является отрезок ОВ (+ радиус)
- есть ли ещё на чертеже радиусы (+ ОЕ, ОД, ОА, ОС, ОК)
- как называется отрезок МС (+хорда)
- есть ли ещё на чертеже хорды (+ ЕР)
-что можно сказать про диаметр окружности (+ проходит через центр окружности и состоит из двух радиусов)
-можно ли измерить хорду, радиус, диаметр (+ да)
-какую геометрическую фигуру ограничивает окружность ( круг)
-у окружности мы с вами можем измерить длину, а у круга площадь.
III Исследовательская работа
( раздаточный материал: цилиндр; нитки, красный радиус 1.8, зелёный радиус 1.4)
- Сегодня мы научимся вычислять длину окружности и площадь круга. Для этого мы выведем формулы для вычисления длины окружности и площади круга.
- Откроем тетради. Запишем число, классная работа, тему урока.
- У вас на столах цилиндры. Возьмите каждый свой цилиндр в руки и посмотрите внимательно, что на нём отмечено (+ центр, диаметр)
- а что у вас лежит ещё на столе (+ линейка, нитки)
-Как вы думаете, для чего вам нитки (+ чтобы измерять длину окружности)
-Правильно, ниточка для того, чтобы измерить длину окружности, которая является границей круга.
-Давайте измерим длину окружности с помощью этой нитки (показ учителя как измерять)
- Теперь распрямим нить и измерим её длину, приложив её к линейке.
- Запишите её значение в тетради: С=…
- С помощью линейки измерим диаметр круга и то же запишем его значение в тетрадь: d=…
- Найдите с помощью калькуляторов отношение длины окружности к её диаметру и запишите его значение в тетрадь: С/d=…
- Какие отношения у вас получились (+ красный 3.47, зелёный 3.39)
- Молодцы, мы убедились, что вы получили отношение 3 С/d 4. Запишите его в тетрадь.
- Если бы мы ещё более точно измерили длину окружности, диаметр и ещё более точно выполнили вычисления отношения длины окружности к диаметру, то получили бы число, которое в математике обозначили буквой П.
П=3,141592653589793238462643…
IV Исторические сведения.
- Послушаем небольшое сообщение о числе Пи.
+ Число ПИ бесконечная десятичная дробь. ПИ первая буква греческого слова окружности. Впервые такое обозначение ввёл в 1706 году английский математик Джонс. Общепринятым это обозначение стало в 1736 году, после одной из работ Эйлера, великого математика, физика, астронома. Вычисление кА можно большего числа точных цифр числа П с помощью ЭВМ занимает математиков и в настоящее время. Так в 1988 году японский учёный Ясума Конеда вычислил 400 миллионов точных цифр после запятой. Это не только спортивный интерес, но это необходимо и для изучения случайных процессов.
- В школьном же курсе математике: П=3,14 , а иногда принимают П=3
- Первые 6 цифр этого числа можно запомнить по числу букв в каждом слове следующей фразы:
ЭТО Я ЗНАЮ И ПОМНЮ ПРЕКРАСНО
П= 3, 1 4 1 5 9
- Зная, что С/d=П, выразите длину окружности
+ С=Пd
- Мы говорили, что диаметр состоит из двух радиусов, значит С=2Пr
-Запишем в тетрадь: С/d=П, С=Пd, С=2Пr. Длина окружности равна произведению диаметра на число П.
V Площадь круга.
- Теперь перейдём к следующей нашей задаче: как можно измерить площадь круга (+ по формуле)
- Для нахождения площади круга мы будем пользоваться формулой S=Пr , где r-радиус круга, он обозначается так же как и окружности. А доказательство и вывод этой формулы мы будем проводить в старших классах.
VI Практическая работа
- вычислите площадь круга ( раздаточный материал: у цилиндра)
Красный: 3,14*3,24=10,1736(см)
Зелёный: 3,14* 1,96=6,1544(см)
VII Решение задач
№831 (1-сильный учащийся, 2- по образцу вместе с нами, 3- самостоятельно у доски)
- С=2Пr
С=2*3,14*24=150,72(см)
- С=2Пr
С= 2*3,14*4,7=29,516(дм)
- С=2Пr
С= 2*3,14*18,5=116,18(м)
VIII ТЕСТ – смотри документ
IX Задание на дом: п.24, №851, №852
X Итог урока. Оценки.
- С чем мы сегодня познакомились на уроке (+ с формулами длины окружности и площади круга)
- По какой формуле найдём длину окружности (+С=Пd, С=2Пr)
- Чему равняется число П (+ 3,14)
- По какой формуле вычисляется площадь круга (+S=Пr).

 Получите свидетельство
Получите свидетельство Вход
Вход
















 Длина окружности и площадь круга (18.56 КB)
Длина окружности и площадь круга (18.56 КB)
 0
0 1475
1475 121
121 Нравится
0
Нравится
0









