Конспект урока по математике по теме: "Длина окружности"

Цель урока: формирование практико - ориентированной компетенции при выведении формулы длины окружности и её применения при решении задач.

Задачи урока:

Образовательные:

обеспечение усвоения учащимися формул по нахождению длины окружности;

отработка навыков по применению данных формул при решении задач;

усвоение учащимися понятий: длина окружности, число π.

приобретение навыков исследовательской работы;

Развивающие:

развитие у учащихся коммуникативных компетентностей (культуры общения, умения работать в группах);

развитие практической направленности изучаемого материала;

развитие математической речи, памяти, умения анализировать, обобщать и делать выводы;

развитие познавательного интереса к предмету, логического мышления;

развитие творческой и мыслительной деятельности учащихся, их интеллектуальных качеств;

Воспитательные:

воспитание прилежания, аккуратности, трудолюбия, чувства коллективизма, умения слушать и слышать;

воспитание уважения и интереса к математике, умения видеть математические задачи в окружающем нас мире;

Формируемые универсальные учебные действия (УУД):

Личностные УУД: способность к самооценке на основе критерия успешности учебной деятельности.

Регулятивные УУД: умение определять и формулировать цель на уроке с помощью учителя; работать по коллективно составленному плану; оценивать правильность выполнения действий; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.

Коммуникативные УДД: умение оформлять свои мысли в устной форме; слушать и понимать речь других.

Познавательные УУД: умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную ранее на уроке.

Тип урока: изучение нового материала.

Оборудование: компьютер, проектор, интерактивная доска, циркуль, линейка, карандаш, предметы с круглым дном, нитка, микрокалькулятор.

Ход урока

1. Организационный момент.

На доске записано: “Вдохновение нужно в математике, как в поэзии”

Учитель: Здравствуйте, ребята! Как известно, математика – царица наук, одна из самых древнейших наук и в то же время очень интересная и очень нужная. Сегодня мы с вами убедимся в этом, и очень хочется, чтобы на этом уроке каждый из вас побывал в роли ученого, сделал свое маленькое открытие нового знания. Давайте улыбнемся друг другу и начнем плодотворную работу на уроке математики! (слайд 1)

2. Мотивация учебной деятельности.

Учитель: Название нашей темы урока состоит из двух слов. Первое слово вы узнаете, выполнив следующее задание:

1. Округлите число до заданного разряда, из предложенных вариантов выберете правильный ответ, каждому числу поставлена в соответствие буква, из букв составьте слово. (слайд 2)

Округлите :

6, 789 до десятых

0, 214 до целых

18, 25 до десятых

13, 141516 до тысячных

3, 1415 до сотых

Учитель: Получилось слово? Правильно - «Длина». (на экране появляется правильный ответ)

2. Отгадайте загадку и вы узнаете следующее слово темы: (слайд 3)

Если видишь солнце в небе, или чашку с молоком,

Видишь бублик или обруч, слышишь сказку с колобком,

В круглом зеркале увидел ты сейчас свою наружность.

И вдруг понял, что фигура называется …( окружность)

Учитель: Так какая тема сегодняшнего урока?

Ученики: «Длина окружности».

Учитель: Откройте тетради, запишите число и тему урока: «Длина окружности» (слайд 4)

Учитель: Как вы думаете, чему мы сегодня должны научиться?

Ученики: Сегодня мы должны:

 1) Повторить основные понятия темы «Окружность».

 2) Вывести формулу для вычисления длины окружности.

 3) Учиться применять эту формулу при решении задач.

3. Актуализация опорных знаний (фронтально).

Учитель: Давайте вспомним, что мы уже знаем про окружность? (слайд 5)

Работа по готовому чертежу.

Какая геометрическая фигура изображена на чертеже?(Это интересно: Впервые построением окружности занимался древнегреческий учёный – Аполлоний (260 - 170 г. до н. э. ))(слайд 6)

Весь материал - смотрите документ.

Конспект урока математики в 6 классе по теме "Длина окружности"

Учитель: Казакова Ольга Викторовна,

учитель математики и информатики

МОУ «Средняя общеобразовательная школа №1»

1. Цель урока: формирование практико-ориентированной компетенции при выведении формулы длины окружности и её применения при решении задач.

2. Задачи урока:

Образовательные:

• обеспечение усвоения учащимися формул по нахождению длины окружности;

• отработка навыков по применению данных формул при решении задач;

• усвоение учащимися понятий: длина окружности, число π.

• приобретение навыков исследовательской работы;

Развивающие:

• развитие у учащихся коммуникативных компетентностей (культуры общения, умения работать в группах);

• развитие практической направленности изучаемого материала;

• развитие математической речи, памяти, умения анализировать, обобщать и делать выводы;

• развитие познавательного интереса к предмету, логического мышления;

• развитие творческой и мыслительной деятельности учащихся, их интеллектуальных качеств;

 Воспитательные:

• воспитание прилежания, аккуратности, трудолюбия, чувства коллективизма, умения слушать и слышать;

• воспитание уважения и интереса к математике, умения видеть математические задачи в окружающем нас мире;

3. Формируемые универсальные учебные действия (УУД):

Личностные УУД: способность к самооценке на основе критерия успешности учебной деятельности.

Регулятивные УУД: умение определять и формулировать цель на уроке с помощью учителя; работать по коллективно составленному плану; оценивать правильность выполнения действий; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.

Коммуникативные УДД: умение оформлять свои мысли в устной форме; слушать и понимать речь других.

Познавательные УУД: умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную ранее на уроке.

4.Тип урока: изучение нового материала.

5.Оборудование: компьютер, проектор, интерактивная доска, циркуль, линейка, карандаш, предметы с круглым дном, нитка, микрокалькулятор.

6. Структура урока.

1. Организационный момент.

2. Мотивация учебной деятельности

3. Актуализация опорных знаний

4. Изучение нового материала

5. Физкультминутка

6. Первичное закрепление знаний.

7. Подведение итогов урока.

8. Информация о домашнем заданий.

7. УМК:

1. Учебник математики. 6 класс: учебн. для общеобразоват. учреждений/(Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С,И,Шварцбурд) – 21-е изд.,стер. – М.: Мнемозина,2013.

2. Математика.6 класс: поурочные планы (по учебнику Н.Я.Виленкина, В.И.Жохова, А.С.Чеснокова, С,И,Шварцбурда),1,2 полугодие.3-е изд.,перераб. И исправлен. / авт.-сост. Л.А.Тапилина. Т.Л.Афанасьева. – Волгоград: Учитель,2011

Ход урока

1. Организационный момент.

На доске записано: “Вдохновение нужно в математике, как в поэзии”

Учитель: Здравствуйте, ребята! Как известно, математика – царица наук, одна из самых древнейших наук и в то же время очень интересная и очень нужная. Сегодня мы с вами убедимся в этом, и очень хочется, чтобы на этом уроке каждый из вас побывал в роли ученого, сделал свое маленькое открытие нового знания. Давайте улыбнемся друг другу и начнем плодотворную работу на уроке математики! (слайд 1)

1. Мотивация учебной деятельности.

Учитель: Название нашей темы урока состоит из двух слов. Первое слово вы узнаете, выполнив следующее задание:

1. Округлите число до заданного разряда, из предложенных вариантов выберете правильный ответ, каждому числу поставлена в соответствие буква, из букв составьте слово. (слайд 2)

Округлите :

6,789 до десятых

0,214 до целых

18,25 до десятых

13,141516 до тысячных

3,1415 до сотых

Учитель: Получилось слово? Правильно - «Длина». (на экране появляется правильный ответ)

1. Отгадайте загадку и вы узнаете следующее слово темы: (слайд 3)

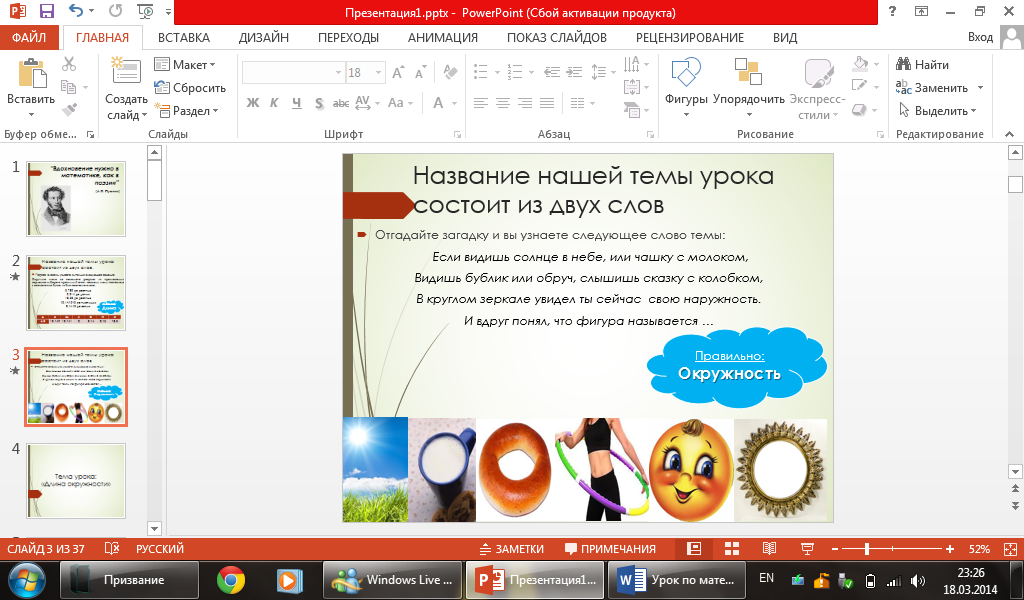
Если видишь солнце в небе, или чашку с молоком ,

Видишь бублик или обруч, слышишь сказку с колобком,

В круглом зеркале увидел ты сейчас свою наружность.

И вдруг понял, что фигура называется …( окружность)

Учитель: Так какая тема сегодняшнего урока?

Ученики: «Длина окружности».

Учитель: Откройте тетради, запишите число и тему урока: «Длина окружности» (слайд 4)

Учитель: Как вы думаете, чему мы сегодня должны научиться?

Ученики: Сегодня мы должны:

1) Повторить основные понятия темы «Окружность».

2) Вывести формулу для вычисления длины окружности.

3) Учиться применять эту формулу при решении задач.

1. Актуализация опорных знаний (фронтально).

Учитель: Давайте вспомним, что мы уже знаем про окружность? (слайд 5)

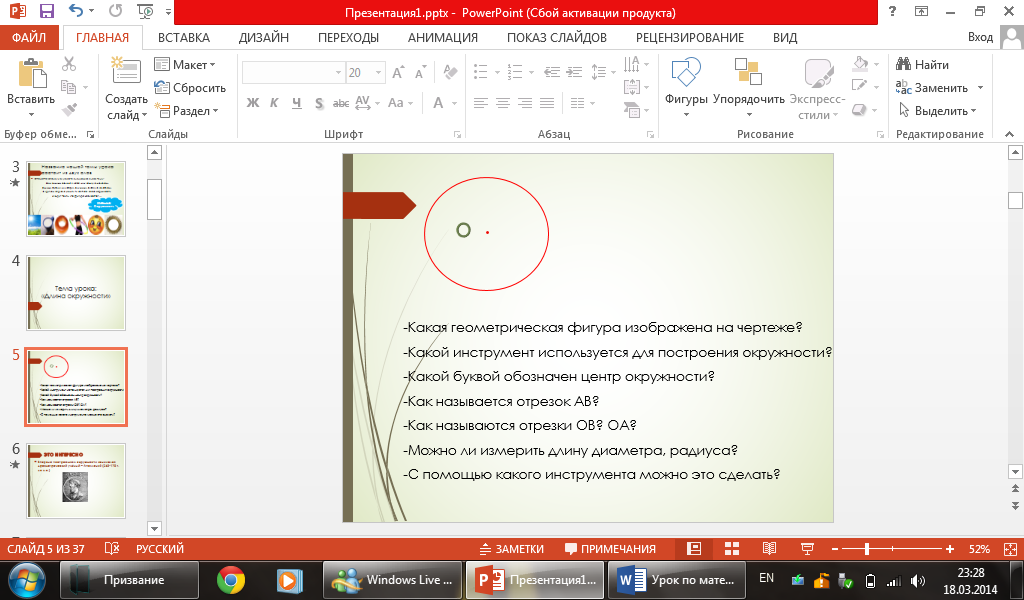
Работа по готовому чертежу. 

• Какая геометрическая фигура изображена на чертеже?(Это интересно: Впервые построением окружности занимался древнегреческий учёный – Аполлоний (260-170 г. до н.э.))(слайд 6)

• Какой инструмент используется для построения окружности? (слайд 7).

• Какой буквой обозначен центр окружности?

• Как называется отрезок АВ?

• Как называются отрезки ОВ? ОА?

• Можно ли измерить длину диаметра, радиуса?

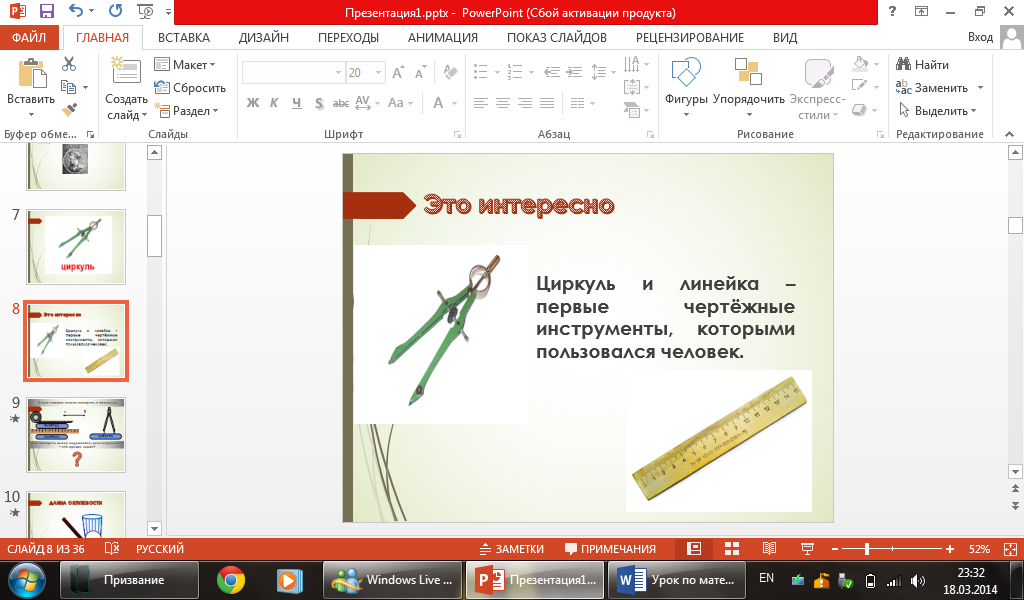
• С помощью какого инструмента можно это сделать? (Это интересно Циркуль и линейка – первые чертёжные инструменты, которыми пользовался человек).(слайд 8)

1. Изучение нового материала

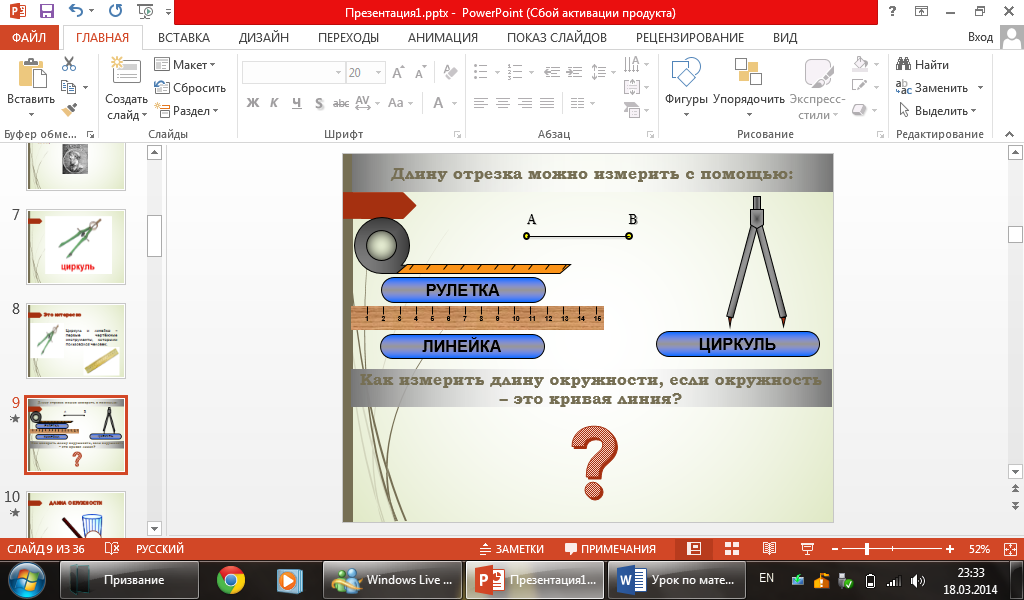
Учитель: Вы знаете, что длину отрезка можно измерить с помощью линейки. А как измерить длину окружности, если окружность – это кривая линия? Существует ли такой инструмент, с помощью которого можно это сделать? (слайд 9)

Для того, чтобы измерить длину окружности необходимо (слайд 10):

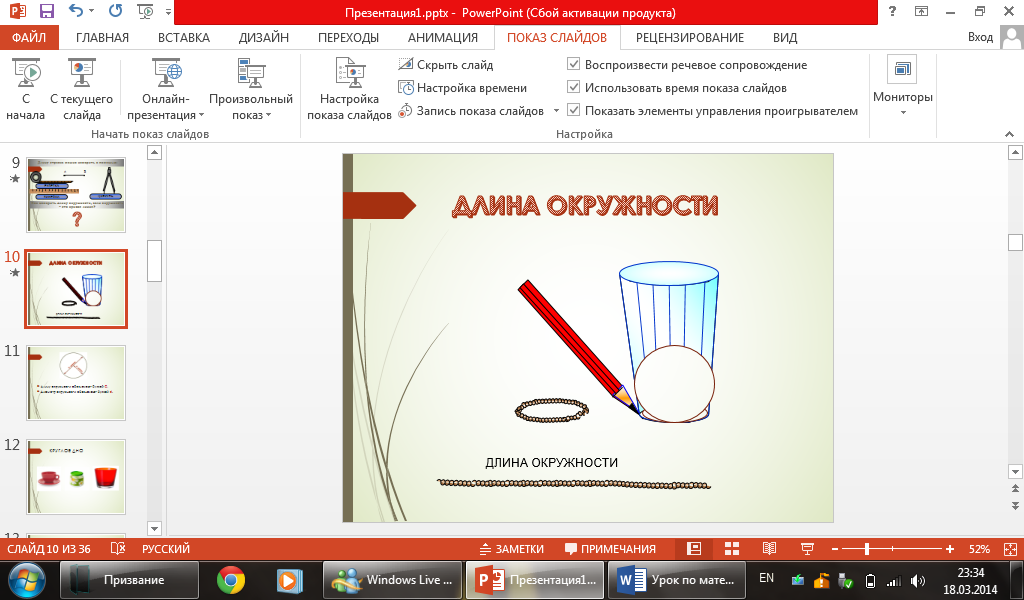
1. Взять предмет с круглым дном и обвести его дно карандашом в тетради.

2. Обернуть дно предмета ниткой так, чтобы концы нитки совпали в одной и той же точке окружности, оставшуюся часть нитки отрезать.

3. Выпрямить эту нитку и по линейке измерь ее длину, это и будет длина окружности.

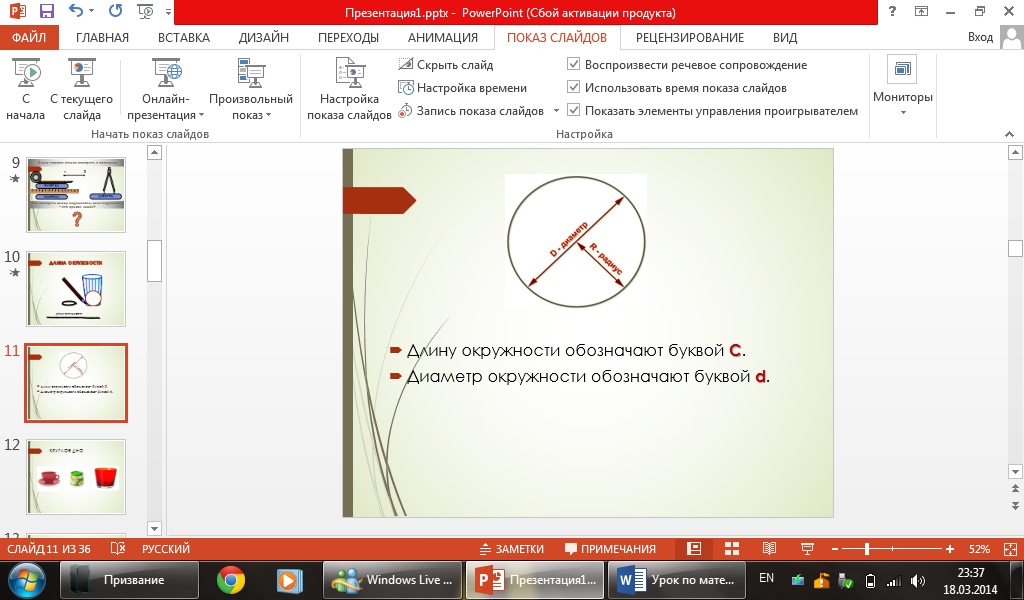
Длину окружности обозначают буквой С. Диаметр окружности обозначают буквой d (слайд 11).

Оказывается, что существует зависимость между длиной окружности и диаметром. Какая? Это мы сейчас установим, выполнив практическую работу в парах. У вас на столах лежат предметы с круглым дном разного диаметра (слайд 12).

Практическая работа «Нахождение длины окружности» (слайд 13).

Указание: (слайд 14)

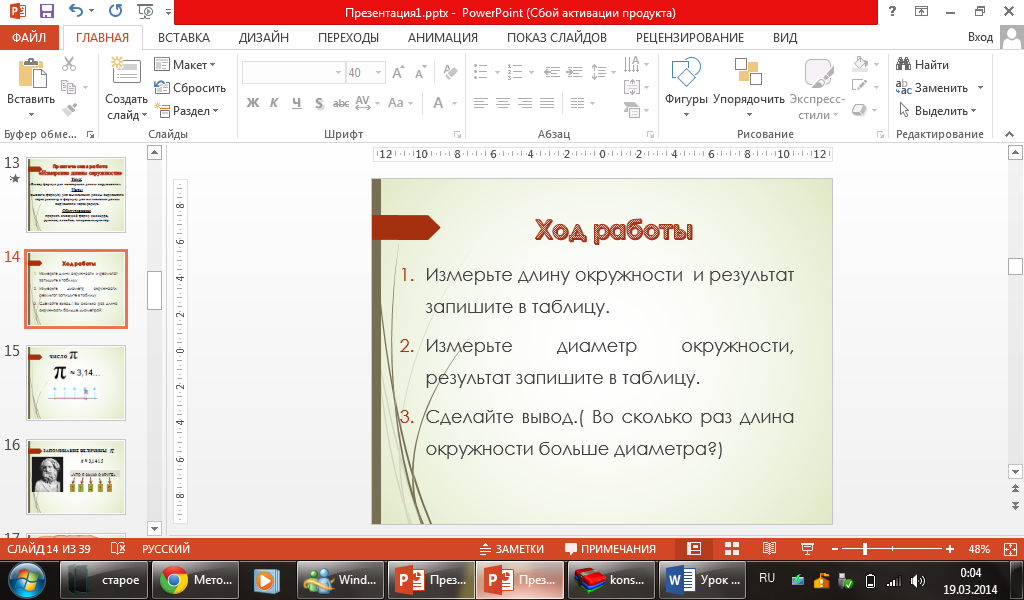
  1. Измерьте длину окружности  и результат запишите в таблицу.

  2. Измерьте диаметр окружности, результат запишите в таблицу.

1. Сделайте вывод. (Во сколько раз длина окружности больше диаметра?)

Учитель: (Анализ выполненной работы) Посмотрите на 3 столбик в таблице, где вы находили отношение длины окружности к ее диаметру. Что вы там видите?

Ученики: Результаты деления получились одинаковыми.

Учитель: Как вы думаете - это справедливо для всех окружностей?

Ученики: Да, так как у нас были предметы разные по размеру. А отношение длины окружности к длине ее диаметра является одним и тем же числом.
Учитель: Итак, давайте сформулируем вывод: Отношение длины окружности к длине диаметра всегда одно и то же число.

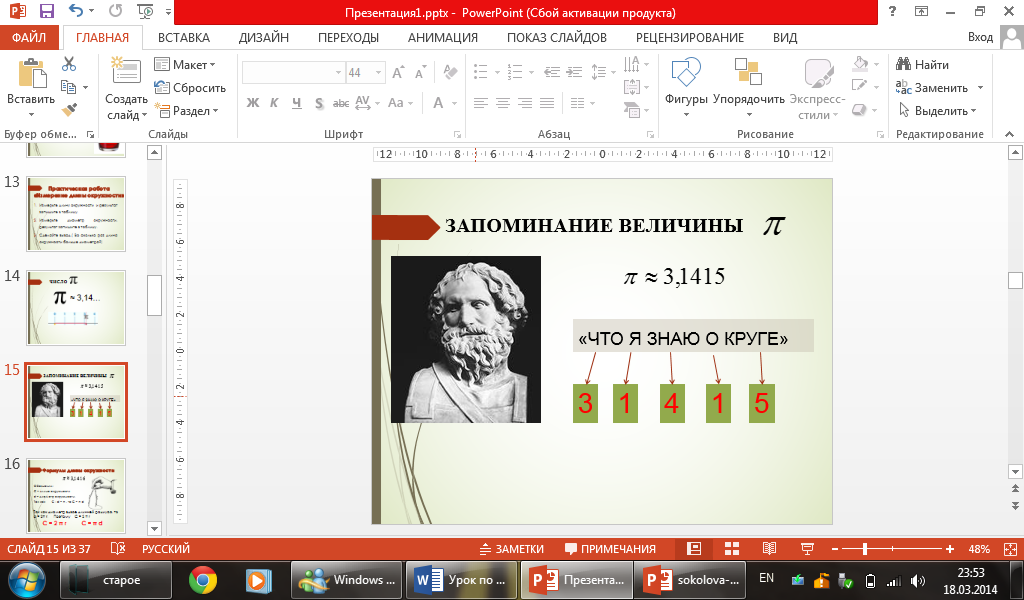
Учитель: Число, которое мы получили, обозначается греческой буквой π (читаем пи). Оно является бесконечной десятичной дробью, но для вычислений мы будем пользоваться его приближенным значением, равным 3,14 (слайд 15). π ≈ 3,1415926…

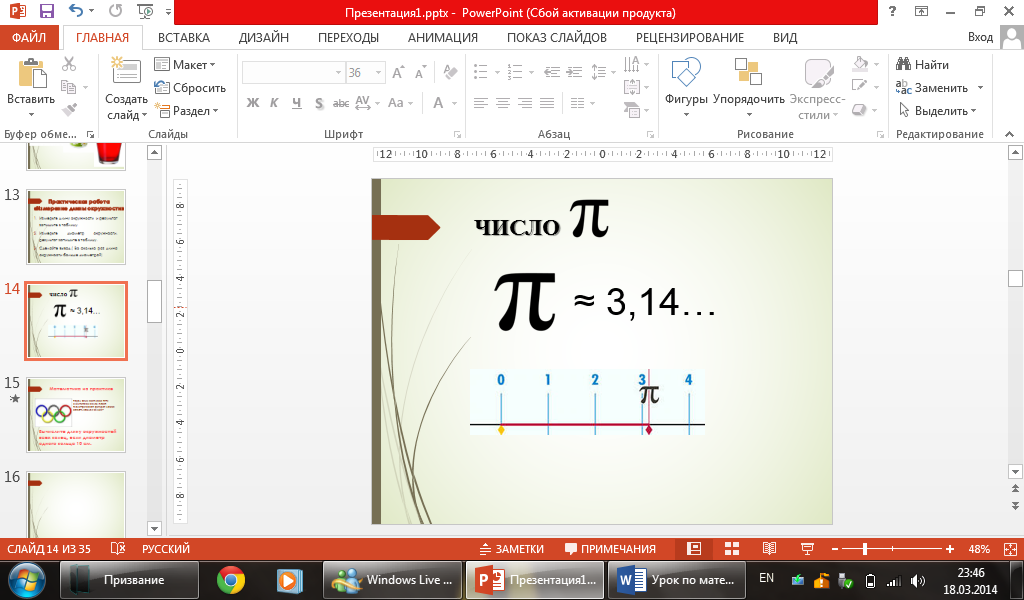
Запишите в тетрадь: π ~ 3,14.

Первые цифры этого числа можно запомнить по числу букв в каждом слове следующей фразы: «что я знаю о круге» (слайд 16)

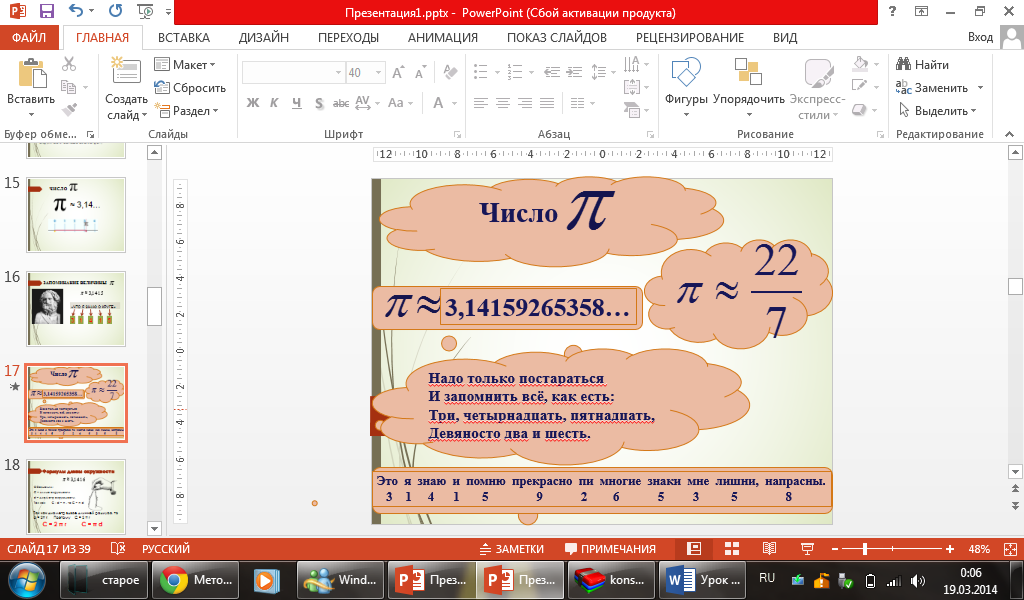
Для запоминания цифр числа π может пригодиться и такое четверостишие (слайд 17):

Надо только постараться

И запомнить всё как есть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Или:

Это  я  знаю  и  помню  прекрасно  пи  многие  знаки  мне  лишни,  напрасны.

   3    1     4     1       5               9           2        6           5         3        5               8

В этой фразе количество букв в словах позволяет восстановить последовательность начальных десятичных знаков числа π.

Учитель: Обратимся к исторической справке о числе π.

Ученик: В глубокой древности при строительстве сооружений человек сталкивался с проблемой нахождения длины окружности. В результате практических действий люди поняли, что отношение длины окружности к ее диаметру есть величина постоянная. Впервые обозначением этого числа греческой буквой  воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году. (слайд 18)

Учитель: Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.

Ученик: Дальнейшая история числа π  связана с его вычислением. Китаец Цзу Чунчжи в 5 веке нашел восемь правильных знаков. Голландец Людольф ван Цейлен вычислил 35 знаков. В 1706 году англичанин Джон Мечин впервые смог найти сто знаков π. В настоящее время находят миллионы знаков π  с помощью компьютеров (слайд 19).

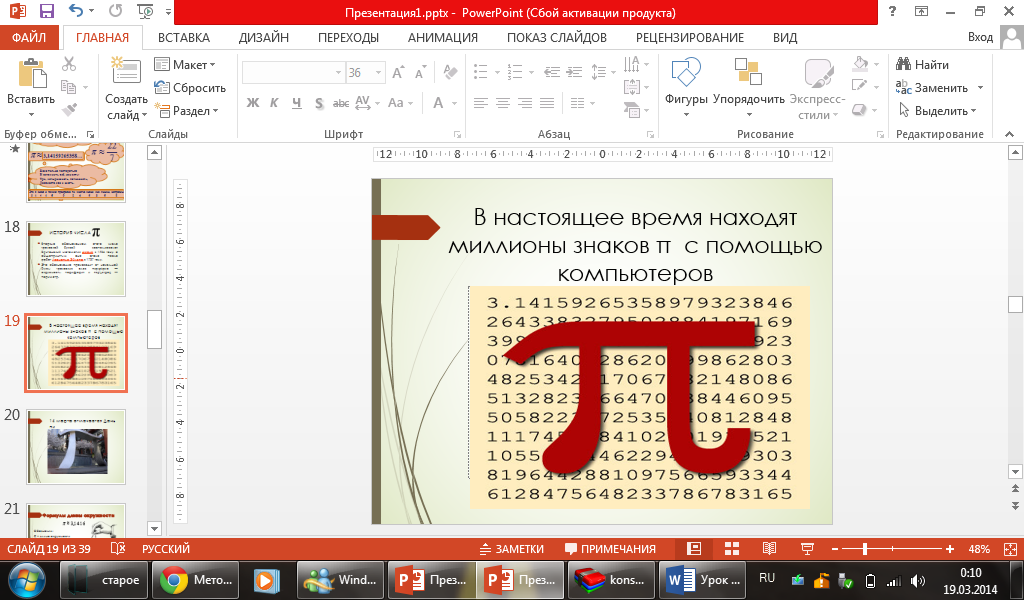
π  ≈3,141592653589793238462643…

Учитель: в расчетах используют π≈3,14

Ученик: 14 марта отмечается День пи- неформальный праздник математиков. «Отцом» праздника стал Лари Шоу, обративший внимание на то, что этот день приходится на 3.14 в американской системе записи дат. В Сиэтле установлена металлическая скульптура числа π (слайд 20).

Учитель: Ниткой удобно пользоваться для измерения длины окружности малого радиуса. А как быть, если требуется измерить длину окружности предмета круглой формы большого размера, например, бассейна или арены цирка? С помощью нитки и веревки это сделать можно, но весьма трудоемко и результат таких измерений может быть неточным. Поэтому мы должны подумать, как же вычислить длину окружности без ее измерений. Из практической работы мы выяснили, что (слайд 21)

С/d = π,

выразим длину окружности

С= π*d.

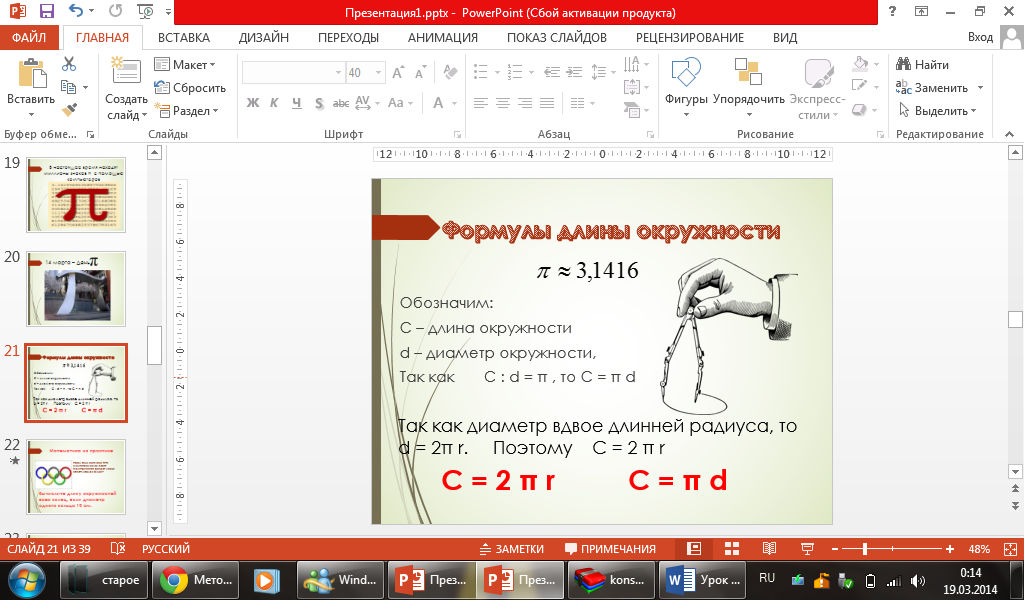
Учитель: Длина окружности равна произведению диаметра на число π.
А так как d=2r, то С =2 π r.

Учитель: С этого дня для нахождения длины окружности, мы будем пользоваться формулами С = π* d, С = 2* π*r., а для этого достаточно знать радиус или диаметр окружности. Запишите формулы в тетрадь и к следующему уроку вы должны их знать.

1. Физкультминутка. (слайд 22)

А теперь ребята встали

Быстро руки вверх подняли

В стороны, вперед, назад.

Повернулись влево, вправо

Тихо сели, вновь за дело.

1. Первичное закрепление знаний.

Решение задач у доски и в тетрадях.

Учитель: Не так давно закончилась зимняя олимпиада в Сочи. Перед вами сцепление пяти олимпийских колец. Какой геометрической фигурой можно назвать каждое кольцо? (слайд 23)

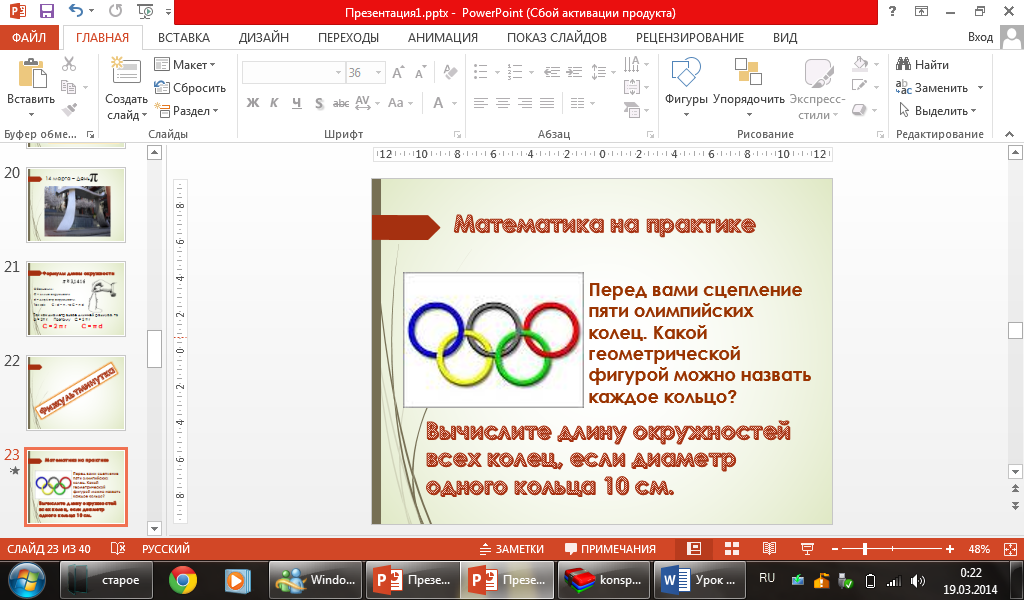
Ученики: Окружность.

Учитель: Вычислите длину окружностей всех колец, если диаметр одного кольца 10 см.

Решение.

d = 10 см;   3,1;

с = d  10*3,1  31 (см).- длина окружности одного кольца

31*5=155 (см)-длина окружностей 5 олимпийских колец

Ответ: 155 см.

Работа с учебником: (слайд 24)

1. Решить № 849 на доске и в тетрадях.

Решение.

d = 50 см;   3,1; с = d  50*3,1  135 (см).

Ответ: 135 см.

2. Решить № 847 (три человека решают на доске, остальные самостоятельно в тетрадях, потом проверяется решение).

3. Решить № 850 (выполнить необходимые измерения – измерить диаметр окружности).

Решение.

d = 2,8 см; r = 1,4 см; длина половины окружности равна

r = 1,4 · 3,14  4,396  4,4 (см).

Ответ: 4,4 см.

1. Подведение итогов (слайд 25)

Сегодня на уроке мы:

-Узнали…       (Новое число π Формулы, по которым вычисляется длина окружности).

-Научились…  (Решать задачи с помощью формулы длины окружности).

- А теперь продолжите предложения, которые вы видите на экране:

Сегодня я узнал…
Было интересно…
Теперь я могу…
Я научился…
У меня получилось

1. Домашнее задание: (слайд 26)

Изучить п. 24; решить № 868, 869, 863, найти ребусы и шутки о числе π.