Алгебра. 9 класс
Учебник. Алгебра. 9 классАвторы. Кузнецова Е.П., Муравьева Г.Л., Шнеперман Л.Б., Ящин Б.Ю.
Тема урока. Решение квадратных неравенств
Тип урока. Урок изучения нового материала с первичным закреплением знаний
Форма урока. Практикум
Цель урока. Формирование у учащихся умения решать квадратные неравенства по алгоритму.
Задачи урока.
Образовательные: создание условий для
актуализации опорных знаний по применению свойств квадратичной функции при решении неравенств, умению схематически строить график квадратичной функции, определению по графику промежутков знакопостоянства функции;
применения обобщённых знаний, умений и навыков в новых условиях – создание проблемной ситуации с целью показать внутрипредметные связи;
контроля и самоконтроля знаний, умений и навыков: средства –домашняя работа, самостоятельная работа.
Развивающие: создание условий для
развития логического мышления, умения работать в проблемной ситуации, умения применять преемственность тем математики;
развития умений сравнивать, обобщать, правильно переформулировать условие задачи, излагать мысли, делать выводы;
развития самостоятельной деятельности учащихся.
Воспитательные: создание условий для
воспитания интереса и любви к предмету через содержание учебного материала урока, методов обучения;
совершенствования умения работать в группе, культуры общения.
Оборудование: проектор, сигнальные карточки 2-х цветов, презентация, раздаточный материал (графическая работа, алгоритм решения квадратного неравенства, самостоятельная работа).
Ход урока.
Класс делится на группы (группы смешанного типа).
1. Мотивационно-целевой этап. (3 мин)
Дидактическая задача. Подготовить учащихся к работе на уроке, выразить задачи урока, выяснить ожидания учащихся.
1.1 Мотивация. Приветствие.
Тема сегодняшнего урока «Решение квадратных неравенств». Французская пословица гласит: «Знания, которые не пополняются ежедневно, убывают с каждым днём».
Чем же мы пополним сегодня наши знания?
1.2 Целеполагание.
Метод: импровизированные цели.
Фома работы: групповая
Учащимся сообщается тема урока . На доске размещается ватман, в середине которого в кругу записана тема урока «Решение квадратных неравенств». Вокруг изображены пустые овалы. Учащимся предлагается продумать и обсудить в группах задачи, над которыми будет проведена работа на уроке. Затем задачи озвучиваются, обсуждаются, наиболее значимые записываются в пустые овалы.
2. Этап проверки домашнего задания (1 мин)
Дидактическая задача. Установить правильность и осознанность выполнения всеми учащимися домашнего задания; устранить в ходе проверки обнаруженные пробелы знаниях, совершенствуя при этом ЗУН.
В течение перемены на доске были предложены решения упражнений домашнего задания. Учащиеся сверяют решения с эталонами, получают консультацию учителя (приложение 1).
На этапе проверки домашнего задания учитель еще раз делает акцент на вопросах и заданиях, вызвавших наибольшие затруднения у учащихся.
3. Этап актуализации опорных знаний и выявление места и причины затруднений. (7 минут)
Дидактическая задача. Подготовка мышления учащихся и организация осознания ими внутренней потребности к построению учебных действий и организация фиксирования каждым из них индивидуального затруднения.
Метод: графическая работа
Форма работы: индивидуальная
3.1 Учащиеся выполняют графическую работу по карточкам (приложение 2).
3.2 Обратная связь (метод светофор). Учащиеся осуществляют самопроверку по образцу. Фиксируют индивидуальные затруднения (приложение 3).
После проверки учащимся предлагается самим определить затруднения. Учитель определяет индивидуальные затруднения учащихся с помощью сигнальных карточек по пунктам: зеленая – нет затруднений, красная – имею затруднения.
Не знаю формулу дискриминанта квадратного уравнения
Делаю ошибки при вычислении
Не умею определять направления ветвей параболы
Не умею определять количество нулей квадратичной функции
Не умею определять количество промежутков знакопостоянства квадратичной функции
3.3 В целях коррекции проводится систематизация и обобщение знаний и умений в ходе фронтальной беседы (приложение 4).
4. Этап изучения нового материала
Дидактическая цель. Построение учащимися нового способа действий и первичного обобщения и систематизации новых знаний.
Метод. Частично-поисковый.
Форма работы: групповая, фронтальная
4.1 Вернемся к дополнительному заданию вашей домашней работы (приложение 5).
Упростим условие: определите промежутки знакопостоянства функции у=х2 +4х+3.
Для этого по-прежнему требуется график.
Проблемный вопрос: все ли этапы построения графика квадратичной функции необходимы для определения промежутков знакопостоянства функции? Обсудите в группах и определите номера пунктов, которые считаете лишними.
Ответ. Лишние пункты 2, 3, 5. То есть ось Оу не важна, не имеет значения вершина параболы и ось симметрии, а точки пересечения с осью Ох можно заменить нахождением нулей функции.
Вывод: для решения этого задания достаточно знать направление ветвей параболы и нули функции. Параболу можно строить схематично.
4.2. Изменим условие задания. Определите при каких значениях х функция у=х2 +4х+3 принимает положительные значения, то есть у0.
Обсудите решение в группах.
Ответ. Из промежутков знакопостоянства выбирают промежутки, на которых функция принимает положительное значение.
Ответ: у0 на промежутках (–∞;–3) и (–1;+∞)
4.3 Следующее задание: решите неравенство х2 +4х+30.
Обсудите условие этого задания в группах и сравните его с условием предыдущего упражнения.
Ответ: решения аналогичны. Разница в записи ответа.
4.4 Мы практически определили, по какому алгоритму решаются квадратные неравенства. Давайте приведем полученные знания в систему (приложение 6).
5. Этап первичной проверки усвоения знания. Контроль и самоконтроль знаний.
Дидактическая задача. Применение новых знаний в типовых заданиях. Определение степени усвоения учащимися алгоритма решения квадратного неравенства, выявление затруднений учащихся. Самооценка учащимися результатов своей деятельности.
Метод: самостоятельная работа
Форма работы: индивидуальная
- А теперь проверим, насколько хорошо вы усвоили алгоритм. Вам предлагается решить три неравенства. В целях экономии времени можно пользоваться результатами графической работы (учащиеся получают карточки с заданиями) (приложение 7).
Обратная связь (метод светофор). Учащиеся сверяют решения с эталоном (приложение 8).
После проверки учащимся предлагается самим определить собственные затруднения. Учитель определяет индивидуальные затруднения учащихся с помощью сигнальных карточек по пунктам: зеленая – нет затруднений, красная – имею затруднения.
Не знаю формулу дискриминанта квадратного уравнения
Делаю ошибки при вычислении
Не умею определять направления ветвей параболы
Не умею определять количество нулей квадратичной функции
Не умею определять количество промежутков знакопостоянства квадратичной функции
Испытываю затруднения при схематическом изображении параболы
Испытываю затруднения при определении знака в каждом из промежутков
Испытываю затруднения при записи решения неравенства (ответа)
Иные затруднения _____________________________________________
6. Физкультминутка
Метод «Земля, воздух, огонь и вода»
Задача этапа: снятие эмоционального и физического напряжения.
Учитель просит обучающихся по его команде изобразить одно из состояний – воздух, землю, огонь и воду.
Воздух. Ученики начинает дышать глубже, чем обычно. Они встают и делают глубокий вдох, а затем выдох. Каждый представляет, что его тело, словно большая губка, жадно впитывает кислород из воздуха. Все стараются услышать, как воздух входит в нос, почувствовать, как он наполняет грудь и плечи, руки до самых кончиков пальцев; как воздух струится в области головы, в лицо; воздух заполняет живот, область таза, бедра, колени и стремится дальше – к лодыжкам, ступням и кончикам пальцев. Ученики делают несколько глубоких вдохов и выдохов. Можно предложить всем пару раз зевнуть. Сначала это получается скорее искусственно, но иногда после этого возникает настоящий зевок. Зевота – естественный способ компенсировать недостаток кислорода. (Зевание может использоваться и по-другому: вы можете на первой встрече предложить зевать сознательно, чтобы группа быстрее «взбодрилась»).
Земля. Теперь ученики должны установить контакт с землей, «заземлиться» и почувствовать уверенность. Учитель вместе с обучающимися начинает сильно давить на пол, стоя на одном месте, можно топать ногами и даже пару раз подпрыгнуть верх. Можно потереть ногами пол, покрутиться на месте. Цель – по-новому ощутить свои ноги, которые находятся дальше всего от центра сознания, и благодаря этому телесному ощущению почувствовать большую стабильность и уверенность.
Огонь. Ученики активно двигают руками, ногами, телом, изображая языки пламени. Учитель предлагает всем ощутить энергию и тепло в своем теле, когда они двигаются подобным образом.
Вода. Эта часть упражнения составляет контраст с предыдущей. Ученики просто представляют себе, что комната превращается в бассейн, и делают мягкие, свободные движения в «воде», следя за тем, чтобы двигались суставы – кисти рук, локти, плечи, бедра, колени.
7 этап. После проведения самопроверки класс делится на 2 группы.
Учащиеся, успешно справившиеся с самостоятельной работой (1 группа), выполняют задания по отработке навыка решения квадратных неравенств и применения знаний в новой ситуации.
Учащиеся, допустившие ошибки работают фронтально под руководством учителя (2 группа). Учащиеся пересаживаются по группам.
| 1 группа | 2 группа |
| Этап выполнения упражнений с переносом знаний в новые условия. Дидактическая задача: отработка навыка решения квадратных неравенств, формирование умения применения знаний в новой ситуации Форма работы: индивидуальная | Этап коррекции знаний. Дидактическая задача: выработка умений безошибочно применять знания. Форма работы: фронтальная
|
| Работа с учебником. № 2.20 (7) (неравенство с отрицательным дискриминантом), № 2.29 (1) (неравенство с дискриминантом равным нулю) № 2.41 (3) | Работа с учебником. № 2.17(5) (неравенство с отрицательным дискриминантом), № 2.27 (5) (неравенство с дискриминантом равным нулю) № 2.35 (1) |
| Учащиеся выполняют самопроверку по ответам. Сдают тетради на проверку учителю. | После проведения работы учащиеся еще раз возвращаются к определению своих затруднений. Определяют круг вопросов требующих доработки. Учитель отслеживает приращения в знаниях. |
| Д/з 2.20 (8); 2.29 (4); 2.41 (5) | Д/з 2.18 (5); 2.28 (1); 2.35 (2) |
8. Информация о домашнем задании.
| 1 группа | 2 группа |
| Д/з 2.20 (8); 2.29 (4); 2.41 (5) | Д/з 2.18 (5); 2.28 (1); 2.35 (2) |
9. Подведение итогов урока. Рефлексия
Дидактическая задача: самооценка учащимися результатов своей деятельности, осознание метода построения и границ применения нового способа действия.
Метод: эвристическая беседа
Форма работы: фронтальная
Отметки выставляются учащимся по желанию с учетом выполнения двух письменных работ.
Рефлексия в форме эвристической беседы.
1. Что вы ожидали от урока и что получилось?
2. Какие этапы урока вы считаете наиболее удачными и почему?
3. Какие события (действия, мнения и т.п.) вызвали наиболее яркие ощущения?
4. Была ли польза от такого рода работы?
5. В чем вы видите собственное приращение?
6. Перечислите в порядке убывания основные проблемы и трудности, которые вы испытывали во время урока. Какими способами вы их преодолевали?
7. Что мы делали нерационально? Назовите одно действие, которое можно добавить, чтобы завтра сделать нашу работу на уроке более успешной.
8. Что и почему можно изменить в нашей работе?
Приложение 1
№ 2.8
| 2. х2+4≥0. Так как х2≥0 при любых значениях х, то выражение х2+40. хє (–∞;+∞) Ответ: (–∞;+∞) | 3. – 9– х20; – х29; х2 так как х2≥0 при любых значениях х, то неравенство – 9– х20 не имеет решений. Ответ: нет решений |
№ 2.9
| 2. х2≤64; │х│≤8; – 8≤х≤8 хє[–8; 8] Ответ: [–8; 8] | 3. х2225; │х│15;
хє (–∞;–15) U (15;+∞) Ответ: (–∞;–15) U (15;+∞) |
Дополнительное задание.
Построить график функции у=х2 +4х+3 и определить промежутки знакопостоянства.
Решение.
у=х2 +4х+3
1. а =10, ветви параболы направлены вверх.
2. (хо; уо) – координаты вершины параболы.
хо=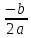 =
=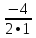 = –2
= –2
уо=(–2)2+4 (–2)+3=–1
(–2)+3=–1
(–2; –1)
3. х=–2 – ось симметрии параболы
4. Точки пересечения параболы с осью Ох:
х2 +4х+3=0
D=b2 –4ac =42 –4 1
1 3= 4 0
3= 4 0
х1=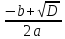 =
= 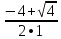 =–1
=–1
х2=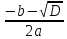 =
= 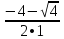 =–3
=–3
(–1;0) и (–3;0)
5. Точки пересечения параболы с осью Оу:
у(0)=с=3
(0; 3)
6. у0 на промежутках (–∞;–3) и (–1;+∞);
у
Приложение 2
1. Найдите дискриминант квадратного уравнения
| Уравнение | D |
| х2+х+2=0 | D= |
| 4х2-4х+1=0 | D= |
| –х2+5х-6=0 | D= |
2. Напротив правильных утверждений поставьте знак «+», воспользовавшись результатами № 1
| ФУНКЦИЯ | Ветви параболы направлены вверх | Ветви параболы направлены вниз | Функция имеет два нуля | Функция имеет один нуль | Функция не имеет нулей | Функция сохраняет знак на всей области определения | Функция имеет два промежутка знакопостоянства | Функция имеет трипромежутказнакопостоянства |
| у=х2+х+2 |
|
|
|
|
|
|
|
|
| у=4х2-4х+1 |
|
|
|
|
|
|
|
|
| у=–х2+5х-6 |
|
|
|
|
|
|
|
|
Затруднения.
Не знаю формулу дискриминанта квадратного уравнения
Делаю ошибки при вычислении
Не умею определять направления ветвей параболы
Не умею определять количество нулей квадратичной функции
Не умею определять количество промежутков знакопостоянства квадратичной функции
Приложение 3
Найдите дискриминант квадратного уравнения
уравнение
D
х2+х+2=0
D= b2 –4ac =12 –4
 1
1 2= -7 0
2= -7 04х2-4х+1=0
D= b2 –4ac =(-4)2 –4
 4
4 1= 0
1= 0–х2+5х-6=0
D= b2 –4ac =52 –4
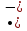 1)
1) (-6) = 1 0
(-6) = 1 0Напротив правильных утверждений поставьте знак «+», воспользовавшись результатами № 1
| ФУНКЦИЯ | Ветви параболы направлены вверх | Ветви параболы направлены вниз | Функция имеет два нуля | Функция имеет один нуль | Функция не имеет нулей | Функция сохраняет знак на всей области определения | Функция имеет два промежутка знакопостоянства | Функция имеет три промежутка знакопостоянства |
| у=х2+х+2 | + |
|
|
| + | + |
|
|
| у=4х2-4х+1 | + |
|
| + |
|
| + |
|
| у=–х2+5х-6 |
| + | + |
|
|
|
| + |
Приложение 4
1. ax2+bx+c=0
D = b2 – 4ac
2. y= ax2+bx+c – график парабола
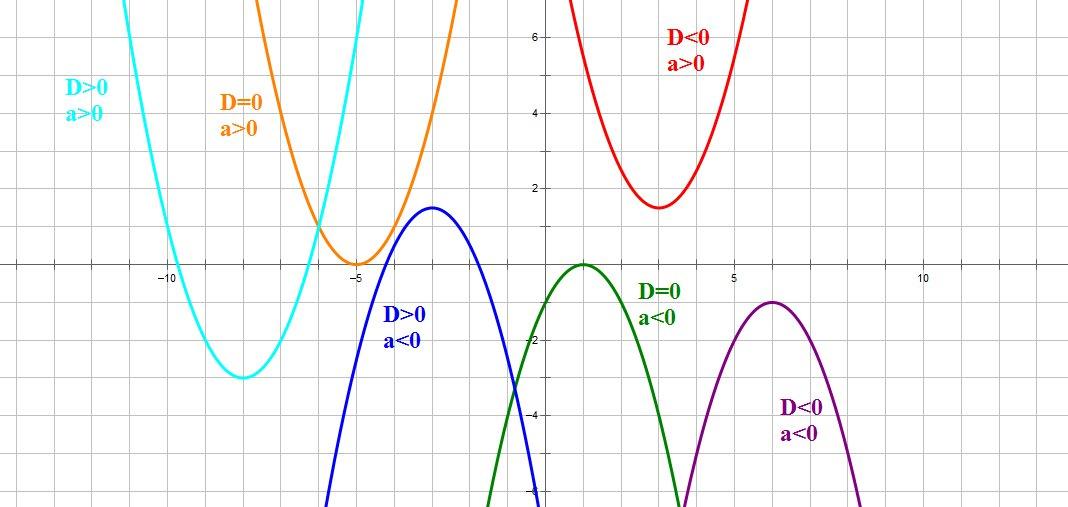
а0, ветви параболы направлены вверх(голубая, оранжевая и красная параболы)
а
3. D0, функция имеет 2 нуля и три промежутка знакопостоянства (голубая и синяя параболы)
D=0, функция имеет 1 нуль и два промежутка знакопостоянства (оранжевая и зеленая параболы)
D
Приложение 5
Решите неравенство х2 +4х+30
Решение.
1. Рассмотрим функцию у=х2 +4х+3
2. а =10, ветви параболы направлены вверх.
3. Нули функции:
х2 +4х+3=0
D=b2 –4ac =42 –4 1
1 3= 4 0
3= 4 0
х1=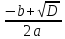 =
= 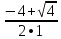 =–1
=–1
х2=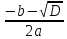 =
= 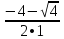 =–3
=–3
4. хє (–∞;–3) U (–1;+∞)
Ответ: (–∞;–3) U (–1;+∞)
Приложение 6
|
| Шаги решения квадратных неравенств aх2 +bх+c0 aх2 +bх+c aх2 +bх+c≥0 aх2 +bх+c≤0 | На что обращать внимание |
| 1 | Рассмотреть функцию у=aх2 +bх+c |
|
| 2 | Определим направление ветвей параболы | а0, ветви параболы направлены вверх а |
| 3 | Определим нули функции. aх2 +bх+c=0 D= b2 –4ac х1= х2= | D0, 2 нуля, три промежутка знакопостоянств D=0, 1 нуль, два промежутка знакопостоянств D |
| 4 | Отмечаем нули функции на оси Ох | Точки светлым кружочком, если знак неравенства или Точки черным кружочком, если знак неравенства ≥ или ≤ (неравенство нестрогое) |
| 5 | Схематически строим параболу |
|
| 6 | Знаками «+» и «-» отмечаем промежутки знакопостоянства функции | Парабола выше оси Ох – «+» Парабола ниже оси Ох – «-» |
| 7 | В ответ включаем промежутки, соответствующие знаку неравенства. | ; ≥ – знак «+» ≥; ≤ – нули функции включаются в ответ, скобки квадратные ; При записи ответа, состоящего из двух промежутков использовать знак U |
Приложение 7
Решите неравенство:
1) х2+х+2
2) 4х2-4х+10;
3) –х2+5х-6≥0.
После выполнения проверки обведите номера тех затруднений, которые вы испытываете:
Не знаю формулу дискриминанта квадратного уравнения
Делаю ошибки при вычислении
Не умею определять направления ветвей параболы
Не умею определять количество нулей квадратичной функции
Не умею определять количество промежутков знакопостоянства квадратичной функции
Испытываю затруднения при схематическом изображении параболы
Испытываю затруднения при определении знака в каждом из промежутков
Испытываю затруднения при записи решения неравенства (ответа)
Иные затруднения _____________________________________________
Приложение 8
| 1) х2+х+2 1. Рассмотрим функцию у= х2+х+2 2. а =10, ветви параболы направлены вверх. 3. Нули функции: х2 +4х+3=0 D= -7 Функция не имеет нулей 4. нет решений Ответ: нет решений | 1) 4х2-4х+10 1. Рассмотрим функцию у=4х2-4х+1 2. а =40, ветви параболы направлены вверх. 3. Нули функции: 4х2-4х+1=0 D= 0 х= 4. х є (–∞; Ответ: (–∞; | 1) –х2+5х-6≥0 1. Рассмотрим функцию у=–х2+5х-6 2. а =- 1 3. Нули функции: –х2+5х-6=0 D=10 х1= х2= 4. х є [2; 3] Ответ: [2; 3]
|

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок алгебры в 9классе. Решение квадратных неравенств (115.19 KB)
Урок алгебры в 9классе. Решение квадратных неравенств (115.19 KB)
 0
0 404
404 21
21 Нравится
0
Нравится
0



