Подготовка к экзаменам.
В Платошинской школе я работаю тридцать лет, имею шесть выпусков. Математике обучаю с пятого по одиннадцатый классы. За последние пять лет подготовить учащихся 9-х и 11-х классов к сдаче ГИА по математике мне довелось несколько раз.
Результаты были следующие:
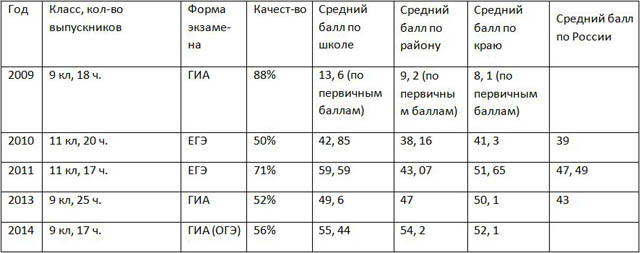
Специфика экзаменов в форме теста ставит ребят в довольно сложное положение, так как они должны оперировать своими знаниями и уметь применять их чаще всего в нестандартной для них ситуации. Вот здесь для меня и встает вопрос – «Как учить результативно, чтобы экзамен по математике стал проверкой знаний учеников?».
При этом многие действия учащихся при решении задач должны быть доведены до автоматизма. Для подготовки к сдаче государственных экзаменов необходимо повторить не только материал курса алгебры и начал анализа, но и некоторые из тем и разделов курса математики основной и средней школы. Встает еще один вопрос: «Как же подготовить учащихся к сдаче экзамена?». Ведь практически каждый день на уроке я слышу: «А я забыл, как делать... ».
Что делать в данной ситуации? Можно обратиться к помощи ребят или самой подсказать решение, но даже и после выполнения задания по всем правилам нет гарантии, что учащийся, столкнувшись с типичной проблемой в следующий раз, справится с ней самостоятельно.
Предупреждение и ликвидация пробелов в знаниях – одна из важнейших составляющих нашей работы, и неудовлетворительное качество этой работы ведет к накоплению у учащихся пробелов в знаниях до той степени, когда их устранение становится для ученика практически невозможным, и он переходит в разряд стабильно неуспевающих.
В этом случае о качественной подготовке к экзамену и говорить не приходится.Без целенаправленной работы по ликвидации пробелов даже самые строгие проверка домашних заданий и учительский контроль теряют смысл, а работа над ошибками мало соответствует своей цели.
Проблема «умения научить» очень сложная. Начать подготовку к экзаменам надо с правильной организации времени. Соблюдать все режимные моменты. Если позволяет время, нужно стремиться сделать повторение распределенным по времени, а не концентрированным. Именно поэтому мы, учителя, всегда советуем ребятам начинать повторение за несколько месяцев до экзаменов. Если ученик повторит материал несколько раз на протяжении всего года, то это даст гораздо более высокий результат.
Для успешного изучения материала, я поняла очень важный момент, что надо правильно ставить цели, для его запоминания. Именно от мотивации зависит продуктивность запоминания. Если ученик запоминает материал с установкой, что эта информация понадобится в скором времени, то материал усваивается быстрее, помнится дольше, воспроизводится точнее.
Экзамен по математике - это итог работы и ученика, и учителя на протяжении всего обучения в школе, и подготовка к нему является важной составляющей учебного процесса. И от того, насколько грамотно построен будет учебный процесс, зависит наш результат.
У меня сложилась определенная система подготовки учащихся к итоговой аттестации. Поэтому я начинаю целенаправленно готовить учащихся к такому виду экзамена еще с 5 класса, введя тестовые задания в работы учащихся.
В начале каждого учебного года в 5-9 классах провожу входные мониторинговые контрольные работы для выявления остаточных знаний учащихся. При этом учащиеся знают, что по мере усвоения материала они могут переходить в следующую по уровню подготовки группу. В 6 классе учащиеся должны хорошо усвоить тему с положительными и отрицательными числами, в 7 классе хорошо изучить формулы сокращенного умножения, в 8 классе решение квадратных уравнений.
Это глобальные темы, которые нельзя запускать. В целях оперативного контроля усвоения алгоритма очень часто провожу небольшие самостоятельные работы, цель которых – не выставление оценок, а выявление тех учащихся, которые что-то не поняли. Этим ребятам оказывается оперативная помощь консультантами.
При организации работы в группах, часть учащихся получает задания, направленные на достижение обязательных результатов обучения, причём, некоторые имеют перед собой образец выполнения задания, а другие – только алгоритм, более сильные учащиеся получают задания на продвинутом уровне.
На таком уроке моя работа сосредоточена на более слабых учениках. В сильной группе, как правило, всегда коллективными усилиями находят верное решение, самостоятельно применяя знания и приёмы деятельности в новой ситуации.
Оценивая учащихся, не спешу выставлять оценки в журнал, всегда даю возможность получить более высокую отметку и обязательно поправить «двойку». Для этого ученик должен сделать работу над ошибками самостоятельно или с помощью консультантов (с моей помощью), а затем решить аналогичное задание на уроке. Главное, что со временем ребята перестают бояться "двоек”, смелее задают вопросы, справляются с задачами обязательного уровня.
Обстановка на уроке доброжелательная, спокойная. Обучение алгоритмам даёт возможность достичь обязательного уровня обучения наиболее слабым учащимся и не может привести стандартизации мышления и подавлению творческих сил детей, так как выработка различных автоматизированных действий (навыков) – необходимый компонент творческого процесса, без них он просто невозможен.
Обучение алгоритмам не сводится к их заучиванию, оно предполагает и самостоятельное открытие, построение и формирование алгоритмов, а это и есть творческий процесс.
В 8-11 классах систематически провожу углублённую факультативную работу по предмету. Веду элективные курсы: в 8 классе «Алгебра модуля» - 16 ч, в 9 классе «Секреты процентов» - 18 ч, «Решение систем линейных уравнений (метод Гаусса, метод Крамера) » - 16 ч, «Элементы статистики и теории вероятностей» - 16 ч, в 10 - 11 кл. «Решение уравнений и неравенств с параметрами» - 34ч, «Решение уравнений и неравенств с модулем» - 34 ч, «Эленты статистики и теории вероятностей» - 18 ч. Программы курсов рассматривают ключевые и сложные темы школьной математики, помогают расширить спектр задач, посильных для учащихся и реализовать принципы дифференцированного обучения.
Для того чтобы увидеть уровень подготовленности выпускников к сдаче экзамена, ежемесячно в школе проводим тестирование по текстам тренировочных или диагностических работ системы СтатГрад. Технология проведения пробного тестирования максимально приближена к условиям проведения экзамена. После проверки второй части ученических работ заполняю форму отчёта в Excel, компьютер автоматически показывает протокол результатов тестирования.
Затем делаю анализ выполнения работ, что позволяет мне увидеть «пробелы учеников». На основании этого корректирую тематический план консультаций. Опыт свидетельствует о том, что такая организация деятельности позволяет выпускникам регулировать темп своей работы над тестом, снижает уровень тревожности перед экзаменом, вселяет веру в свои силы, позволяет адаптироваться в условиях аттестации.
По желанию школьников работу по устранению пробелов я провожу и во внеурочное время на специально организованных дополнительных занятиях. Время пребывания на этих занятиях для разных учащихся разное. Оно определяется количеством пробелов и успешностью их устранения. Так, ученику, не составит большого труда повторить материал и выполнить задания, в противном случае его бездействие регистрируется отрицательной оценкой. Хотя, как правило, до этого не доходит: ученик понимает, без ликвидации пробела он не сможет работать по данной теме результативно. Это позволяет включить в работу каждого ученика, не принуждая его, убеждая принять то содержание, которое заложено наукой.
Построение технологии обучения математике на основе индивидуальных особенностей и учёта целей развития каждого ребёнка способствует не только повышению качества знаний учащихся, но и их саморазвитию, самореализации, что является одной из важнейших целей современного образования.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Материал для учителей математики "Роль педагога в формировании результатов внешней оценки деятельности системы образования (ГИА)" (79 КB)
Материал для учителей математики "Роль педагога в формировании результатов внешней оценки деятельности системы образования (ГИА)" (79 КB)
 0
0 792
792 32
32 Нравится
0
Нравится
0


