Решение неравенств с двумя переменными

Решение неравенств

с двумя переменными

9 класс

Автор:

Сидорова А.В.

МБОУ СОШ № 31

Г. Мурманска

Устная работа

• 1. Какие из следующих чисел: –2; –1; 0; 2; 3 – являются решением неравенства х 3 – 2 х ≥ 1?
• 2. Подберите два каких-нибудь числа разных знаков, чтобы их сумма была больше 5.
• 3. Является ли пара чисел х = 2, у = 5 решением неравенства: 2 х 2 – у

Определение

• Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.

Определение

• Линейным неравенством с двумя переменными называется неравенство вида ах + by с, где х и у — переменные, а, b и с - некоторые числа.

Пример 1.

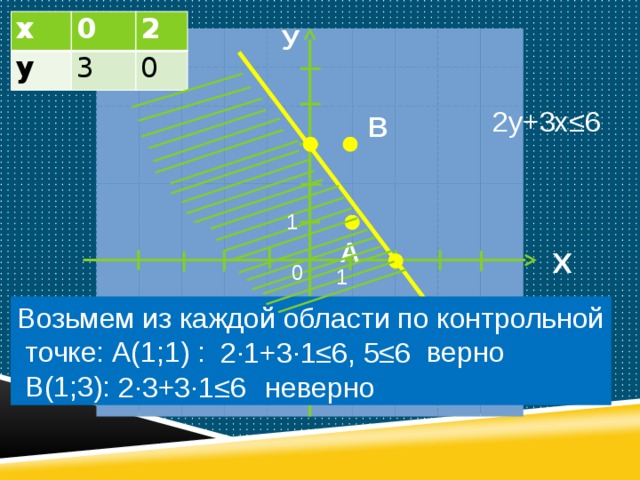
• Изобразим на координатной плоскости множество решений неравенства 2у+3х≤6.
• Решение.
• Строим прямую 2у+3х=6

у=3-1,5х

х

у

0

2

3

0

х

у

0

2

3

0

У

2у+3х≤6

B

1

A

Х

0

1

Возьмем из каждой области по контрольной

точке: А(1;1) :

В(1;3):

верно

2·1+3·1≤6, 5≤6

неверно

2·3+3·1≤6

ПЛАН ВЫПОЛНЕНИЯ ЗАДАНИЯ

• Заменить знак неравенства на равно.
• Выразить переменную у через переменную х.
• Построить график полученного

уравнения.

• Выбираем любую из полученных областей и рассматриваем в ней произвольную точку.
• Подставляем координаты точки в

неравенство.

• Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка.
• Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.

Пример 2.

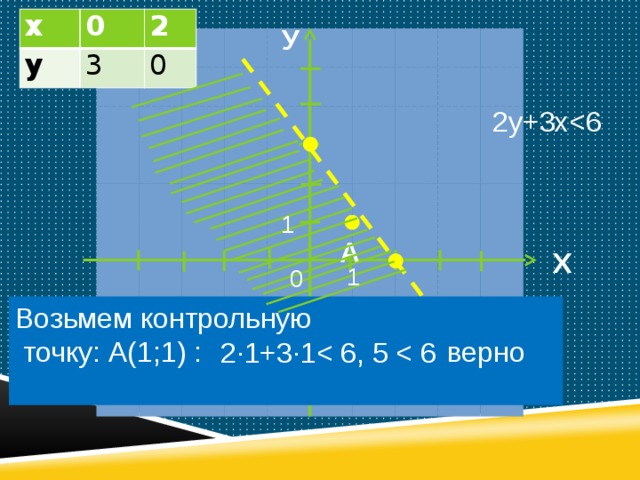
• Изобразим на координатной плоскости множество решений неравенства 2у+3х
• Решение.
• Строим прямую 2у+3х=6

у=3-1,5х

х

у

0

2

3

0

У

2у+3х

1

A

Х

1

0

Возьмем контрольную

точку: А(1;1) :

верно

2·1+3·1

Пример 3

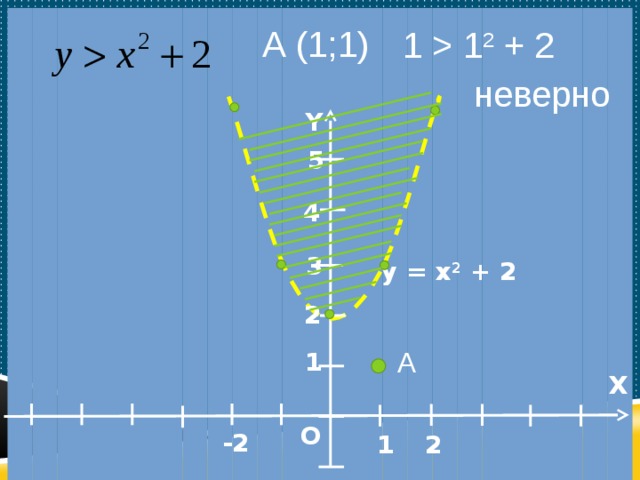
Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству

Выполняем задание по плану.

1 2 + 2 неверно Y 5 4 3 y = x 2 + 2 2 A 1 X O -2 2 1 " width="640"

А (1;1)

1 1 2 + 2

неверно

Y

5

4

3

y = x 2 + 2

2

A

1

X

O

-2

2

1

Задание 3.

Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству

х 2 + y 2

План выполнения задания

1. Заменить знак неравенства на равно:

х 2 + y 2 = 16

2. Определить, какая фигура задаётся таким уравнением:

х 2 + y 2 = 16 – уравнение окружности, с центром в начале координат, R = 4.

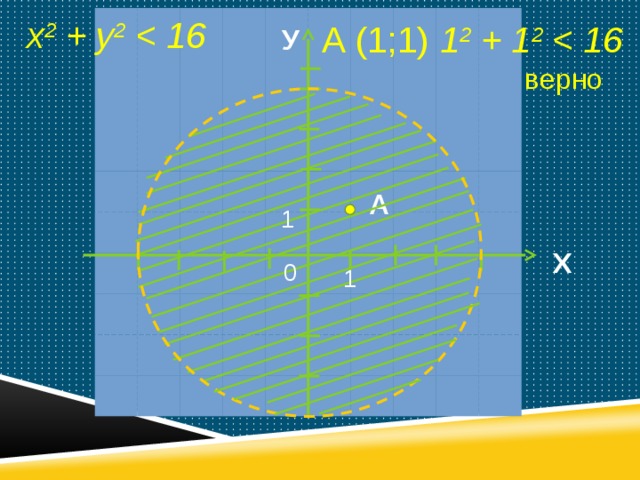
х 2 + y 2

1 2 + 1 2

А (1;1)

У

верно

A

1

Х

0

1

СПАСИБО за

внимание !