Пояснительная записка
В настоящее время в школах изучается единый предмет – математика, состоящий из двух предметных линий: алгебра и геометрия. На весь курс отводится 170 часов в год, из них 102ч. – алгебра; 68ч. – геометрия. Количество часов в неделю: 3 ч.- алгебры и 2 ч.- геометрии.
Для удобства работы и наглядности разработана данная форма рабочей программы. При составлении использовались примерные учебные программы, предложенные авторами учебников (Ю.Н. Макарычев и Л.С.Атанасян).
Предметная линия по алгебре для 9го класса
Рабочая программа предметной линии по алгебре для 9класса разработана на основе Примерной программы основного общего образования (базовый уровень) с учетом требований федерального компонента государственного стандарта общего образования и в соответствии с авторской программой Ю. Н. Макарычева. Данная рабочая программа рассчитана на 102учебных часа в том числе контрольных работ -8.
Используется учебно-методический комплект:
Макарычев Ю. Н. Алгебра.9 класс: учебник для общеобразоват. учреждений / Ю. Н. Макарычев, К.И.Нешков, Н. Г. Миндюк, С. Б. Суворова ; под ред. С. А. Теляковского. -М.: Просвещение, 2011.
Жохов, В. И. Дидактические материалы по алгебре.9 класс / В. И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк. - М. : Просвещение, 2011.
Обоснование выбора УМК для реализации рабочей учебной программы.
В 7-9 классах преподавание веду по УМК Макарычева Ю.Н. 7-9 кл. Под ред. Теляковского С.А. Авторы - Макарычев Ю.Н.,Миндюк Н.Г., Нешков К.И., Суворова С.В. На учебник получены положительные заключения Российской академии наук (№10106-5215/15 от 31.10.07) и Российской академии образования (№01-200/5/7д от 11.10.07)
Учебник доработан с учетом нового стандарта по математике. Темы «Степень с рациональным показателем» и «Тригонометрические выражения и их преобразования» перенесены в старшую школу. Добавлена глава «Элементы комбинаторики и теории вероятностей». Расширены темы «Уравнения и неравенства с одной переменной» и «Уравнения и неравенства с двумя переменными». Каждая глава учебника завершается дополнительным пунктом под рубрикой «Для тех, кто хочет знать больше». Учебник содержит теоретический материал, написанный доступно, на высоком научном уровне, а также систему упражнений, органически связанную с теорией. Большое внимание уделено упражнениям, которые обеспечивают усвоение основных теоретических знаний и формирование необходимых умений и навыков. Учебник 9 класса ориентирован на решение задач предпрофильного обучения. Усилена прикладная направленность курса, обновлена тематика текстовых задач. Существенно увеличено число заданий развивающего характера.
Выявление итоговых результатов изучения темы завершается контрольной работой. Контрольные работы составляются с учетом обязательных результатов обучения.
Формы и методы, технологии обучения.
Ведущими методами обучения являются: объяснительный и репродуктивный методы, частично-поисковый, метод математического моделирования, аксиоматический метод. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, дифференцированного обучения, ИКТ. Используются такие формы организации деятельности, как фронтальный опрос, групповая, парная и самостоятельная работа, работа с учебником, таблицами и др. учебными пособиями. Применяются математические диктанты, работа с дидактическими материалами и рабочими тетрадями.
Используемые формы, способы и средства проверки и оценки результатов обучения.
Письменный контроль (самостоятельные и контрольные работы, проверка домашнего задания);
Тестовый (тестирование);
Устный опрос (собеседование, зачет)
Учебно-тематический план
|
№ темы |
Название темы | Количество часов |
| теория факт. / по прог. | контрольные работы |
| 1. | Квадратичная функция | 22/22 | 2 |
| 2. | Уравнения и неравенства с одной переменной. | 14/14 | 1 |
| 3. | Уравнения и неравенства с двумя переменными. | 17/17 | 1 |
| 4. | Арифметическая и геометрическая прогрессии. | 15/15 | 2 |
| 5. | Элементы комбинаторики и теории вероятностей. | 13/13 | 1 |
| 6. | Повторение. | 21/21 | 1 |
| Всего: | 102/102 | 8/8 |
СОДЕРЖАНИЕ ОБУЧЕНИЯ
1. Свойства функций. Квадратичная функция
Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = ах2 + bх + с, её свойства и график. Степенная функция.
Основная цель: расширить сведения о свойствах функций, ознакомить обучающихся со свойствами и графиком квадратичной функции.
В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, график. Даются понятия о возрастании и убывании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.
Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квадратного трехчлена, разложении квадратного трехчлена на множители.
Изучение квадратичной функции начинается с рассмотрения функции у=ах2, её свойств и особенностей графика, а также других частных видов квадратичной функции – функции у=ах2+n, у=а(х-m)2. Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции у = ах2 + bх + с может быть получен из графика функции у = ах2 с помощью двух параллельных переносов. Приёмы построения графика функции у = ах2 + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.
При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.
Обучающиеся знакомятся со свойствами степенной функции у=хn при четном и нечетном натуральном показателе n.. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида 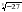 ,
, 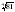 . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
2. Уравнения и неравенства с одной переменной
Целые уравнения. Дробно-рациональные уравнения. Неравенства второй степени с одной переменной. Метод интервалов.
Основная цель: систематизировать и обобщить сведения о решении целых и дробно-рациональных уравнений с одной переменной, сформирование умение решать неравенства вида ах2 + bх + с0 ах2 + bх + с где а 0.
0.
В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия целого рационального уравнения и его степени. Обучающиеся знакомятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспомогательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться дальнейшем при решении тригонометрических, логарифмических и других видов уравнений.
Расширяются сведения о решении дробных рациональных уравнений. Обучающиеся знакомятся с некоторыми специальными приемами решения таких уравнений.
Формирование умений решать неравенства вида ах2 + bх + с0 ах2 + bх + с где а 0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей параболы ее расположение относительно оси Ох).
0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей параболы ее расположение относительно оси Ох).
Обучающиеся знакомятся с методом интервалов, с помощью которого решаются несложные рациональные неравенства.
3.Уравнения и неравенства с двумя переменными
Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.
Основная цель: выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем; выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем.
В данной теме завершаемся изучение систем уравнений с двумя. переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный обучающимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения.
Ознакомление обучающихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограничиваться простейшими примерами.
Привлечение известных обучающимся графиков позволяет привести примеры графического решения систем уравнений. С помощью графических представлений можно наглядно показать обучающимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений.
Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений.
Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений.
Изучение темы завершается введением понятий неравенства с двумя переменными и системы неравенств с двумя переменными. Сведения о графиках уравнений с двумя переменными используются при иллюстрации множеств решений некоторых простейших неравенств с двумя переменными и их свойства.
4. Прогрессии
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.
Основная цель: дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий.
Работа с формулами n-го члена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.
Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.
5. Элементы комбинаторики и теории вероятностей
Комбинаторное правило умножения. Перестановки, размещения, сочетания. Относительная частота и вероятность случайного события.
Основная цель: ознакомить обучающихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.
Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и. подсчитать их число. Разъясняется комбинаторное правило умножения, которое исполнятся в дальнейшем при выводе формул для подсчёта числа перестановок, размещений и сочетаний.
При изучении данного материала необходимо обратить внимание обучающихся на различие понятий «размещение» и «сочетание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче.
В данной теме обучающиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание обучающихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными.
6. Повторение
Основная цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры основной общеобразовательной школы.
В результате изучения курса алгебры 9 класса обучающиеся должны:
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Арифметика
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций (у=кх, где к 0, у=кх+b, у=х2, у=х3, у =
0, у=кх+b, у=х2, у=х3, у =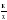 , у=
, у=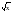 , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;
, у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
Предметная линия по геометрии для 9-го класса (2014-2015уч. года)
Рабочая программа предметной линии по геометрии для 9 класса разработана на основе Примерной программы основного общего образования с учетом требований федерального компонента государственного стандарта общего образования и с учетом программ для общеобразовательных школ, гимназий, лицеев (Геометрия. Программы общеобразовательных учреждений. 7–9 классы / сост. Т. А. Бурмистрова. М. : Просвещение, 2010).
Рабочая программа рассчитана на 68 часов. Контрольных работ – 5.
Используемый учебно-методический комплект:
Геометрия. 7–9 классы : учеб. для общеобразоват. учреждений / Л. С. Атанасян [и др]. – М.: Просвещение, 2012.
Геометрия. 9 класс. Рабочая тетрадь: пособие для учащихся общеобразовательных учреждений / Л.С. Атанасян [и др.]. – М. : Просвещение, 2011.
Зив, Б. Г. Геометрия: дидактические материалы : 9 кл. / Б. Г. Зив. – М. : Просвещение, 2011.
Изучение геометрии в 7–9 классах : метод. рекомендации : кн. для учителя / Л. С. Атанасян [и др.]. – М.: Просвещение, 2011.
Внесены элементы дополнительного содержания:
при повторении темы «Треугольники»: формулы, выражающие площадь треугольника через периметр и радиус вписанной окружности, через стороны треугольника и радиус описанной окружности, формула Герона;
при повторении темы «Четырехугольники»: площадь четырехугольника;
при изучении раздела «Правильные многоугольники»: правильные многогранники.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
| № п/п | Название раздела | Количество часов |
| Теория факт./по прог. | Контрольные работы |
-
| Вводное повторение | 2/- | - |
-
| Векторы | 8/8 | - |
-
| Метод координат | 10/10 | 1 |
-
| Соотношение между сторонами и углами треугольника | 12/12 | 1 |
-
| Длина окружности и площадь круга | 11/11 | 1 |
-
| Движение | 8/8 | 1 |
-
| Начальные сведения из стереометрии | 7/8 | - |
-
| Об аксиомах планиметрии | 2/2 | - |
-
| Повторение. | 8/9 | 1 |
| Всего: | 68/68 | 5/5 |
Принятые сокращения в тематическом планировании
| Тип урока | Форма контроля |
| УОНМ – урок ознакомления с новым материалом | К/Р – контрольная работа |
| УЗИМ – урок закрепления изученного материала |
|
| УПЗУ – урок применения знаний и умений |
|
| КУ – комбинированный урок |
|
| КЗУ – контроль знаний и умений |
|
| УОСЗ – урок обобщения и систематизации знаний |
|
СОДЕРЖАНИЕ ОБУЧЕНИЯ
1. Векторы. Метод координат
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.
Основная цель - научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач.
Вектор определяется как направленный отрезок и действия над векторами вводятся так, как это принято в физике, т. е. как действия с направленными отрезками. Основное внимание должно быть уделено выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и параллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число).
На примерах показывается, как векторы могут применяться к решению геометрических задач. Демонстрируется эффективность применения формул для координат середины отрезка, расстояния между двумя точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым дается представление об изучении геометрических фигур с помощью методов алгебры.
2. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов.
Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах.
Основная цель - развить умение учащихся применять тригонометрический аппарат при решении геометрических задач.
Синус и косинус любого угла от 0° до 180° вводятся с помощью единичной полуокружности, доказываются теоремы синусов и косинусов и выводится еще одна формула площади треугольника (половина произведения двух сторон на синус угла между ними). Этот аппарат применяется к решению треугольников.
Скалярное произведение векторов вводится как в физике (произведение длин векторов на косинус угла между ними). Рассматриваются свойства скалярного произведения и его применение при решении геометрических задач.
Основное внимание следует уделить выработке прочных навыков в применении тригонометрического аппарата при решении геометрических задач.
3. Длина окружности и площадь круга
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
Основная цель - расширить знание учащихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления.
В начале темы дается определение правильного многоугольника и рассматриваются теоремы об окружностях, описанной около правильного многоугольника и вписанной в него. С помощью описанной окружности решаются задачи о построении правильного шестиугольника и правильного 2 n -угольника, если дан правильный n-угольник.
Формулы, выражающие сторону правильного многоугольника и радиус вписанной в него окружности через радиус описанной окружности, используются при выводе формул длины окружности и площади круга. Вывод опирается на интуитивное представление о пределе: при неограниченном увеличении числа сторон правильного многоугольника, вписанного в окружность, его периметр стремится к длине этой окружности, а площадь - к площади круга, ограниченного окружностью.
4. Движения
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения.
Основная цель - познакомить учащихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений.
Движение плоскости вводится как отображение плоскости на себя, сохраняющее расстояние между точками. При рассмотрении видов движений основное внимание уделяется построению образов точек, прямых, отрезков, треугольников при осевой и центральной симметриях, параллельном переносе, повороте. На эффектных примерах показывается применение движений при решении геометрических задач.
Понятие наложения относится в данном курсе к числу основных понятий. Доказывается, что понятия наложения и движения являются эквивалентными: любое наложение является движением плоскости и обратно. Изучение доказательства не является обязательным, однако следует рассмотреть связь понятий наложения и движения.
5. Об аксиомах геометрии
Беседа об аксиомах по геометрии.
Основная цель - дать более глубокое представление о системе аксиом планиметрии и аксиоматическом методе.
В данной теме рассказывается о различных системах аксиом геометрии, в частности о различных способах введения понятия равенства фигур.
6. Начальные сведения из стереометрии
Предмет стереометрии. Геометрические тела и поверхности. Многогранники: призма, параллелепипед, пирамида, формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их площадей поверхностей и объемов.
Основная цель - дать начальное представление о телах и поверхностях в пространстве; познакомить учащихся с основными формулами для вычисления площадей поверхностей и объемов тел.
Рассмотрение простейших многогранников (призмы, параллелепипеда, пирамиды), а также тел и поверхностей вращения (цилиндра, конуса, сферы, шара) проводится на основе наглядных представлений, без привлечения аксиом стереометрии. Формулы для вычисления объемов указанных тел выводятся на основе принципа Кавальери, формулы для вычисления площадей боковых поверхностей цилиндра и конуса получаются с помощью разверток этих поверхностей, формула площади сферы приводится без обоснования.
7. Повторение. Решение задач
В результате изучения курса геометрии 9 класса обучающиеся должны:
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Геометрия
уметь
пользоваться языком геометрии для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения геометрических задач с использованием тригонометрии
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Способы достижения и формы оценки результатов обучения:
Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.
Оценка устных ответов учащихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания
Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.
допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).
имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменных контрольных работ учащихся.
Отметка «5» ставится в следующих случаях:
работа выполнена полностью.
в логических рассуждениях и обоснованиях нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала)
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков
Поурочное планирование
| Номер урока | Тема
урока | К-во часов | Тип
урока | Элементы содержания | Требования
к уровню подготовки учащихся | Элементы
дополни-
тельного
содержания | Дата проведения |
| план | факт |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Квадратичная функция (22 часа) |
| 1–2 | Функция. Область определения и область значений функции. | 2 | Актуализация знаний и умений | Функция. Область определения, множество значений функции. Примеры функциональных зависимостей. Возрастание и убывание функции | Знать понятие функции и другую функциональную терминологию. Уметь правильно употреблять функциональную терминологию, понимая ее в тексте, в речи учителя, в формулировке задач; находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу | Умение свободно читать графики, описывать свойства функции по графику |
|
|
| 3 | Функция. Область определения и область значений функции. | 1 | Ознакомление с новым учебным материалом | Графики функций, содержащих переменную под знаком модуля |
|
|
| 4–5 | Свойства функций | 2 | Закрепление изученного
материала |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 6 | Квадратный трехчлен
Применение теоремы о разложении квадратного трехчлена на множители для преобразования выражений. | 1 | Ознакомление с новым учебным материалом | Квадратный трехчлен Корни квадратного трехчлена. Выделение квадрата двучлена из квадратного трехчлена. Разложение квадратного трехчлена
на множители | Знать понятие квадратного трехчлена, формулу
разложения квадратного трехчлена на множители. Уметь выделять квадрат двучлена из квадратного трехчлена, раскладывать трехчлен на множители | Умение самостоятельно выбрать рациональный способ разложения квадратного трехчлена на множители |
|
|
| 7 | 1 | Закрепление изученного материала |
|
|
| 8 | 1 | Применение знаний
и умений |
|
|
| 9 | 1 | Применение знаний
и умений |
|
|
| 10 | Входная контрольная работа | 1 | Контроль знаний и умений | Функция. Область определения, множество значений функции. Квадратный трехчлен. Корни квадратного трехчлена. Разложение квадратного трехчлена на множители | Уметь находить корни квадратного трехчлена и раскладывать его на множители |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 11 | Анализ к\р Функция у = ах2,
ее график
и свойства | 1 | Комбинированный урок | Функция у = ах2 , график функции | Знать и понимать функции
у = ах2, их свойства и особенности графиков | Умение решать графически уравнения и системы уравнений, определять число решений системы уравнений с помощью графического метода
|
|
|
| 12 | 1 | Применение знаний
и умений | Уметь строить график функции у = ах2 |
|
|
| 13 | Графики функций у = ах2 +
+ п и у =
= а (х – т)2 | 1 | Ознакомление с новым учебным материалом | Квадратичная функция. Преобразование графика функции | Знать и понимать функции у = ах2 + п и у = а (х – т)2, их свойства и особенности графиков. Уметь строить графики функций у = ах2 + п и у = а (х – т)2,
выполнять простейшие преобразования графиков | Умение
по алгоритму построить графики функций y = f (x + n), y = f (x) + m, y = f (x + n) + + m, прочитать и описать свойства |
|
|
| 14 | 1 | Применение знаний
и умений
|
|
|
|
| 15 | 1 | Систематизация знаний
|
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 16 | Построение графика квадратичной функции | 1 | Ознакомление с новым учебным материалом | Функция y = ax2 + bx + c. Промежутки возрастания и убывания квадратичной функции | Знать, что график функции y = ax2 + bx + c может быть получен из графика функции y = ax2 с помощью двух параллельных переносов вдоль осей координат. Уметь строить график квадратичной функции, находить по графику промежутки возрастания и убывания функции, промежутки знакопостоянства, наибольшее и наименьшее значения | Умение свободно применять несколько способов графического решения уравнения |
|
|
| 17 | 1 | Закрепление изученного материала |
|
|
| 18 | 1 | Обобщение и систематизация знаний |
|
|
| 19 | Степенная функция. Корень п-й степени
Обобщающий урок «Квадратичная функция и её график» | 1 | Ознакомление с новым учебным материалом | Функция у = хп. Определение корня п-й
степени | Знать свойства степенной функции с натуральным показателем, понятие корня п-й степени. Уметь перечислять свойства степенных функций, схематически строить графики функций, указывать особенности графиков, вычислять корни
п-й степени (несложных заданий) | Степень с рациональным показателем и ее свойства |
|
|
| 20 | 1 | Применение знаний
и умений |
|
|
| 21 | 1 | Систематизация знаний |
|
|
| 22 | К/р 2 «Квадратичная функция и её график» | 1 | Контроль знаний
и умений | Квадратичная функция. Преобразование графиков функций. Функции у = хп.
Определение корня п-й степени | Уметь строить график квадратичной функции, находить по графику промежутки возрастания и убывания функции, промежутки знакопостоянства, наибольшее и наименьшее значения, вычислять корни п-й степени (несложных заданий) |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Уравнения и неравенства с одной переменной (14 часов) |
| 23 | Анализ к\р Целое уравнение и его корни | 1 | Комбинированный урок | Целое уравнение и его корни. Степень уравнения | Знать понятие целого рационального уравнения и его степени, приемы нахождения приближенных значений корней. Уметь решать уравнения третьей и четвертой степени с одним неизвестным с помощью разложения на множители |
|
|
|
| 24 | 1 | Применение знаний
и умений | Уравнения
с параметрами |
|
|
| 25 | Уравнения, приводимые к квадратным | 1 | Изучение нового
материала | Целое уравнение и его корни. Степень уравнения. Биквадратное уравнение. Уравнения, приводимые к квадратным, и методы их решения
| Знать понятие целого рационального уравнения и его степени, метод введения вспомогательной переменной. Уметь решать уравнения третьей
и четвертой степени с одним неизвестным с помощью введения вспомогательной переменной |
|
|
|
| 26 |
| 1 | Закрепление изученного материала |
|
| Уравнения
с параметрами |
|
|
| 27 |
| 1 | Применение знаний
и умений |
|
|
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 28 | Дробные рациональные уравнения | 1 | Изучение нового
материала | Дробное рациональное уравнение, алгоритм их решения | Знать о дробных рациональных
уравнениях, об освобождении от знаменателя при решении уравнений. Уметь решать дробные рациональные уравнения, применяя формулы сокращенного умножения и разложения квадратного трехчлена на множители | Специальные приемы решения целых уравнений; теорема о корне многочлена; решение возвратных уравнений |
|
|
| 29 | 1 | Закрепление изученного материала |
|
|
| 30 | 1 | Проверка
и коррекция знаний |
|
|
| 31 | Решение
неравенств
второй
степени
с одной переменной | 1 | Изучение нового
материала | Решение неравенств второй степени с одной переменной | Знать понятие неравенства второй степени с одной переменной и методы их решения. Уметь решать неравенства второй степени с одной переменной, применять графическое представление для решения неравенств второй степени с одной
переменной |
|
|
|
| 32 | 1 | Закрепление изученного материала | Неравенства
с параметрами |
|
|
| 33 | Решение
неравенств
методом интервалов | 1 | Ознакомление с новым учебным материалом | Метод интервалов | Уметь применять метод интервалов при решении неравенств с одной переменной, дробных
рациональных неравенств |
|
|
|
| 34 |
| 1 | Применение знаний
и умений |
|
|
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 35 | Обобщающий урок «Целые уравнения. Неравенства второй степени с одной переменной." | 1 | Систематизация знаний |
|
|
|
|
|
| 36 | К\р 3 «Целые уравнения. Неравенства второй степени с одной переменной." | 1 | Контроль знаний
и умений | Уравнения
неравенств с одной переменной. Метод интервалов | Уметь решать уравнения и неравенства с одной переменной |
|
|
|
| Уравнения и неравенства с двумя переменными (17 часов) |
| 37 | Анализ к\р Уравнения с двумя переменными и его график | 1 | Комбинированный урок | Уравнения с двумя переменными и его график. Уравнение окружности | Знать и понимать уравнение с двумя переменными и его график. Уравнение окружности |
|
|
|
| 38 | Графический способ решения систем уравнений | 1 | Изучение нового
материала | Системы двух уравнений второй степени с двумя переменными | Знать системы двух уравнений второй степени с двумя переменными и графический способ их решения. Уметь решать графически системы уравнений |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 39 |
| 1 | Закрепление изученного материала |
|
|
|
|
|
| 40 | Решение систем уравнений второй
степени способом подстановки | 1 | Изучение нового
материала | Системы двух уравнений второй степени с двумя переменными | Знать системы двух уравнений
второй степени с двумя переменными и методы их решения. Уметь решать системы, содержащие одно уравнение первой, а другое – второй степени, системы двух уравнений второй степени с двумя переменными | Системы двух уравнений второй степени с двумя переменными с помощью различных приемов |
|
|
| 41 | 1 | Закрепление изученного материала |
|
|
| 42 | Использование способа сложения при решение систем уравнения второй степени | 1 | Изучение нового
материала |
|
|
|
| 43 | 1 | Закрепление изученного материала |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 44 | Решение
задач с помощью
систем уравнений второй степени
Решение задач на движение с помощью систем уравнений второй степени | 1 | Изучение нового
материала | Системы уравнений второй степени | Знать и понимать системы двух уравнений второй степени с двумя переменными и методы их решения. Уметь решать текстовые задачи методом составления систем уравнений | Умение свободно составлять математические модели реальных ситуаций и работать с составленной моделью |
|
|
| 45 | 1 | Закрепление изученного материала |
|
|
| 46 | 1 | Применение знаний
и умений |
|
|
| 47 | Решение задач на работу с помощью систем уравнений второй степени | 1 | Применение знаний
и умений |
|
|
|
| 48 | 1 | Обобщение и систематизация знаний |
|
|
|
| 49 | Неравенства с двумя переменными | 1 | Изучение нового
материала | Неравенства с двумя переменными; решение неравенств
с двумя переменными | Иметь представление о решении неравенств с двумя переменными. Уметь изображать на координатной плоскости множество решений неравенств |
|
|
|
| 50 | 1 | Закрепление изученного материала |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 51 | Системы неравенств
с двумя
переменными
Обобщающий урок «Системы уравнений второй степени» | 1 | Изучение нового
материала | Системы неравенств с двумя переменными.
Решение системы неравенств с двумя переменными | Иметь представление о решении системы неравенств с двумя переменными. Уметь изображать множество
решений системы неравенств с двумя переменными на координатной плоскости
|
|
|
|
| 52 | 1 | Систематизация изученного материала |
|
|
|
| 53 | К/р 4 «Системы уравнений второй степени» | 1 | Контроль знаний
и умений | Уравнения неравенства с двумя переменными
и их решения | Уметь решать системы уравнений, системы неравенств и задачи
с помощью систем уравнений с двумя переменными |
|
|
|
| Арифметическая и геометрическая прогрессии (15 часов) |
| 54 | Анализ к\р Последовательности | 1 | Комбинированный урок | Последовательности | Знать понятия последовательности, п-го члена последовательности. Уметь использовать индексные обозначения |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 55 | Определение арифметической прогрессии. Формула
п-го члена арифметической прогрессии | 1 | Изучение нового
материала | Последовательность п-го члена последовательности. | Знать определение: арифметическая прогрессия – числовая после- довательность особого вида. Уметь решать упражнения и задачи, в том числе практического содержания, с непосредственным применением изучаемых формул |
|
|
|
| 56 | 1 | Применение знаний
и умений | Арифметическая прогрессия. Формула п-го члена арифметической прогрессии. Характеристическое свойство арифметической прогрессии |
|
|
|
| 57 | 1 | Обобщение и систематизация знаний |
|
|
|
| 58 | Формула суммы п первых членов арифметической прогрессии
Обобщающий урок «Арифметическая прогрессия» | 1 | Изучение нового
материала | Арифметическая прогрессия. Формула п-го члена арифметической прогрессии. Формула суммы п первых членов арифметической прогрессии | Знать и понимать формулы п-первых членов арифметической прогрессии. Уметь решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул |
|
|
|
| 59 | 1 | Применение знаний
и умений |
|
|
|
| 60 | 1 | Обобщение и систематизация знаний
|
|
|
|
| 61 | К/р 5 «Арифметическая прогрессия» | 1 | Проверка знаний | Арифметическая прогрессия. Формула п-го члена арифметической прогрессии. Формула суммы п первых членов арифметической прогрессии | Уметь решать задания на применение свойств арифметической прогрессии |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 62 | Анализ к\р Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии | 1 | Изучение нового материала | Последовательность, формула п-го члена последовательности. Геометрическая прогрессия. Формула п-го члена геометрической прогрессии. Характеристическое свойство геометрической прогрессии | Знать и понимать: геометрическая прогрессия – числовая последовательность особого вида. Уметь решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул |
|
|
|
| 63 | 1 | Закрепление изученного материала |
|
|
|
| 64 | 1 | Применение знаний
и умений |
|
|
|
| 65 | Формула суммы п первых членов геометрической прогрессии
Обобщающий урок «Геометрическая прогрессия» | 1 | Изучение нового
материала
| Геометрическая прогрессия. Формула п-го члена геометрической прогрессии. Формула суммы п первых членов геометрической прогрессии | Знать и понимать формулы
п первых членов геометрической прогрессии. Уметь решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул | Бесконечно убывающая
геометрическая прогрессия и сумма
ее членов |
|
|
| 66 |
| 1 | Применение знаний
и умений
|
|
|
|
|
|
| 67 |
| 1 | Систематизация и обобщение материала
|
|
|
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 68 | К/р 6 «Геометрическая прогрессия» | 1 | Контроль знаний
и умений | Геометрическая прогрессия. Формула п-го члена геометрической прогрессии. Формула суммы п первых членов геометрической прогрессии | Уметь применять формулы п-го члена и суммы п первых членов геометрической прогрессии при решении задач |
|
|
|
| Элементы комбинаторики и теории вероятностей (13 часов) |
| 69 | Анализ к\р Элементы комбинаторики. Примеры комбинаторных задач | 1 | Изучение нового
материала | Примеры комбинаторных задач | Знать и понимать комбинаторное правило умножения, формулы числа перестановок, размещений, сочетаний |
|
|
|
| 70 |
| 1 | Закрепление изученного материала |
|
|
|
|
|
| 71 | Перестановки | 1 | Изучение нового
материала | Перестановки | Уметь решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул |
|
|
|
| 72 |
| 1 | Закрепление полученных
знаний |
|
|
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 73 | Размещения | 1 | Изучение нового
материала | Размещения | Уметь решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул |
|
|
|
| 74 | 1 | Закрепление изученного материала |
|
|
|
| 75 | Сочетания | 1 | Изучение нового
материала | Сочетания | Уметь решать упражнения и задачи, в том числе практического содержания с непосредственным применением изучаемых формул |
|
|
|
| 76 | 1 | Применение знаний
и умений |
|
|
|
| 77 | 1 | Обобщение и систематизация знаний |
|
|
|
| 78 | Начальные сведения из теории вероятностей. Относительная частота
случайного события. Вероятность равновозможных
событий | 1 | Изучение нового
материала | Случайные,
достоверные,
невозможные события. Статистическое и классическое определение
вероятности | Знать и понимать теории
вероятностей. Уметь: – вычислять
вероятности; – использовать
формулы комбинаторики |
|
|
|
| 79 |
| 1 | Закрепление полученных
знаний |
|
| Сложение
и умножение вероятностей
(пункт 36) |
|
|
| 80 |
| 1 | Проверка
и коррекция знаний
и умений |
|
|
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 81 | К/р 7 "Элементы комбинаторики и теории вероятностей" | 1 | Проверка знаний
и умений | Перестановки, размещения, сочетания, вероятность равновозможных событий | Уметь решать задачи, используя формулы комбинаторики и теории
вероятностей |
|
|
|
| Повторение (21 час) |
| 82 | Анализ к\р. Повторение. Вычисления | 1 | Комбинированный урок | Числовые выражения. Арифметический квадратный корень. Арифметическая и геометрическая прогрессии. Степень с натуральным и отрицательным показателями | Уметь находить значения числовых и буквенных выражений; применять формулы п-го члена и суммы арифметической и геометрической прогрессии |
|
|
|
| 83 | 1 | Комбинированный урок |
|
|
|
| 84 | Повторение. Тождественные преобразования | 1 | Обобщение и систематизация знаний | Действия с многочленами, дробными рациональными выражениями и выражениями, содержащими квадратные корни. Формулы сокращенного умножения | Уметь: – выполнять действия с многочленами, дробными рациональными
выражениями; – применять формулы сокращенного умножения; – упрощать выражения, содержащие квадратные корни; – раскладывать многочлен на множители различными способами |
|
|
|
| 85 |
| 1 | Комбинированный урок |
|
|
|
|
|
| 86 |
| 1 | Комбинированный урок |
|
|
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 87 | Повторение. Уравнения
и системы уравнений
Решение текстовых задач на составление уравнений и систем уравнений.
| 1 | Обобщение и систематизация знаний | Уравнения с одной переменной и системы уравнений с двумя переменными. Арифметическая и геометрическая прогрессии | Уметь решать уравнения с одной переменной и системы уравнений
с двумя переменными; задачи
с помощью составления уравнения или системы уравнений с двумя переменными |
|
|
|
| 88 | 1 | Комбинированный урок |
|
|
|
| 89 | 1 | Комбинированный урок |
|
|
|
| 90 | 1 | Комбинированный урок |
|
|
|
| 91 | 1 | Комбинированный урок |
|
|
|
| 92 | 1 | Комбинированный урок |
|
|
|
| 93 | Повторение. Неравенства | 1 | Обобщение и систематизация знаний | Неравенства
и системы неравенств с одной переменной. Область определения выражения | Уметь решать неравенства и системы неравенств с одной переменной |
|
|
|
| 94 |
| 1 | Комбинированный урок |
|
|
|
|
|
| 95 |
| 1 | Комбинированный урок |
|
|
|
|
|
Окончание табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 96 | Повторение. Функции | 1 | Обобщение и систематизация знаний | Функция. График функции. Свойства функции | Уметь: – строить графики функций; – исследовать функцию на монотонность; – находить промежутки знакопостоянства; – область определения и область значений функции |
|
|
|
| 97 | 1 | Комбинированный урок |
|
|
|
| 98 | 1 | Комбинированный урок |
|
|
|
|
| 99–
100 | Итоговая контрольная работа | 2 | Контроль знаний
и умений |
| Уметь решать задания по изученному материалу |
|
|
|
| 101 | Анализ контрольной работы | 1 | Обобщение и систематизация знаний |
| Уметь решать задания по изученному материалу |
|
|
|
| 102 | Подведение итогов | 1 |
|
|
|
|
Методические пособия для учителя:
Программа для общеобразовательных учреждений. Математика. Министерство образования Российской Федерации.
Федеральный общеобразовательный стандарт. Вестник образования. №12,2004.
Макарычев Ю.Н. Алгебра 9. Учебник для учащихся 9 класса. – М., Мнемозина, 2010г.
Макарычев Ю.Н., Н.Г. Миндюк, Л.М. Короткова «Дидактические материалы по алгебре для 9 класса М., Просвещение 1996г
Алтынов П.И. Тесты. Алгебра (7-9 кл.). М.:Дрофа 2000г
CD «Уроки геометрии Кирилла и Мефодия 7-9 классы»
В.И. Жохов, Г.Д. Карташева, Л.Б. Крайнева – «Уроки геометрии в 7-9 классах», методические рекомендации для учителя к учебнику Л.С. Атанасяна, 2003г.
Б.Г. Зив. Дидактические материалы по геометрии для 9 класса- М. Просвещение, 2003.
Л. С. Атанасян, В. Ф. Бутузов. Ю. А. Глазков, В. Б. Некрасов, И. И. Юдина Изучение геометрии в 7-9 классах. Методические рекомендации.- М.: Просвещение 2003 г.
Образовательные диски.
поурочное планирование
| № п/п | Тема урока | Кол-во часов | Тип
урока | Элементы содержания | Требования к уровню подготовки обучающихся | Элементы дополнительного содержания | Дата проведения |
| план. | факт. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Вводное повторение (2 ч) |
| 1 | Повторение. Треугольники | 1 | Обобщение и систематизация знаний | 1) Классификация треугольников по углам, сторонам. 2) Элементы треугольника. 3) Признаки равенства треугольников. 4) Прямоугольный треугольник. 5) Теорема Пифагора | Знать: классификацию треугольников по углам и сторонам; формулировку трех признаков равенства треугольников; свойства равнобедренного и прямоугольного треугольника. Уметь: применять вышеперечисленные факты при решении геометрических задач; находить стороны прямоугольного треугольника по теореме Пифагора |
|
|
|
| 2 | Повторение. Четырехугольники | 1 | Обобщение и систематизация знаний | 1) Параллелограмм, его свойства и признаки. 2) Виды параллелограммов и их свойства и признаки. 3) Трапеция, виды трапеций | Знать: классификацию параллелограммов; определения параллелограмма, ромба, прямоугольника, квадрата, трапеции. Уметь: формулировать их свойства и признаки; применять определения, свойства и признаки при решении задач; изображать чертеж по условию задачи
|
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Векторы (8 ч) |
| 3 | Понятие вектора, равенство векторов | 1 | УОНМ | 1) Вектор. 2) Длина вектора. 3) Равенство векторов. 4) Коллинеарные векторы | Знать: определение вектора и равных векторов. Уметь: обозначать и изображать векторы, изображать вектор, равный данному |
|
|
|
| 4 | Сумма двух векторов.
Законы
сложения | 1 | УОНМ | 1) Сложение векторов. 2) Законы сложения. 3) Правило
треугольника. 4) Правило параллелограмма | Знать: законы сложения, определение суммы, правило треугольника, правило параллелограмма. Уметь: строить вектор, равный сумме двух векторов, используя правила треугольника, параллелограмма, формулировать законы сложения |
|
|
|
| 5 | Сумма нескольких векторов | 1 | КУ | Правило
многоугольника | Знать: понятие суммы двух и более векторов. Уметь: строить сумму нескольких векторов, используя правило многоугольника |
|
|
|
| 6 | Вычитание векторов | 1 | КУ | 1) Разность двух векторов. 2) Противоположный вектор | Знать: понятие разности двух векторов, противоположного вектора. Уметь: строить вектор, равный разности двух векторов, двумя способами |
|
|
|
| 7 | Умножение вектора на число | 1 | УОНМ | 1) Умножение вектора на число. 2) Свойства умножения | Знать: определение умножения вектора на число, свойства. Уметь: формулировать свойства, строить вектор, равный произведению вектора на число, используя опред-ние |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 8 | Умножение вектора на число | 1 | УКЗУ | Свойства умножения вектора на число | Уметь: решать задачи на применение свойств умножения вектора на число |
|
|
|
| 9 | Применение векторов к решению задач | 1 | УПЗУ | Задачи на применение векторов | Уметь: решать геометрические задачи на алгоритм выражения вектора через данные векторы, используя правила сложения, вычитания и умножения вектора на число |
|
|
|
| 10 | Средняя
линия
трапеции | 1 | УОНМ | 1) Понятие средней линии трапеции. 2) Теорема о средней линии трапеции | Знать: определение средней линии трапеции. Понимать: суть теоремы о средней линии трапеции и алгоритм решения задач с применением этой теоремы |
|
|
|
| Метод координат (10 ч) |
| 11 | Разложение вектора по двум неколлинеарным векторам | 1 | УОНМ | 1) Координаты вектора; длина вектора. 2) Теорема о разложении вектора по двум неколлинеарным векторам | Знать и понимать: суть леммы о коллинеарных векторах и теоремы о разложении вектора по двум неколлинеарным векторам. Уметь: проводить операции над векторами с заданными координатами |
|
|
|
| 12 | Координаты вектора | 1 | УОНМ | Координаты вектора, правила действия над векторами с заданными координатами | Знать: понятия координат вектора, координат суммы и разности векторов, произведения вектора на число |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 13 | Координаты вектора | 1 | УПЗУ | Действия над векторами | Знать: определение суммы, разности векторов, произведения вектора на число. Уметь: решать простейшие задачи методом координат |
|
|
|
| 14 | Простейшие задачи в координатах | 1 | УОНМ | Координаты вектора, координаты середины отрезка, длина вектора, расстояние между двумя точками | Знать: формулы координат вектора через координаты его конца и начала, координат середины отрезка, длины вектора и расстояния между двумя точками. Уметь: решать геометрические задачи с применением этих формул |
|
|
|
| 15 | 1 | КУ |
|
|
|
| 16 | Уравнение линии на плоскости. Уравнение окружности | 1 | УОНМ | Уравнение окружности | Знать: уравнения окружности. Уметь: решать задачи на определение координат центра окружности и его радиуса по заданному уравнению окружности. Уметь: составлять уравнение окружности, зная координаты центра и точки окружности |
|
|
|
| 17 | Уравнение прямой | 1 | КУ | Уравнение
прямой | Знать: уравнение прямой. Уметь: составлять уравнение прямой по координатам двух ее точек |
|
|
|
| 18 | Уравнения окружности и прямой | 1 | УОСЗ | Уравнения окружности и прямой | Знать: уравнения окружности и прямой. Уметь: изображать окружности и прямые, заданные уравнениями, решать простейшие задачи в координатах |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 19 | Решение
задач | 1 | УЗИМ | Задачи по теме «Метод
координат» | Знать: правила действий над векторами с заданными координатами(суммы, разности, произведения вектора на число); формулы координат вектора через координаты его начала и конца, координаты середины отрезка; формулу длины вектора по его координатам; формулу нахождения расстояния между двумя точками через их координаты; уравнения окружности и прямой. Уметь: решать простейшие геометрические задачи, пользуясь указанными формулами |
|
|
|
| 20 | К/р 1 . «Метод координат» | 1 | УПЗУ | Контроль и оценка знаний и умений | Уметь: решать простейшие задачи методом координат, вычислять длину и координаты вектора, угол между векторами |
|
|
|
| Соотношение между сторонами и углами треугольника (12 ч) |
| 21 | Анализ к/р. Синус, косинус и тангенс угла | 1 | УОНМ | 1) Синус, косинус, тангенс. 2) Основное тригонометрическое
тождество. 3) Формулы приведения. 4) Синус, косинус, тангенс углов от 0º
до 180º | Знать: определения синуса, косинуса и тангенса углов от 0º до 180º, формулы для вычисления координат точки, основное тригонометрическое тождество. Уметь: применять тождество при решении задач на нахождение одной тригонометрической функции через другую |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 22 | Синус, косинус и тангенс угла | 1 | КУ | Формулы для вычисления координат точки | Знать: формулу основного тригонометрического тождества, простейшие формулы приведения. Уметь: определять значения тригонометрических функций для углов от 0º до 180º по заданным значениям углов; находить значения тригонометрических функций по значению одной из них |
|
|
|
| 23 | Теорема
о площади треугольника | 1 | УОНМ | Формулы,
выражающие площадь треугольника через две стороны и угол между ними | Знать: формулу площади треугольника: 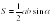 . . Уметь: реализовывать этапы доказательства теоремы о площади треугольника, решать задачина вычисление площади треугольника | Формула Герона |
|
|
| 24 | Теорема
синусов | 1 | УОНМ | 1) Теорема синусов. 2) Примеры применения теоремы для вычисления элементов треугольника | Знать: формулировку
теоремы синусов Уметь: проводить доказательство теоремы и применять ее при решении задач |
|
|
|
| 25 | Теорема косинусов | 1 | КУ | 1) Теорема
косинусов. 2) Примеры применения | Знать: формулировку теоремы косинусов. Уметь: проводить доказательство теоремы и применять ее для нахождения элементов треугольника |
|
|
|
| 26 | Соотношение между сторонами и углами треугольника | 1 | УПЗУ | Задачи на использование теорем синусов
и косинусов | Знать: основные виды задач. Уметь: применять теоремы синусов и косинусов, выполнять чертеж по условию задачи |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 27 | Соотношение между сторонами и углами
треугольника | 1 | УПЗУ | Решение треугольников | Знать: способы решения треугольников. Уметь: решать треугольники по двум сторонам и углу между ними; по стороне и прилежащим к ней углам; по трем сторонам |
|
|
|
| 28 | Решение треугольников. Измерительные работы | 1 | КУ | Методы решения задач, связанные с измерительными
работами | Знать: методы проведения измерительных работ. Уметь: выполнять чертеж по условию задачи, применять теоремы синусов и косинусов при выполнении измерительных работ на местности |
|
|
|
| 29 | Угол между векторами. Скалярное произведение векторов | 1 | УОНМ | Понятие угла между векторами, скалярного произведения векторов и его свойств, скалярный квадрат
вектора | Знать: что такое угол между векторами, определение скалярного произведения векторов, условие перпендикулярности ненулевых векторов. Уметь: изображать угол между векторами, вычислять скалярное
произведение |
|
|
|
| 30 | Скалярное произведение векторов в координатах | 1 | КУ | Понятие скалярного произведения
векторов в координатах и его свойства | Знать: теорему о скалярном произведении двух векторов и ее
следствия. Уметь: доказывать теорему, находить углы между векторами, используя формулу скалярного произведения в координатах |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 31 | Решение
треугольников. Скалярное произведение векторов | 1 | УПЗУ | Задачи на применение теорем синусов
и косинусов
и скалярного произведения векторов | Знать: формулировки теоремы синусов, теоремы косинусов, теоремы о нахождении площади треугольника, определение скалярного произведения и формулу в координатах. Уметь: решать простейшие планиметрические задачи |
|
|
|
| 32 | К/Р 2. «Соотношение между сторонами и углами треугольника» | 1 | УКЗУ | Контроль и оценка знаний по теме | Уметь: решать геометрические задачи с использованием тригонометрии |
|
|
|
| Длина окружности и площадь круга (11 ч) |
| 33 | Анализ к/р. Правильные многоугольники | 1 | КУ | 1) Понятие правильного многоугольника. 2) Формула для вычисления угла правильного
n-угольника | Знать: определение правильного многоугольника, формулу для вычисления угла правильного n-угольника. Уметь: выводить формулу для вычисления угла правильного n-угольника и применять ее в процессе решения задач |
|
|
|
| 34 | Окружность, описанная около правильного многоугольника
и вписанная в правильный многоугольник | 1 | УОНМ | Теоремы об окружности, описанной около правильного многоугольника, и окружности, вписанной в него | Знать: формулировки теорем и следствия из них. Уметь: проводить доказательства теорем и следствий из теорем и применять их при решении задач |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 35 | Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности | 1 | УОНМ | Формулы, связывающие площадь и сторону правильного многоугольника
с радиусами вписанной и описанной окружностей | Знать: формулы площади, стороны правильного многоугольника, радиуса вписанной окружности. Уметь: применять формулы при решении задач |
|
|
|
| 36 | Правильные многоугольники | 1 | УПЗУ | Задачи на построение правильных многоугольников | Уметь: строить правильные многоугольники с помощью циркуля и линейки | Правильные многогранники |
|
|
| 37 | Правильные многоугольники | 1 | УОСЗ | Задачи по теме «Правильные многоугольники» | Уметь: решать задачи на применение формулы для вычисления площади, стороны правильного многоугольника и радиуса вписанной окружности |
|
|
|
| 38 | Длина окружности | 1 | УОНМ | 1) Формула длины окружности. 2) Формула длины дуги окружности | Знать: формулы длины окружности и ее дуги. Уметь: применять формулы при решении задач |
|
|
|
| 39 | Длина окружности. Решение задач | 1 | УПЗУ | Задачи на применение формул длины окружности и длины дуги окружности | Знать: формулы. Уметь: выводить формулы длины окружности и длины дуги окружности, применять формулы для решения задач |
|
|
|
| 40 | Площадь круга
и кругового сектора | 1 | УОНМ | Формулы площади круга и кругового
сектора | Знать: формулы площади круга и кругового сектора, иметь представление о выводе формулы. Уметь: находить площадь круга и кругового сектора |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 41 | Площадь круга. Решение задач | 1 | УПЗУ | Задачи на применение формул площади круга и кругового сектора | Знать: формулы. Уметь: решать задачи
с применением формул |
|
|
|
| 42 | Решение задач «Длина окружности. Площадь круга» | 1 | УОСЗ | 1) Длина окружности. 2) Площадь круга | Использовать: приобретенные знания и умения в практической деятельности |
|
|
|
| 43 | К/Р 3 «Длина окружности. Площадь круга» | 1 | УКЗУ | Контроль и оценка знаний и умений | Знать: формулы длины окружности, дуги окружности, площади круга и кругового сектора. Уметь: решать простейшие задачи с использованием этих формул |
|
|
|
| Движение (8 ч) |
| 44 | Анализ к/р. Понятие
движения | 1 | КУ | Понятие отображения плоскости на себя и движение | Знать: понятие отображения плоскости на себя и движения. Уметь: выполнять построение движений, осуществлять преобра-
зования фигур |
|
|
|
| 45 | Понятие
движения | 1 | УОНМ | Осевая и центральная симметрия | Знать: осевую и центральную симметрию. Уметь: распознавать по чертежам, осуществлять преобразования фигур с помощью осевой и центральной симметрии |
|
|
|
| 46 | Понятие
движения | 1 | КУ | Свойства
движения | Знать: свойства движения. Уметь: применять свойства движения при решении задач |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 47 | Параллельный перенос | 1 | УОНМ | Движение фигур с помощью параллельного переноса | Знать: основные этапы доказательства, правило: параллельный перенос есть движение. Уметь: применять параллельный перенос при решении задач |
|
|
|
| 48 | Поворот | 1 | УОНМ | Поворот | Знать: определение поворота. Уметь: доказывать, что поворот есть движение, осуществлять поворот фигур |
|
|
|
| 49 | Решение задач по теме «Параллельный перенос. Поворот» | 1 | УПЗУ | Движение фигур с помощью параллельного переноса и поворота | Знать: определение параллельного переноса и поворота. Уметь: осуществлять параллельный перенос и поворот фигур |
|
|
|
| 50 | Решение задач по теме «Движение» | 1 | УОСЗ | Задачи с применением
движения | Знать: все виды движений. Уметь: выполнять построение движений с помощью циркуля
и линейки |
|
|
|
| 51 | К/Р 4 «Движение» | 1 | УКЗУ | Контроль
и оценка знаний и умений |
|
|
|
|
| Начальные сведения из стереометрии (7 ч) |
| 52 | Анализ к/р. Предмет
стереометрия. Многогранник. Призма | 1 | Урок-
беседа | 1) Предмет
стереометрии. 2) Геометрические тела и поверхности. 3) Многогранники. 4) Вершины, грани, диагонали многогранника. 5) Призма | Знать: сведения о телах и поверхностях в пространстве, определения многогранника, W-угольной призмы. Уметь: изображать многогранники и распознавать их |
|
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 53 | Параллелепипед | 1 | КУ | 1) Параллелепипед. 2) Прямой параллелепипед. 3) Прямоугольный параллелепипед. 4) Свойство
диагоналей
параллелепипеда. 5) Виды сечений параллелепипеда | Знать: определения. Уметь: строить сечения параллелепипеда |
|
|
|
| 54 | Объем тела. Свойства прямоугольного параллелепипеда | 1 | УОНМ | 1) Понятие объема. 2) Свойства объемов. 3) Принцип
Кавальери. 4) Свойства прямоугольного параллелепипеда. 5) Объем прямоугольного параллелепипеда. 6) Объем призмы | Знать: свойства объемов тел, свойства прямоугольного параллелепипеда, формулы для вычисления объема прямоугольного параллелепипеда и призмы; в чем заключается принцип Кавальери. Уметь: находить объем прямоугольного параллелепипеда и призмы |
|
|
|
| 55 | Пирамида | 1 | КУ | 1) Пирамида. 2) Правильная пирамида. 3) Высота и апофема пирамиды. 4) Объем пирамиды | Знать: какой многогранник называется пирамидой, какая пирамида является правильной; что такое высота и апофема пирамиды; формулу для вычисления объема пирамиды. Уметь: изображать и распознавать пирамиду и строить сечения; находить объем пирамиды | Площадь боковой поверхности правильной пирамиды |
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 56 | Цилиндр | 1 | КУ | 1) Цилиндр. 2) Боковая
поверхность цилиндра. 3) Развертка
боковой поверхности. 4) Формулы объема и площади поверхности цилиндра | Знать: какое тело называется цилиндром; что такое ось, высота, основания, радиус, боковая поверхность, образующие цилиндра; формулу объема цилиндра; формулу площади боковой поверхности цилиндра. Уметь: объяснять, как получается развертка боковой поверхности
цилиндра; использовать формулы объема цилиндра и площади боковой поверхности при решении задач; изображать и распознавать на чертеже | Наклонный цилиндр |
|
|
| 57 | Конус | 1 | КУ | 1) Конус. 2) Ось, высота, основание, образующая боковая поверхность конуса. 3) Формулы объема конуса и площади боковой поверхности конуса | Знать: какое тело называется конусом; что такое ось, высота, основание, боковая поверхность, образующие конуса; что представляет собой развертка боковой поверхности конуса; формулы объема и площади боковой поверхности конуса. Уметь: распознавать и изображать конус; применять формулы при вычислении объема и площади боковой поверхности конуса | Вывод формулы для вычисления объема конуса |
|
|
| 58 | Сфера и шар | 1 | КУ | 1) Сфера. Шар. 2) Центр, радиус, диаметр сферы. 3) Объем шара. 4) Площадь сферы | Знать: что называется сферой и что такое ее центр, радиус, диаметр; какое тело называется
шаром; формулы объема шара и площади сферы. Уметь: распознавать и изображать на чертеже; вычислять объем шара и площадь сфер | Вывод
формулы объема шара |
|
|
Продолжение табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Аксиомы планиметрии (2 ч) |
| 59 | Об аксиомах планиметрии | 1 | КУ | 1) Аксиоматический метод. 2) Система аксиом | Знать: неопределенные понятия и систему аксиом как необходимые утверждения при создании геометрии |
|
|
|
| 60 | Об аксиомах планиметрии | 1 | Урок-
беседа | Система
аксиом | Знать: основные аксиомы планиметрии, иметь представление об основных этапах развития геометрии |
|
|
|
| Итоговое повторение (8 ч) |
| 61 | Повторение темы «Параллельные прямые» | 1 | УОСЗ | Признаки параллельности прямых | Знать: свойства и признаки параллельных прямых. Уметь: решать задачи по данной теме, выполнять чертежи по условию задач |
|
|
|
| 62 | Повторение темы «Треугольники» | 1 | УПЗУ | Равенство и подобие треугольников, сумма углов треугольников, равнобедренный треугольник, прямоугольный треугольник, формулы, выражающие площадь треугольника: через 2 стороны и угол между ними, через периметр и радиус вписанной окружности, формула Герона | Знать и уметь: применять при решении задач основные соотношения между сторонами
и углами треугольника; формулы площади треугольника |
|
|
|
Окончание табл.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 63 | Повторение темы «Окружность» | 1 | УПЗУ | 1) Окружность и круг. 2) Касательная и окружность. 3) Окружность, описанная около треугольника и вписанная в треугольник | Знать: формулы длины окружности и дуги, площади круга и сектора. Уметь: решать геометрические задачи, опираясь на свойства касательных к окружности, применяя дополнительные построения, алгебраический и тригонометрический аппарат |
|
|
|
| 64 | Повторение темы «Четырехугольники» | 1 | УОСЗ | Прямоугольник, ромб,
квадрат,
трапеция | Знать: виды четырехугольников и их свойства, формулы площадей. Уметь: выполнять
чертеж по условию задачи, решать простейшие задачи по теме «Четырехугольники» |
|
|
|
| 65 | Повторение темы «Четырехугольники, многоугольники» | 1 | УПЗУ | 1) Четырехугольник, вписанный и описанный около окружности. 2) Правильные многоугольники | Знать: свойства сторон четырехугольника, описанного около окружности; свойство углов вписанного четырехугольника. Уметь: решать задачи, опираясь на эти свойства | Площадь четырехугольника |
|
|
| 66 | Повторение темы «Векторы. Метод координат» | 1 | УПЗУ | 1) Вектор, длина вектора. 2) Сложение векторов, свойства сложения. 3) Умножение вектора на число и его свойства. 4) Коллинеарные векторы | Уметь: проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами |
|
|
|
| 67 |
| 1 | КУ | Контроль знаний и умений | Использовать
приобретенные знания и умения в практической деятельности для решения практических задач, связанных с нахождением геометрических величин |
|
|
|
| 68 | Подведение итогов | 1 |
|
|
|
|
|
|
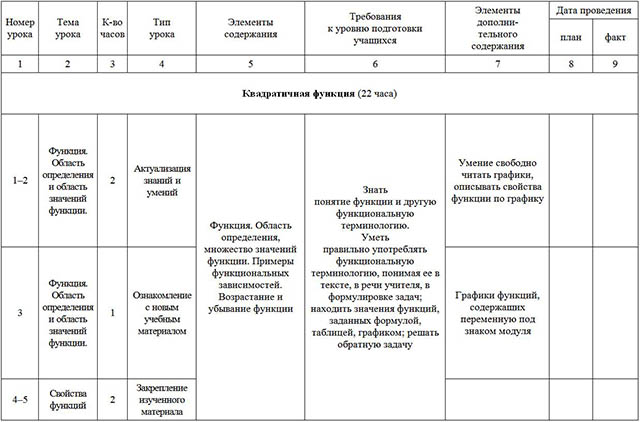
![]() 0.
0.
 Получите свидетельство
Получите свидетельство Вход
Вход


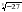 ,
, 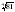 . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется. 0.
0.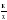 , у=
, у=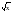 , у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;
, у=ах2+bх+с, у= ах2+n у= а(х - m) 2 ), строить их графики;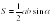 .
.








 Календарно-тематическое планирование по математике (9 класс) (0.14 MB)
Календарно-тематическое планирование по математике (9 класс) (0.14 MB)
 0
0 6266
6266 1139
1139 Нравится
0
Нравится
0




