Министерство образования Республики Саха (Якутия)
Муниципальное учреждение «Управление образования»
МР «Горный улус» Республики Саха (Якутия)
МБОУ «Бердигестяхская улусная гимназия»
«Согласовано» «Утверждаю»
Зам директора по УВР Директор МОУ «БУГ»
____________/Филиппова Н. В./ ___________/Агеева Л. П./
2012 г. 2012 г.
Спец-курс по алгебре на тему:
«Дополнительные вопросы математики в 9 классе»
Класс: 9
Учитель: Михайлова Ирина Кирилловна
Количество часов: 34
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Материалы Единого государственного экзамена, конкурсные задачи в ВУЗы содержат «нестандартные задачи, такие задачи, хотя и сформулированы с использованием только обычных понятий элементарной математики, тем не менее, не могут быть решены с помощью стандартных приемов. Методы решения таких задач недостаточно рассматриваются в курсе обучения математики. Поэтому выходом их создавшегося положения может служить продолжение изучения дополнительных вопросов алгебры в рамках соответствующего спецкурса. Вышесказанным объясняется актуальность и необходимость разработки и апробации данного курса. Итак, основной целью данного спецкурса является углубление и расширение знаний учащихся по математике.
Цель курса:
формирование представления о монотонных, четных, нечетных, ограниченных, неограниченных, кусочно-заданных функциях, применение их свойств для построения графиков и решения задач повышенной сложности;
формирование представления о числовых последовательностях, о арифметической и геометрической прогрессиях,
формирование умений решать уравнения и неравенства с одной переменной, их системы с двумя и более переменными, и неравенства с двумя переменными, содержащими знак модуля.
формирование умений решать задачи по теории вероятностей.
Задачи курса:
- повысить уровень математического и логического мышления обучающихся;
- способствовать приобретению исследовательских компетенций в решении математических задач;
- развить интерес и положительную мотивацию изучения математики;
- дать ученику возможность реализовывать свои интеллектуальные и творческие способности.
Сроки реализации образовательной программы, формы и режим занятий, ожидаемые результаты, способы их проверки:
Содержание программы спецкурса составлено с учетом возрастных особенностей учащихся 9 класса: лекционная система обучения, решение проблемных заданий, выдвижение собственных гипотез, проблем, нахождение своих путей решения, работа над понятиями и научными терминами, выявление различных способов решения задач и выбора наиболее рационального, анализ.
В целях контроля знаний по окончании изучения каждой темы учащиеся выполняют задания в форме тестов.
Система обучения по программе — 34 часа, 1 час в неделю.
Срок реализации программы — в течение всего учебного года.
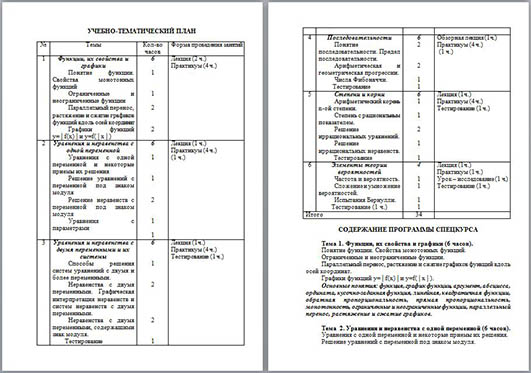
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
| № | Темы | Кол-во часов | Форма проведения занятий |
| 1 | Функции, их свойства и графики Понятие функции. Свойства монотонных функций Ограниченные и неограниченные функции Параллельный перенос, растяжение и сжатие графиков функций вдоль осей координат Графики функций у=│f(x)│и у=f(│x│) | 6
1
1
2
2 | Лекция (2 ч.) Практикум (4 ч.) |
| 2 | Уравнения и неравенства с одной переменной Уравнения с одной переменной и некоторые приемы их решения Решение уравнений с переменной под знаком модуля Решение неравенств с переменной под знаком модуля Уравнения с параметрами | 6
1
1
2
1
1 | Лекция (1 ч.) Практикум (4 ч.) (1 ч.) |
| 3 | Уравнения и неравенства с двумя переменными и их системы Способы решения систем уравнений с двумя и более переменными. Неравенства с двумя переменными. Графическая интерпретация неравенств и систем неравенств с двумя переменными. Неравенства с двумя переменными, содержащими знак модуля. Тестирование
| 6
1
2
2
1 | Лекция (1ч.) Практикум (4 ч.) Тестирование (1 ч.) |
| 4 | Последовательности Понятие последовательности. Предел последовательности. Арифметическая и геометрическая прогрессии. Числа Фибоначчи. Тестирование | 6 2
2
1 1 | Обзорная лекция (1ч.) Практикум (4 ч.) (1 ч.) |
| 5 | Степени и корни Арифметический корень n-ой степени. Степень с рациональным показателем. Решение иррациональных уравнений. Решение иррациональных неравенств. Тестирование | 6 1
1
2
1
1 | Лекция (1ч.) Практикум (4 ч.) Тестирование (1 ч.) |
| 6 | Элементы теории вероятностей Частота и вероятность. Сложение и умножение вероятностей. Испытания Бернулли. Тестирование (1 ч.) | 4
1 1
1 1 | Лекция (1ч.) Практикум (1 ч.) Урок – исследование (1 ч.) Тестирование (1 ч.) |
| Итого | 34 |
|
СОДЕРЖАНИЕ ПРОГРАММЫ СПЕЦКУРСА
Тема 1. Функции, их свойства и графики (6 часов).
Понятие функции. Свойства монотонных функций.
Ограниченные и неограниченные функции.
Параллельный перенос, растяжение и сжатие графиков функций вдоль осей координат.
Графики функций у=│f(x)│и у=f(│x│).
Основные понятия: функция, график функции, аргумент, абсцисса, ордината, кусочно-заданная функция, линейная, квадратичная функции, обратная пропорциональность, прямая пропорциональность, монотонность, ограниченные и неограниченные функции, параллельный перенос, растяжение и сжатие графиков.
Тема 2. Уравнения и неравенства с одной переменной (6 часов).
Уравнения с одной переменной и некоторые приемы их решения.
Решение уравнений с переменной под знаком модуля.
Решение неравенств с переменной под знаком модуля.
Уравнения с параметрами.
Основные понятия: квадратный трехчлен, корни квадратного трехчлена, разложение на множители, квадратные уравнения, неполные квадратные уравнения, приведенное квадратное уравнение, параметр, дробно-рациональные уравнения, корни уравнения, параметр.
Тема 3. Уравнения и неравенства с двумя переменными и их системы (6 часов).
Способы решения систем уравнений с двумя и более переменными.
Неравенства с двумя переменными. Графическая интерпретация неравенств и систем неравенств с двумя переменными.
Неравенства с двумя переменными, содержащими знак модуля.
Основные понятия: уравнения, равносильные уравнения, степень уравнения, график уравнения с двумя переменными, графический способ решения систем уравнений и неравенств, симметрические многочлены.
Тема 4. Последовательности (6 часов).
Понятие последовательности. Предел последовательности.
Арифметическая и геометрическая прогрессии.
Числа Фибоначчи.
Основные понятия: возрастающая, убывающая, ограниченная, неограниченная, сходящаяся последовательности, прогрессия, предел последовательности.
Тема 5. Степени и корни (6 часов).
Арифметический корень n-ой степени.
Степень с рациональным показателем.
Решение иррациональных уравнений.
Решение иррациональных неравенств.
Основные понятия: корни n-ой степени, свойства корней, двойной радикал, допустимые значения переменной, иррациональные уравнения и неравенства и их решения.
Тема 6. Элементы теории вероятностей (4 часа).
Частота и вероятность.
Сложение и умножение вероятностей.
Испытания Бернулли.
Основные понятия: случайное событие, частота случайного события, благоприятный исход, вероятность, несовместные события, независимые события.
МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРОГРАММЫ СПЕЦКУРСА
Тема 1. Функции, их свойства и графики.
Цели:
сформировать представление о монотонных, четных, нечетных, ограниченных, неограниченных, кусочно-заданных функциях;
применение свойств функций для построения графиков и решения задач повышенной сложности.
Форма проведения: Лекция (2 ч), Практикум (4 ч).
Тема 2: Уравнения и неравенства с одной переменной.
Цели:
Форма проведения: лекция (1 ч), практикум (4 ч), тестирование (1 ч).
Тема 3: Уравнения и неравенства с двумя переменными и их системы
Цели:
рассмотреть способы решения систем уравнений с двумя и более переменными;
сформировать представление о графическая интерпретация неравенств и систем неравенств с двумя переменными
рассмотреть метод замены переменной и метод интервалов при решении неравенств.
Форма проведения: лекция (1ч), практикум (4 ч), тестирование (1 ч).
Тема 4: Последовательности.
Цели:
Форма проведения: обзорная лекция (1ч), практикум (4 ч), тестирование (1 ч).
Тема 5: Степени и корни.
Цели:
Форма проведения: лекция (1ч), практикум (4 ч), тестирование (1 ч).
Тема 6: Элементы теории вероятностей.
Цели:
сформировать понятия случайное событие, частота случайного события, благоприятный исход, несовместные события, независимые события;
рассмотреть способы нахождения частоты и вероятности события при решении задач.
Форма проведения: лекция (1ч.), практикум (1 ч), урок-исследование (1 ч), тестирование (1 ч).
ЛИТЕРАТУРА
Макарычев Ю.Н. Алгебра. 9 класс: учеб. для 9 кл. общеобразоват. учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов.– 7-е изд., испр. и доп..– М.: Мнемозина, 2008.
Глазков Ю.А. Тесты по алгебре: 9 класс: к учебнику Ю.Н. Макарычева и др. «Алгебра. 9 класс» / Ю.А. Глазков, М.Я. Гаишвили. – М.: Экзамен, 2011.
Дидактические материалы по математике для классов с углубленным изучением математики.
Н.Я. Виленкин и др. Алгебра учебник для учащихся 9 класса с углубленным изучением математики. М. «Просвещение» 2003 г.
Математика. 9 класс. Подготовка к ГИА-2011: учебно-методическое пособие/ Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион-М, 2010.
Математика. 9-11 класс. Задания. Решения и рекомендации- 2014г.
Математика. Тематические тесты. 9 класс для подготовки к ЕГЭ. Под ред Ф.Ф Лысенко, Кулабухова С.Ю-2014г.
8. Математика . ГИА -9 в форме ОГЭ под ред. Лысенко Ф.Ф, С.Ю , Кулабухова -2014г

 Получите свидетельство
Получите свидетельство Вход
Вход












 Спецкурс по алгебре на тему «Дополнительные вопросы математики в 9 классе» (27.36 КB)
Спецкурс по алгебре на тему «Дополнительные вопросы математики в 9 классе» (27.36 КB)
 0
0 996
996 100
100 Нравится
0
Нравится
0



