Производная

Цели урока:

Обучающие:  систематизировать знания и умения по теме «Производная»: формулы и правила дифференцирования, геометрический и физический смысл производной

Развивающие:  развивать творческую и мыслительную деятельность учащихся, способность к «видению» проблемы, формировать умения чётко и ясно излагать свои мысли.

Воспитательные: воспитывать умение работать с имеющейся информацией, слушать товарищей, точно, однозначно и лаконично формулировать свои ответы.

1) Как называется нахождение производной данной функции f ?

2) Как называется точка, в которой производная меняет знак с «+» на «-» ?

3) Переменная x в задании функции y = - 3x + 4?

4) Какой ученый ввел термин производная»?

5) Как называется прямая, проходящая через т.(x0; f(x0)) и имеющая угловой коэффициент f ' (x0)?

Тема урока :

Обобщающий урок по теме: «Производная и ее применение»

Разработала:

учитель математики

Куш ни ренко Домн икия Николаевна

2012 г.

Цели урока:

• Обучающие: систематизировать знания и умения по теме «Производная»: формулы и правила дифференцирования, геометрический и физический смысл производной
• Развивающие: развивать творческую и мыслительную деятельность учащихся, способность к «видению» проблемы, формировать умения чётко и ясно излагать свои мысли.
• Воспитательные: воспитывать умение работать с имеющейся информацией, слушать товарищей, точно, однозначно и лаконично формулировать свои ответы

Эта

удивительная

производная!

• « Музыка может возвышать или умиротворять душу,
• живопись – радовать глаз,
• поэзия – пробуждать чувства,
• философия – удовлетворять потребности разума,

• инженерное дело – совершенствовать материальную сторону жизни людей,

• а математика способна достичь всех этих целей!»
• Морис Клайн

« Знания имей отличные, решая задачи различные».

• 1) Как называется нахождение производной данной функции f ?
• 2) Как называется точка, в которой производная меняет знак с «+» на «-» ?
• 3) Переменная x в задании функции

y = - 3 x + 4?

• 4) Какой ученый ввел термин производная»?

• 5) Как называется прямая, проходящая через т.( x 0 ; f ( x 0 )) и имеющая угловой коэффициент f ' ( x 0 )?

1

f(x) = 2 x 4 - 2x 3 + 3х + 4

2

f(x) = x 4 + 7x

3

f′(1)

4

f(x) = 5x 3 + 7

f′(0)

f(x) = x 8 + 2x 2

5

f′(2)

f′( 1 )

f(x) = 2 x 4 + x

6

7

f(x) = x 9

f′(1)

f(x) = 4x 3 + 2x 2 +3x

f′(1)

f′( 0 )

№

Ответ

1

Шифр

2

  5

3

Л

  7

4

А

  60

Г

  12

5

Р

  7

6

  9

7

А

  3

Н

Ж

2 м

а

к

с

1 д

3 а

и

м

р

ф

г

у

ф

м

у

е

м

р

е

н

4 Л

н

т

а

ц

г

и

р

о

а

5 к

а

н

в

ж

с

а

а

н

т

и

е

л

ь

н

а

я

Тест № 1 Найдите производные следующих функций и выберите правильный ответ из предложенных:

• 1. Y= 7 x 5
• a) 12x ; б ) 35x 4 ; в ) 35x 5
• 2 . Y = 0,5 x 4 + x
• a ) 2 x 3 +1 ; б) 4,5 x 3 +1; в) 2 x 3 + x
• 3 . y =
• a ) x 3 ; б) 16 x 4 ; в)
• 4. у= sinx +1
• a) cosx+1; б ) -cosx ; в ) cosx
• 5. y= x 6 +3
• a) 6x5+ ; б ) 6x 5 + ; в ) 6x5+6
• 6. y =
• a) - б ) - ; в )
• y = 5sin 3 х
• a ) 15 sin 2 x б) 15 sin 2 x cosx ; в) 15 sin 3 x cosx

Тест № 2 по теме

«Производная и ее применение».

II вариант

I вариант

1). Напишите уравнение

касательной к графику

функции

в точке с абсциссой

1). Напишите уравнение

касательной к графику

функции

в точке с абсциссой

а). y=10x+12 в). y=2x-6

б). y=- 4x+7 г). y=4x-7

а). y=13x+6 в). y= 2x+13

б). y=- x+3 г). y=-6x-13

2 ) . Найти промежутки

возрастания функции

2 ) . Найти промежутки

убывания функции

а). в).

б). г).

а). в).

б). г).

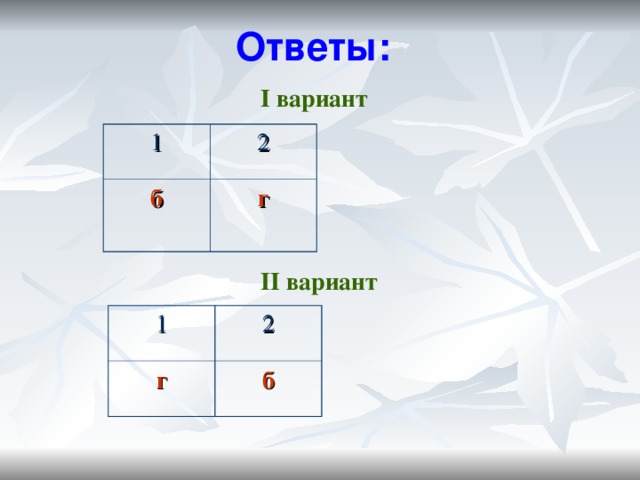
Ответы:

I вариант

1

2

б

г

II вариант

1

г

2

б

Найдите ошибку в вычислении производной:

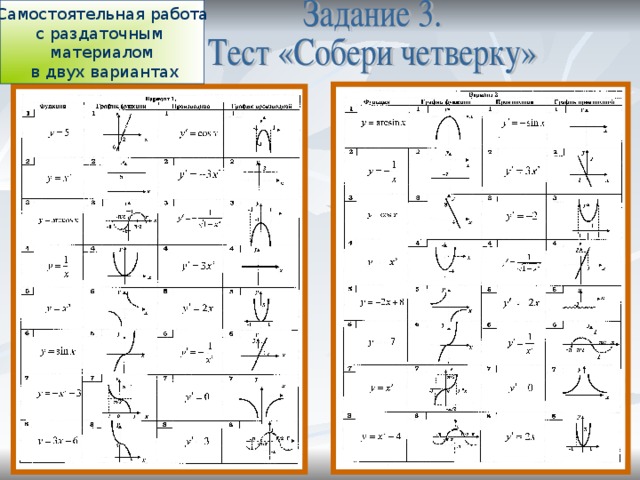
Самостоятельная работа

с раздаточным

материалом

в двух вариантах

Самопроверка. Правильные ответы:

2 вариант

• 1-7-4-3
• 2-5-6-7
• 3-8-1-6
• 4-1-5-2
• 5-3-3-5
• 6-2-7-1
• 7-6-2-8
• 8-4-8-4

1 вариант

• 1-2-7-4
• 2-4-5-6
• 3-7-3-3
• 4-5-6-7
• 5-6-4-5
• 6-3-1-8
• 7-8-2-1
• 8-1-8-2

Результаты теста внесите в оценочный лист!

Задача № 1

Материальная точка движется прямолинейно по закону

x (t) = 6 t² - 48 t +17 , где Х – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t =9c.

  .

Задача № 2

Материальная точка движется прямолинейно по закону

x (t)=t² -13t + 23. где х – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с ?

задачи № 1

Решение

• Найдем производную функции  x (t) = 6 t² - 48 t +17

x’ (t) = 12t – 48

2. Найдем значение производной в точке

t = 9  

x’ (9) = 12 x 9 – 48

x’ (9) = 60

:

:

Ответ: 60 м/с.

Задача № 2

• Решение.
• Если нам известна скорость точки в некий момент времени, следовательно нам известно значение производной в точке t  .
• Найдем производную функции
• x (t)=t² -13t + 23
• x’ (t) = 2t – 13
• По условию, скорость точки равна 3 м/с, значит, значение производной в момент времени  t равно 3.
• Получаем уравнение: x’ (t) = 2t – 13 =3
• Отсюда   t =8 с.
• Ответ: 8 с

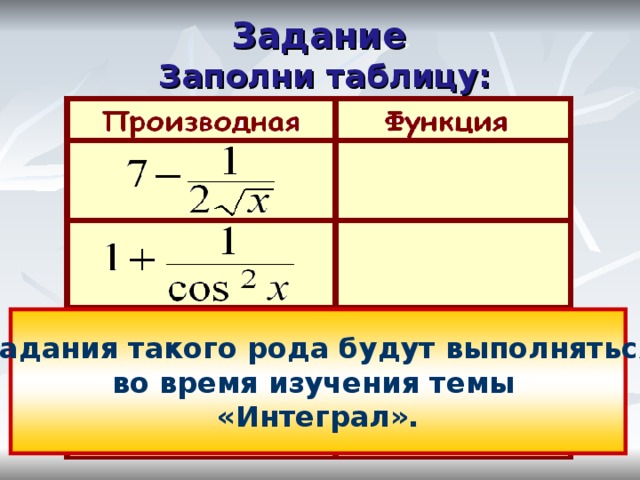
Задание Заполни таблицу:

Задания такого рода будут выполняться

во время изучения темы

«Интеграл».

Подводим итоги урока:

• Вспомните, каковы были цели, поставленные нами в начале урока?
• Достигнуты ли цели?
• Что удалось?
• Что не получилось?
• Понравился ли вам урок?