Урок по теме «Применение производной в различных областях науки»
11 класс
Составила учитель математики МБОУ СОШ №8»
Середа Татьяна Юрьевна
Цели:
Обучающие цели:
обеспечить повторение учащимися изученного материала, наиболее общих и существенных понятий, теорем и алгоритмов.
предоставить учащимся возможность использовать приобретенные знания при решении задач разного содержания и уровня сложности.
обеспечить проверку усвоения учащимися изученного материала.
Воспитательные цели:
обучать объективной оценке своих возможностей и успехов;
формировать навыки работы в заданном темпе;
способствовать развитие навыков устной речи, умения грамотно вести диалог и аргументировать свои действия;
Интеллектуально-развивающие цели:
создать условия для развития наблюдательности, памяти и внимания учащихся;
способствовать развитию навыков работы с большими объемами информации: поиску, отбору, анализу, оформлению необходимого материала;
создать условия для проявлений творческого подхода к учебным задачам, выдвижению гипотез, постановке проблем и поиску путей их решения;
обучать методам научного познания - анализу, сравнению, обобщению и систематизации учебного материала
Оборудование:
Мультимедийный проектор.
Презентации учащихся.
Раздаточный материал
Девиз урока: «Решай, ищи, твори и мысли»
Замечание. За 1 неделю до урока класс разделен на 4 группы и назначены консультанты. В группу вошли учащиеся с разными учебными возможностями. Каждая группа получила задание приготовить презентацию «Применение производной для решения задач из различных областей науки».
1 группа – «Исторические сведения»;
2 группа - «Применение физического смысла производной при решении физических задач»;
3 группа – «Применение производной в химии и биологии»
4 группа - «Решение задач с географическим, экономическим содержанием».
На подготовительном периоде и в ходе урока консультанты руководят работой группы: распределяют обязанности между учениками, организуют консультации с учителями предметниками.
ПЛАН УРОКА
I. ОРГАНИЗАЦИОННЫЙ ЭТАП.
Показатели выполнения психологической задачи этапа:
доброжелательный настрой учителя и учащихся;
быстрое включение класса в деловой ритм;
организация внимания всех учащихся;
кратковременность организационного момента;
полная готовность класса и оборудования к работе.
Урок по теме «Применение производной в различных областях науки». Урок проводится после изучения производных элементарных функций. Форма организации учебной деятельности групповая. При актуализации знаний предлагаются задания из ЕГЭ. Часть урока отводится презентациям, выполненным самими учащимися: «Применение физического смысла производной при решении физических задач», «Решение химических и биологических задач с помощью производной», «Решение задач с географическим, экономическим содержанием».
II. ВСУПИТЕЛЬНОЕ СЛОВО УЧИТЕЛЯ И УСТНЫЙ СЧЕТ.
Здравствуйте. (Откройте тетради. Запишите число, классная работа, тему урока.) Тема нашего урока «Применение производной в различных областях науки». И сегодня мы попытаемся, насколько это возможно, в рамках одного урока рассмотреть эту тему. Эпиграфом к нашему уроку хочу взять слова Лобачевского:
«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…»
Н.И. Лобачевский
Активизация знаний учащихся На одном из первых уроков изучения производной я вам задала вопрос:
Мы изучаем производную. А так ли это важно в жизни?
Вы на него не смогли ответить, т.к. у вас не хватило соответствующих знаний. И тогда я вам предложила поработать над проектами, т.е. провести самостоятельное исследование по теме «Производная и её применение в различных областях науки».
Вам было предложено 4 темы. И сегодня мы увидим насколько успешно вы справились с задачей самостоятельного отбора и перерабатывания информации.
А чтобы у вас была путеводная звезда, к которой бы вы шли, я выдвинула гипотезу /читаю гипотезу, /
«Дифференциальное исчисление- это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.»
В ходе исследовательской работы вы должны были либо подтвердить, либо опровергнуть данную гипотезу.
Но прежде, чем мы перейдем к вашим проектам, мы проведем устную подготовительную работу.
Раз уж мы говорим сегодня о производной, то наверно необходимо сначала вспомнить
Что называется производной функции в точке?
Ответ: производной функции у = f(x) в точке х0 называется предел отношения
приращения функции в точке х0 к приращению аргумента, когда последнее стремится к нулю.
Что необходимо знать для нахождения производной? Правила дифференцирования и таблицу производных.
| Вспомни! Ф.И. __________________________________________________ |
| Функция | Производная |
| kx+m | |
| | 2x |
| c,c - const | |
| 
| |
| | 
|
| 
| |
| | 
|
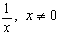
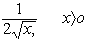
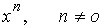
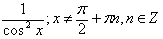
| sin x | |
| | 1 |
| ctg x | |
| | - sin x |
| k*f(x) | |
| | f'(x)+g'(x) |
| f(x)*g(x) | |
| |
|
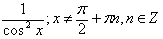
Задачи для устного счета предлагаются в виде презентаций.
1. Найти производные следующих функций и сопоставить их с ответами: (использование модуля MATHEM_3_2_1_3_2_k_b_1.0.0.12, http://fcior.edu.ru/)
Редакционная группа оценивает работу каждого по следующим критериям:
решил сам без ошибок и помог товарищу – 5 баллов
решил сам, но консультировался у товарища – 4 балла
решал с помощью карточки с формулами и учителя – 3 балла
На местах соответствующее задание выполняют учащиеся:
| Найдите производную функции:
| Ответы: |
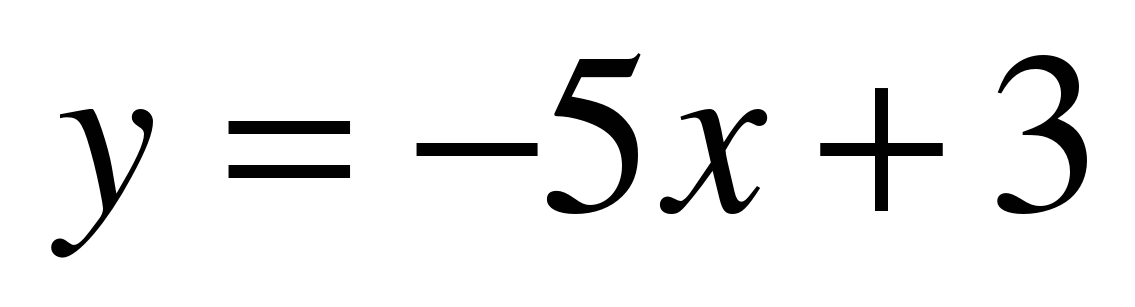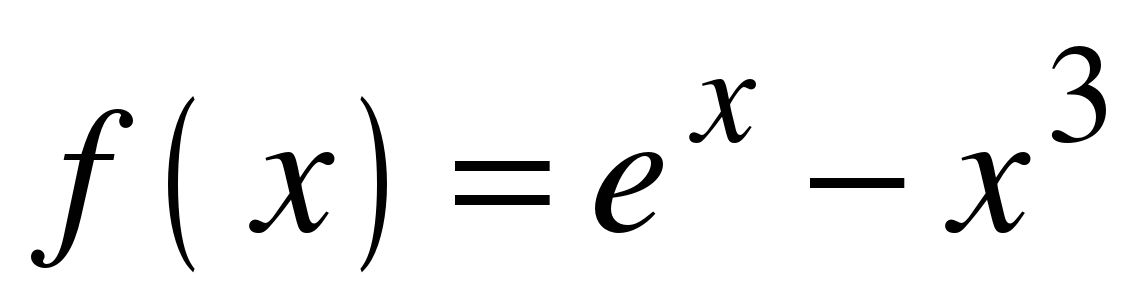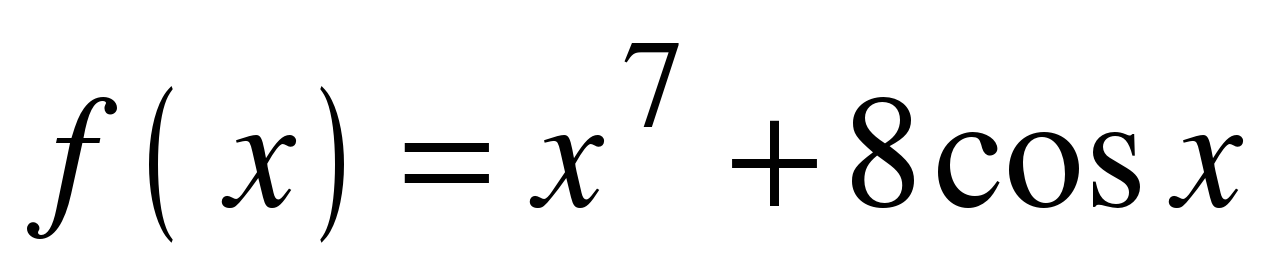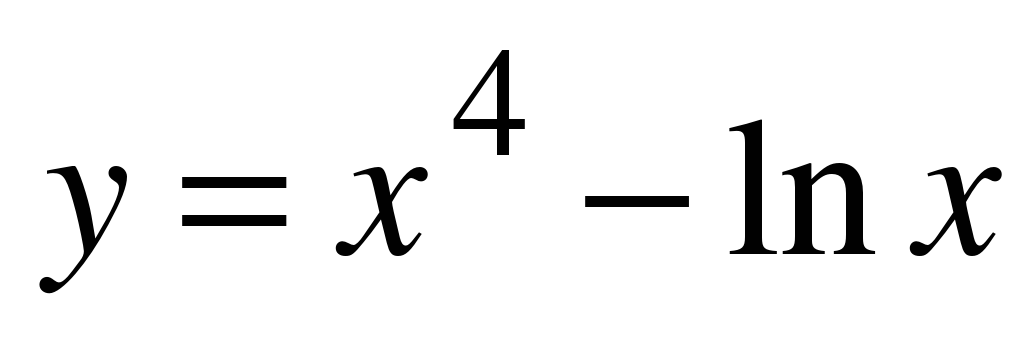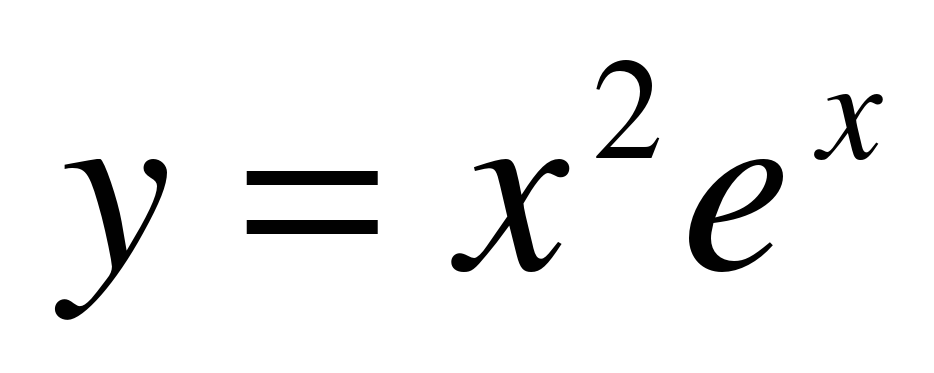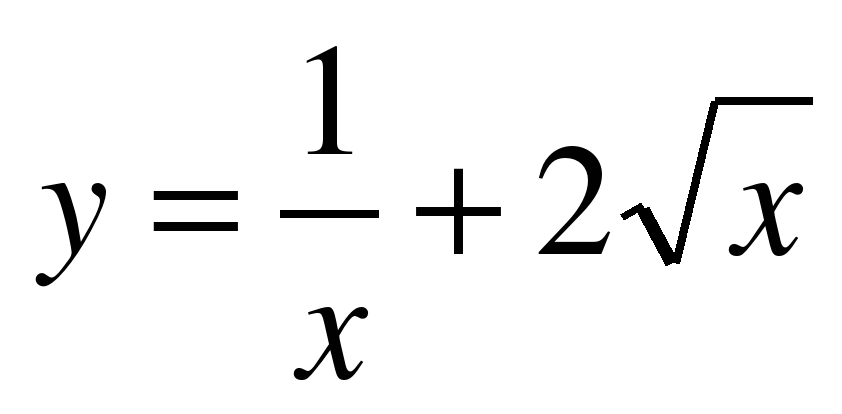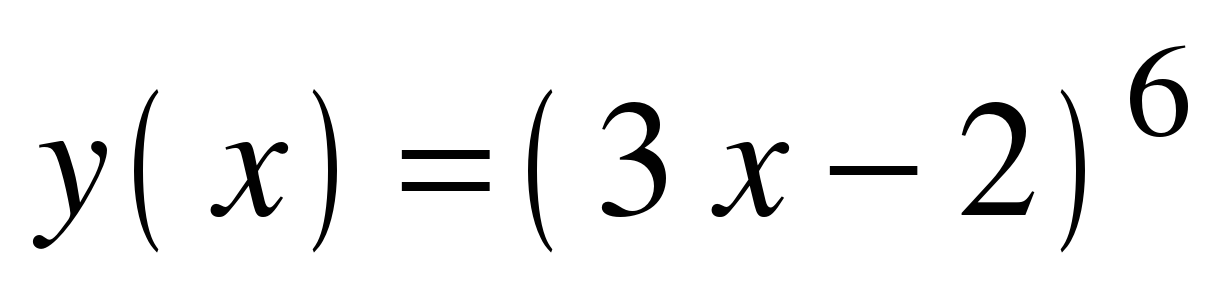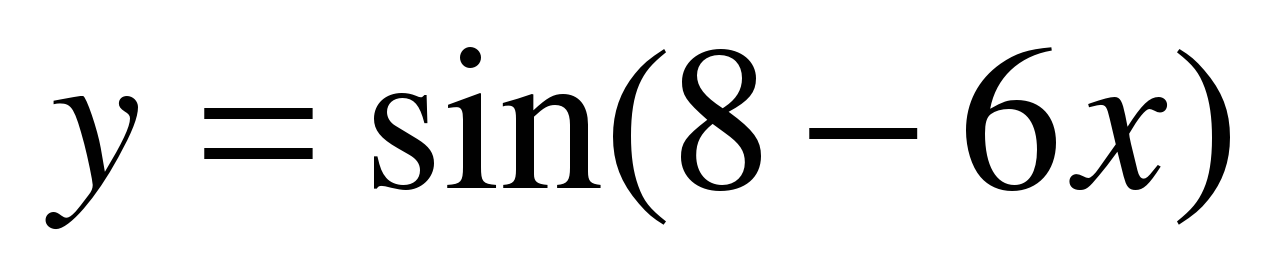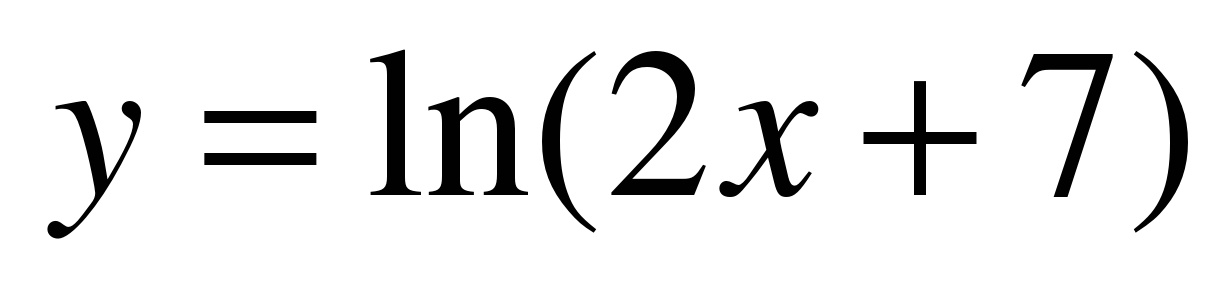         y = tg(5x) | f ′(x) = 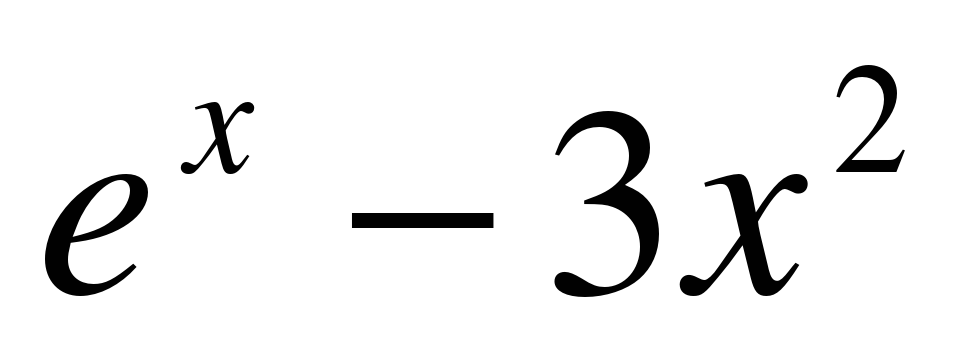 y′ = 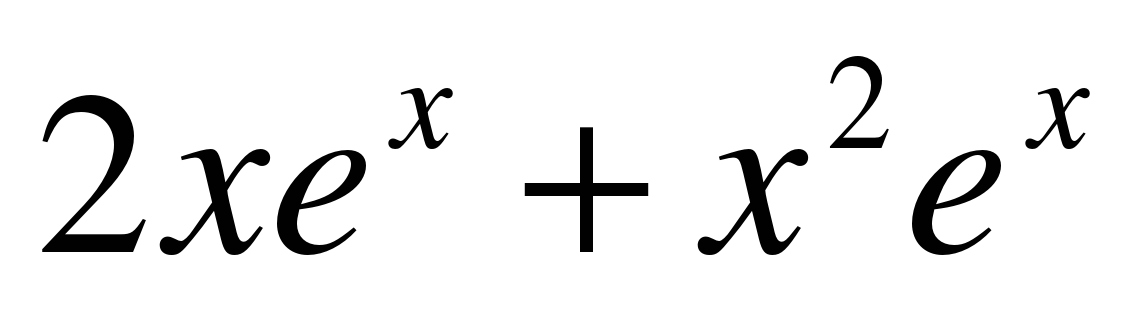 y′ = 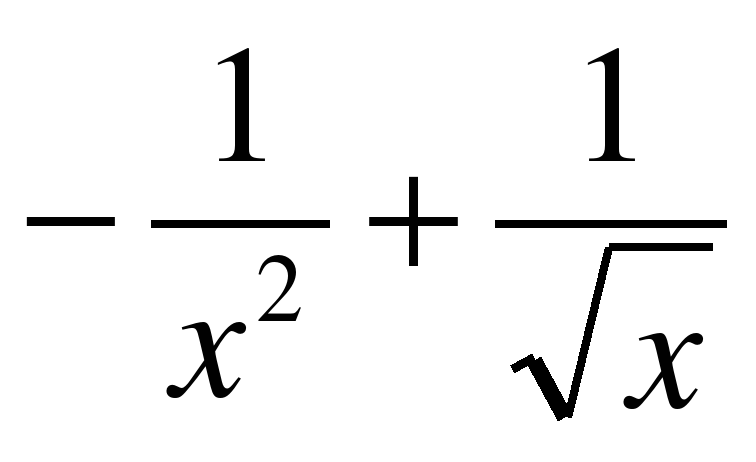 y′ = − 5 f ′(x) =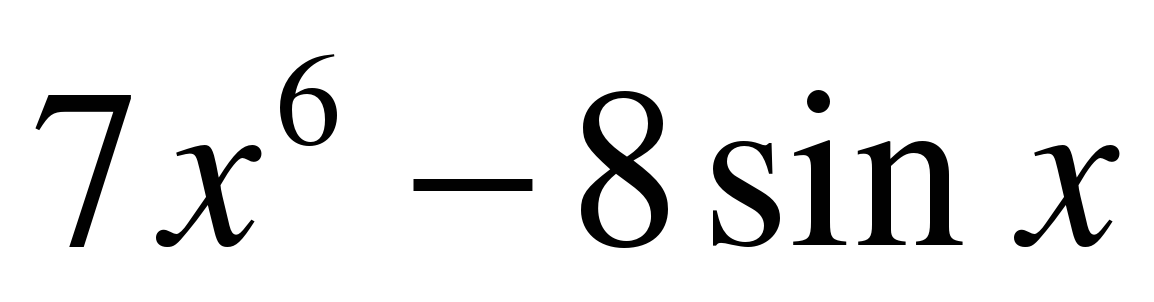 y′ = 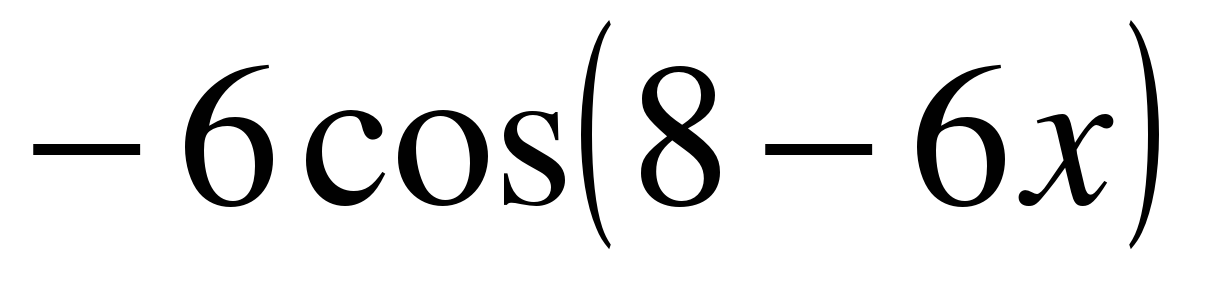 y′ = 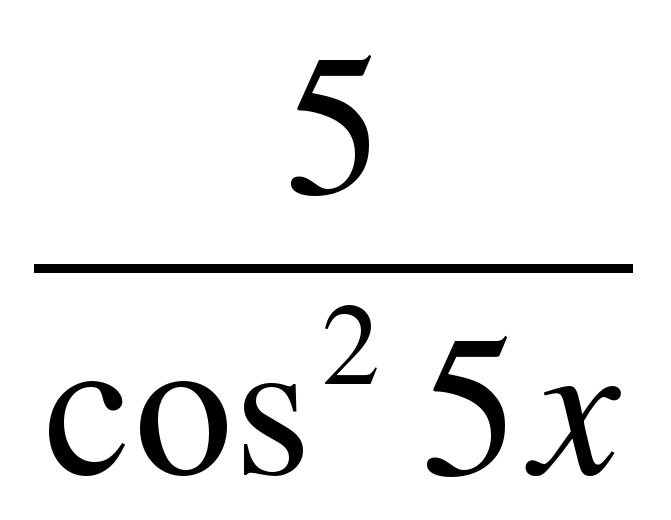 y ′= 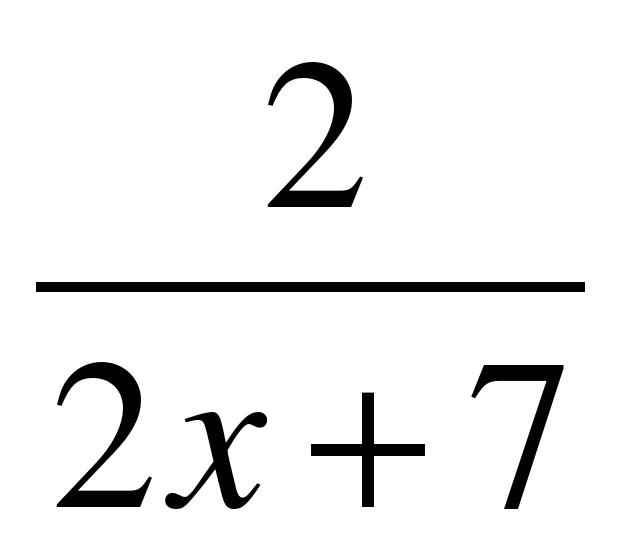 y′(x) = 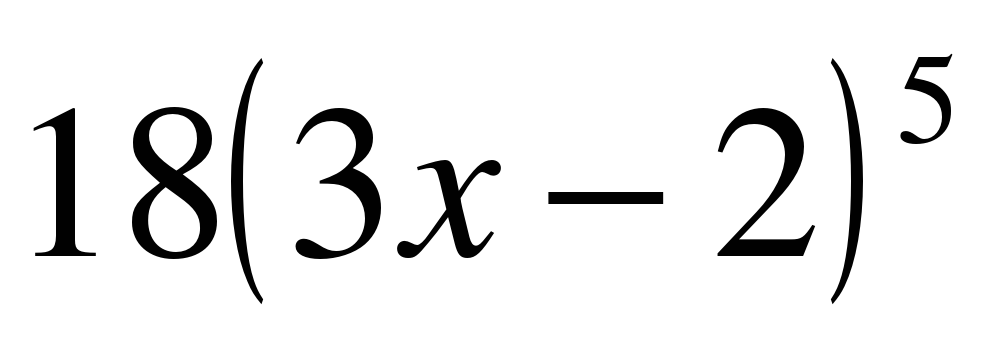 y′ =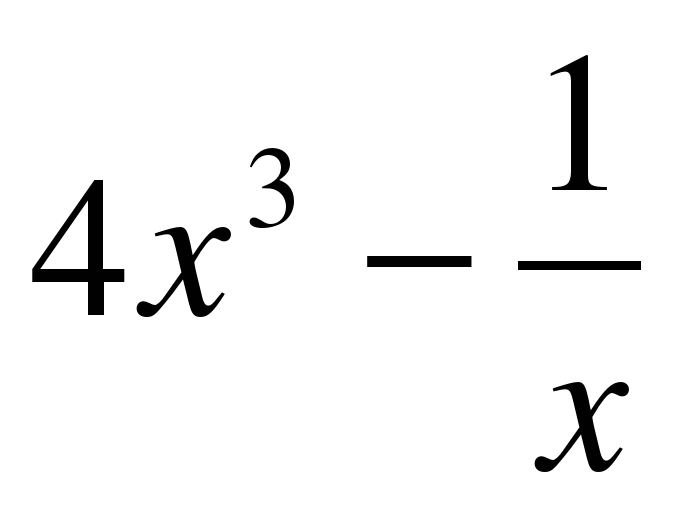 
|
III ПРОЕКТЫ УЧАЩИХСЯ.
А сейчас мы рассмотрим работы творческих групп, которые провели самостоятельные исследования по темам. Еще раз убедимся в важности роли производной в исследовании процессов окружающего мира, покажем практическую необходимость и теоретическую значимость темы "Производная".
I группа – «Исторические сведения»
Производная – одно из фундаментальных понятий математики.
Оно возникло в 18 веке. Независимо друг от друга И.Ньютон и
Г. Лейбниц разработали теорию дифференциального исчисления.
О Ньютоне.
Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон. А.Поуг.
Исаак Ньютон (1643-1727) один из создателей дифференциального исчисления.
Главный его труд- «Математические начала натуральной философии».- оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.
Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Интересно: Исаак Ньютон был так же и богословом. Он написал труды о Святой Троице, а также толкование на книгу пророка Даниила. Интересно, что он высоко ценил именно свои богословские сочинения. Всегда, произнося имя Божие, Ньютон снимал шляпу.
О Лейбнице
«Предупреждаю, чтобы остерегались отбрасывать dx,-ошибка, которую часто допускают и которая препятствует продвижению вперёд». Г.В.Лейбниц. (1646-1716)
Создатель Берлинской академии наук. Основоположник дифференци- ального исчисления, ввёл большую часть современной символики матема- тического анализа.
Лейбниц пришёл к понятию производной, решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл.
Но это не говорит о том, …
…что до них эти вопросы не изучались. Задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.
Эпизодически понятие касательной встречалось в работах итальянского математика И.Тартальи.
В 17в. на основе учения Г.Галилея активно развилась кинематическая концепция производной. Понятие производной встречается уже у Р.Декарта, французского математика Роберваля, английского учёного Д.Грегори, в работах И.Барроу.
Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс, Коши. Необходимо сказать, что ни Ньютон ни Лагранж не дали четкого определения производной. Впервые определение производной было сформулировано Коши, и именно это определение стало общепринятым и в настоящее время используется почти во всех курсах анализа.
II группа - «Применение физического смысла производной при решении физических задач».
Применение производной в физике очень обширно. Рассмотрим несколько примеров применения производной в физических задачах.
М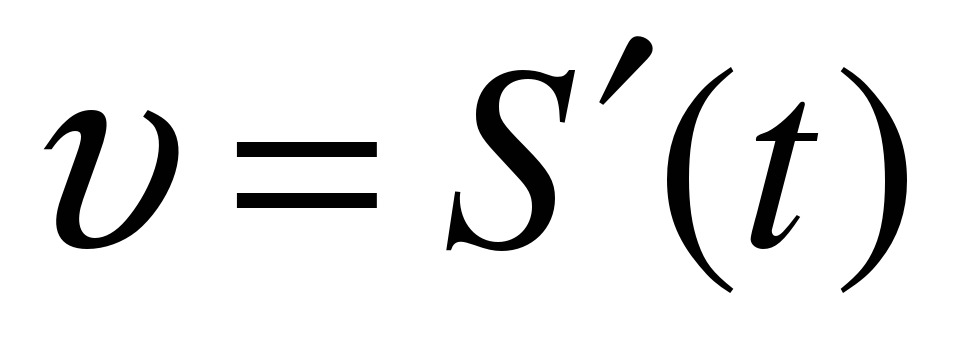
еханическое движение- это изменение положения тела в пространстве относительно других тел с течением времени.
Основной характеристикой механического движения служит скорость.
Алгоритм нахождения скорости тела с помощью производной.
Если закон движения тела задан уравнением s = s (t),
то для нахождения мгновенной скорости тела в какой-нибудь определенный момент времени надо:
1.Найти производную s' = f '(t).
2. Подставить в полученную формулу заданное значение времени.
Задание. Автомобиль приближается к мосту со скоростью 72 км/ч. У моста висит дорожный знак "36км/ч". За 7 сек до въезда на мост, водитель нажал на тормозную педаль. С разрешаемой ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой s=20t-t²
Да, т.к. скорость через 7 сек. будет равна 6м/с (21,6 км/ч).
Производная в электротехнике
В наших домах, на транспорте, на заводах : всюду работает электрический ток.
Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
В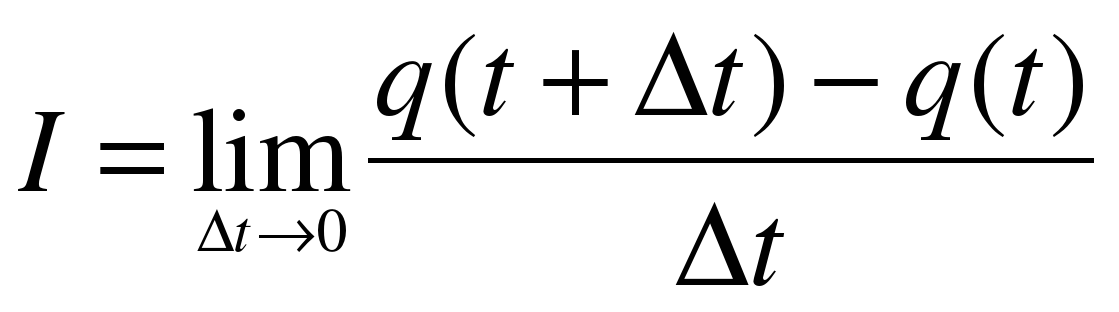
цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.
(Запишем)
В электротехнике в основном используется работа переменного тока.
Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.
Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.
(Запишем)
Задание
Заряд, протекающий через проводник , меняется по закону
Найти силу тока в момент времени t=5 cек.
Сила тока равна 2 А
А так же (Запишем):
Сила есть производная работы по перемещению,
т.е. F=A /(x)
Теплоемкость – есть производная теплоты по температуре, т.е. C(t) = Q/(t)
d(l)=m/(l) - линейная плотность
K (t) = l/(t) - коэффициент линейного расширения
ω (t)= φ/(t) - угловая скорость
а (t)= ω/(t) - угловое ускорение
N(t) = A/(t) - мощность
Задание: теплота.
1. Пусть Q (t) количество теплоты, которое необходимо для нагревания тела массой 1 кг от 00С до температуры t0 (по Цельсию), известно, что в диапазоне 00 до 950, формула Q (t) = 0,396t+2,08110-3t2-5,02410-7t3 дает хорошее приближение к истинному значению. Найдите, как зависит теплоёмкость воды от t.
Решение. C (t) = Q / (t) = 0,396 + 4,162*10 -3 t – 15,072*10 -7 t2
III группа - «Решение химических и биологических задач с помощью производной»;
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
Химия – это наука о веществах, о химических превращениях веществ.
Химия изучает закономерности протекания различных реакций.
Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.
Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.
Если C(t) – закон изменения количества вещества, вступившего в химическую реакцию, то скорость v(t) химической реакции в момент времени t равна производной: (Запишем)
| Понятие на языке химии | Обозначение | Понятие на языке математики |
| Количество в-ва в момент времени t0 | c = c(t) | Функция |
| Интервал времени | ∆t = t2 – t1 | Приращение аргумента |
| Изменение количества в-ва | ∆c = c(t+ t ) – c(t) | Приращение функции |
| Средняя скорость химической реакции | ∆c/∆t | Отношение приращён. функции к приращён. аргументу |
Предел этого отношения при стремлении Δt к нулю - есть скорость химической реакции в данный момент времени V (t) = c ‘(t)
Найти скорость реакции в момент времени t = 10сек, если концентрация исходного продукта меняется по закону 
Производная в биологии.
Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.
Задача по биологии.
По известной зависимости численности популяции x (t) определить относительный прирост в момент времени t.
| Понятие на языке биологии | Обозначение | Понятие на языке математики |
| Численность в момент времени t1 | x = x(t) | Функция |
| Интервал времени | ∆t = t2 – t1 | Приращение аргумента |
| Изменение численности популяции | ∆x = x(t2) – x(t1) | Приращение функции |
| Скорость изменения численности популяции | ∆x/∆t | Отношение приращения функции к приращению аргумента |
| Относительный прирост в данный момент | Lim ∆x/∆t t 0 | Производная |
IV группа - «Решение задач с географическим, экономическим содержанием».
Производная в географии.
Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t), 
. Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.
Выведем формулу для вычисления численности населения на ограниченной территории в момент времени t.
Пусть у = у(t)- численность населения.
Рассмотрим прирост населения за t = t-t0
y = k y t, где к = кр – кс –коэффициент прироста (кр – коэффициент рождаемости,
кс – коэффициент смертности)
y:t=k y
При t0 получим lim y/ t=у’
у’= к у (Запишем)
Производная в экономике. (Запишем)
П (t) = υ / (t) - производительность труда,
где υ (t) - объем продукции
J(x) = y / (x) - предельные издержки производства,
где y– издержки производства в зависимости от объема выпускаемой продукции x.
Задание.
Оборот предприятия за истекший год описывается через функцию U(t)=0,15t³ – 2t² + 200, где t – месяцы, U-миллионы.
Исследуйте оборот предприятия за 9 и 10 месяцы.
Решение. Исследуем оборот предприятия с помощью производной: U'(t)=0,45t² - 4t
Меньший оборот был на девятом месяце- 0,45. На 10 месяце -5.
Вывод. Что вы скажете о нашей гипотезе. Подтвердили мы ее или опровергли?
Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.
Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.
IV. ДОМАШНЯЯ РАБОТА .ИНСТПУКЦИЯ ПО ВЫПОЛНЕНИЮ.
Домашняя работа (долгосрочное на период изучения раздела, по мере изучения тем)
1
| уровень | задача | консультация |
|
А | 1. Тело движется по прямой согласно закону
s(t) = 1,5t2 – 3t + 7. В какой момент времени скорость тела будет равна 12? |
v(t) =, v(t) = 12. |
| 2. Объем продукции V цеха в течение дня зависит от времени по закону V(t) = -t3 + t2 + 50t + 70, где 1 ≤ t ≤ 8. Вычислите производительность труда П при t =7 ч. |
П (t) = V / (t) |
|
B | 3. Материальная точка массой 2кг движется прямолинейно по закону , где S– путь в метрах, t – время в секундах. Найдите силу, действующую на неё в момент t = 3 c.
|
, a(t) = |
| 4. Две материальные точки движутся прямолинейно по законам: В какой момент времени скорости их равны?
|
v1(t) = , v2(t) = , v1(t) = v2(t) |
|
C | 5. Цементный завод производит Х т цемента в день. По договору он должен ежедневно поставлять строительной фирме не менее 20 т цемента. Производственные мощности завода таковы, что выпуск цемента не может превышать 90 т в день.
Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид:
К=-х3+98х2+200х. Удельные затраты составят К/х=-х2+98х+200. |
задача сводится к отысканию наибольшего и наименьшего значения функции
Y= -х2+98х+200.
|
| 6. На изготовление открытого бака заданного объема 32 м3 в форме прямоугольного параллелепипеда, в основании которого квадрат, хотят затратить наименьшее количество металла. Какова должна быть ширина и высота бака?
| Пусть х – сторона основания бака, h – высота. Выразить h через x и V. Найти S общей поверхности бака, S = S(x). Задача сводится к отысканию наименьшего значения функции S(x). |
5 ЭТАП. Итог урока
Пока группа экспертов проверяет работы учащихся по подготовленным шаблонам, учащиеся подводят итоги, отвечая на вопросы учителя:
Назовите имена учёных, внёсших вклад в создание и развитие дифференциального исчисления.
С какими новыми понятиями вы познакомились в процессе изучения темы?
Задачи какого рода решаются с помощью производной?
Назовите сферы приложения производной.
Учитель предлагает учащимся вспомнить, какие цели ставились в начале уроке, и обсудить, все ли удалось выполнить.
В это время эксперты завершают работу по проверке заключительного теста. Полученные результаты доводятся до сведения учащихся, которые фиксируют их в оценочных листах.
Подсчитанные учащимися баллы вносятся в оценочные листы в графу «самооценка». Учитель может выяснить у учащихся результаты самостоятельного оценивания своего труда. По числу поднятых рук легко подсчитать количество оценок каждого вида, и присутствующим будут понятны предварительные итоги урока и степень готовности класса к контрольной работе.
1. Самооценка труда учащихся.
Заполни таблицу:
Фамилия, имя_______________________
Бланк выставления баллов
| № п/п | Этапы урока | Количество баллов |
| 1 | Я знаю таблицу производных и правила дифференцирования
|
|
| 2 | Работа у доски
|
|
| 3 | Работа по карточкам с практическими заданиями
|
|
| 4 | Устная работа с классом
|
|
| 5 | Работа по группам с дополнительным материалом
|
|
| 6 | Решение задачи повышенного уровня
|
|
2. Оценка труда товарищей:
Кто, по-вашему мнению, внес наибольший вклад;
Кому, над чем следовало бы еще поработать.
Ребята, давайте оценим нашу работу на уроке.
В заключении урока я хочу вам прочитать стихотворение:
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей”.
Так сказал американский математик Морис Клайн.
Спасибо за работу!
Получите свидетельство
Вход
Применение производной в различных областях науки (0.55 MB)
1
2733
330
Нравится
0
