Пояснительная записка
Данная программа по математике составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования, примерной программы среднего (полного) общего образования по математике (профильный уровень) и программ по алгебре и началам анализа Мордковича А.Г., по геометрии Атанасяна Л.С.
Курс «Математика» представлен двумя отдельными самостоятельными модулями: алгебра и начала анализа, геометрия.
Программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. В программу модуля «Алгебра и начала анализа» включена тема «Элементы статистики и теории вероятностей».
Цели
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
Задачи:
• систематизировать сведения о числах; формировать представления о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствовать технику вычислений;
• развить и совершенствовать технику алгебраических преобразований, решения уравнений, неравенств, систем;
• систематизировать и расширять сведения о функциях, совершенствовать графические умения; знакомиться с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
• расширять системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развить представления о геометрических измерениях;
• развить представления о вероятностно-статистических закономерностях в окружающем мире;
• совершенствовать математическое развитие до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
• формировать способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Учебные модули «Алгебра и начала анализа» и «Геометрия» опираются на вычислительные и графические умения и навыки учащихся, полученные на уроках математики с 5 по 9 класс; являются базой для предметов естественно – математического цикла, где необходимы вычислительные операции, преобразования выражений, в частности формул.
Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану 2004 года для образовательных учреждений Российской Федерации на изучение математики на ступени среднего (полного) общего образования отводится не менее 408 ч из расчета 6 ч в неделю с 10 по 11 класс.
На модуль «Алгебра и начала анализа»: в 10 классе - 136 часов (4 часа в неделю); на модуль «Геометрия»: в 10 классе 68 часов (2 часа в неделю).
На модуль «Алгебра и начала анализа»: в 11 классе - 136 часов (4 часа в неделю); на модуль «Геометрия»: в 11 классе 68 часов (2 часа в неделю).
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все выпускники, изучавшие курс математики по профильному уровню, и достижение которых является обязательным условием положительной аттестации ученика за курс средней (полной) школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние две компоненты представлены отдельно по каждому из разделов, содержания.
Требования к уровню подготовки обучающихся.
В результате изучения математики на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностных характер различных процессов и закономерностей окружающего мира;
Числовые и буквенные выражения
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа
уметь
находить сумму бесконечно убывающей геометрической прогрессии;
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы;
исследовать функции и строить их графики с помощью производной;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа;
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять вероятности событий на основе подсчета числа исходов (простейшие случаи);
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Геометрия
уметь
соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
строить сечения многогранников и изображать сечения тел вращения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Учебно – тематический план
Модуль «Алгебра и начала анализа» 10 класс
(4 часа в неделю, всего 136 ч.)
| № п/п |
Тема | Количество часов | В том числе контрольные работы |
| 1 | Числовые функции | 5 |
|
| 1.1 | Определение числовой функции и способы ее задания | 2 |
|
| 1.2 | Свойства функций | 2 |
|
| 1.3 | Обратная функция | 1 |
|
| 2 | Тригонометрические функции | 23 |
|
| 2.1 | Числовая окружность | 2 |
|
| 2.2 | Числовая окружность на координатной плоскости | 2 |
|
|
| Контрольная работа № 1по теме «Числовые функции. Числовая окружность» | 1 | 1 |
| 2.3 | Синус и косинус числа. Тангенс и котангенс числа. Радианная мера угла. Синус, косинус, тангенс, котангенс произвольного угла. | 2 |
|
| 2.4 | Тригонометрические функции числового аргумента | 2 |
|
| 2.5 | Тригонометрические функции углового аргумента. Основные тригонометрические тождества | 1 |
|
| 2.6 | Формулы приведения | 2 |
|
|
| Контрольная работа № 2 по теме «Определение тригонометрических функций» | 1 | 1 |
| 2.7 | Функция у = sin x. Ее свойства и график, периодичность, основной период. Обратная функция, ее график | 2 |
|
| 2.8 | Функция у = соs x. Ее свойства и график, периодичность, основной период. Обратная функция, ее график | 2 |
|
| 2.9 | Периодичность функций у = sin x и у = соs x | 1 |
|
| 2.10 | Преобразования графиков тригонометрических функций | 2 |
|
| 2.11 | Функции у = tg x, y = ctg x. Их свойства и графики, периодичность, основной период | 2 |
|
|
| Контрольная работа № 3по теме « Свойства и графики тригонометрических функций» | 1 | 1 |
| 3 | Тригонометрические уравнения | 9 |
|
| 3.1 | Арккосинус. Решение уравнений соs t = a, tg x = a, сtg x = a и неравенств. Арксинус, арккосинус, арктангенс числа. | 2 |
|
| 3.2 | Арксинус. Решение уравнений sin t = a. | 2 |
|
| 3.3 | Арктангенс и арккотангенс. Решение уравнений tg x = a, сtg x = a. | 1 |
|
| 3.4 | Решение тригонометрических уравнений: - сведение к квадратному; - разложение на множители; - введение новой переменной; - сведение к однородному уравнению. |
3 |
|
|
| Контрольная работа № 4 по теме «Тригонометрические уравнения» | 1 | 1 |
| 4 | Преобразование тригонометрических выражений | 11 |
|
| 4.1 | Синус и косинус суммы аргументов и разности аргументов | 2 |
|
| 4.2 | Тангенс суммы и разности аргументов | 1 |
|
| 4.3 | Формулы двойного аргумента | 2 |
|
| 4.4 | Преобразование сумм тригонометрических функций в произведение | 3 |
|
| 4.5 | Преобразование произведений тригонометрических функций в суммы | 2 |
|
|
| Контрольная работа № 5по теме «Формулы тригонометрии» | 1 | 1 |
| 5 | Производная | 27 |
|
| 5.1 | Числовые последовательности и их свойства. Предел последовательности. | 1 |
|
| 5.2 | Сумма бесконечной геометрической прогрессии | 1 |
|
| 5.3 | Предел функции. Приращение аргумента, приращение функции. Понятие о непрерывности функции. | 3 |
|
| 5.4 | Определение производной функции, физический и геометриический смысл производной. Алгоритм отыскания производной. |
3 |
|
| 5.5 | Вычисление производных: - производные основных элементарных функций; формулы дифференцирования для функций у = С, у = kx + m, y = 1/x, y = x2, y = x, y = sin x, y = cos x, у = tg x, у = с tg x, у = хn; - правила дифференцирования (сумма, произведение, частное); - дифференцирование функции у = f(kx + m); - производные обратной функции и композиции данной функции с линейной. |
3 |
|
|
| Контрольная работа № 6 по теме «Числовые последовательности. Правила и формулы отыскания производных» | 1 | 1 |
| 5.6 | Уравнение касательной к графику функции | 2 |
|
|
| Применение производной для исследования функций на монотонность и экстремумы. |
3 |
|
| 5.7 | Построение графиков функций, графики дробно-линейных функций. | 3 |
|
|
| Контрольная работа № 7по теме «Применение производной к исследованию функций» | 1 | 1 |
| 5.8 | Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке. |
2 |
|
| 5.9 | Задачи на отыскание наибольших и наименьших значений величин. | 3 |
|
|
| Контрольная работа № 8по теме «Применение производной для отыскания наибольшего и наименьшего значений на промежутке» | 1 | 1 |
| 6 | Повторение курса | 7 |
|
|
| Тригонометрические функции. | 1 |
|
|
| Тригонометрические уравнения. | 1 |
|
|
| Преобразования тригонометрических выражений. | 1 |
|
|
| Вычисление производных. | 1 |
|
|
| Применение производной для исследования функций. | 1 |
|
|
| Применение производной для отыскания наибольшего и наименьшего значений функции на промежутке. | 1 |
|
|
| Задачи на отыскание наибольших и наименьших значений величин. | 1 |
|
|
| Итого | 82 |
|
Учебно – тематический план
Модуль «Алгебра и начала анализа» 11 класс
(I, II – четверти 3 часа в неделю, III, IV четверти – 2 часа в неделю, всего 82 ч.)
| № п/п |
Тема | Количество часов | В том числе контрольные работы |
| 1 | Степени и корни. Степенные функции. | 15 |
|
| 1.1 | Понятие корня n-й степени из действительного числа | 2 |
|
| 1.2 | Функции у = 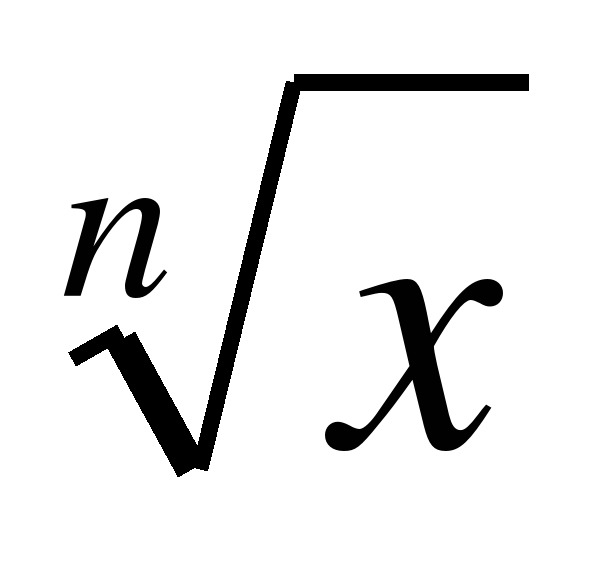 , их свойства и графики , их свойства и графики | 2 |
|
| 1.3 | Свойства корня n-ой степени. | 2 |
|
| 1.4 | Преобразование выражений, содержащих радикалы. | 3 |
|
|
| Контрольная работа № 1 по теме «Корень n-ой степени» | 1 | 1 |
|
| Обобщение понятия о показателе степени: - степень с рациональным показателем и ее свойства; - понятие о степени с действительным показателем. Свойства степени с действительным показателем. | 2 |
|
|
| Степенные функции, их свойства и графики | 3 |
|
| 2 | Показательная и логарифмическая функции | 24 |
|
| 2.1 | Показательная функция (экспонента), ее свойства и график | 3 |
|
| 2.2 | Показательные уравнения, основные виды и методы их решения. Показательные неравенства, основные виды и методы их решения | 3 |
|
|
| Контрольная работа №2 по теме «Степенные и показательная функции. Показательные уравнения и неравенства» | 1 | 1 |
| 2.3 | Понятие логарифма. | 1 |
|
| 2.4 | Логарифмическая функция, ее свойства и график | 2 |
|
| 2.5 | Свойства логарифмов | 2 |
|
| 2.6 | Логарифмические уравнения | 3 |
|
|
| Контрольная работа № 3 по теме «Свойства логарифмов. Логарифмические уравнения. Логарифмическая функция». | 1 | 1 |
| 2.7 | Логарифмические неравенства | 3 |
|
| 2.8 | Переход к новому основанию логарифма | 2 |
|
| 2.9 | Дифференцирование показательной и логарифмической функций | 2 |
|
|
| Контрольная работа № 4 по теме «Логарифмические неравенства. Дифференцирование показательной и логарифмической функции» | 1 | 1 |
| 3 | Первообразная и интеграл | 7 |
|
| 3.1 | Первообразная и неопределенный интеграл. | 3 |
|
| 3.2 | Определенный интеграл: - определенный интеграл, его вычисление и свойства; - вычисление площади криволинейной трапеции с помощью определенного интеграла. Формула Ньютона-Лейбница |
3
|
|
|
| Контрольная работа № 5 по теме «Первообразная и интеграл» | 1 | 1 |
| 4 | Элементы математической статистики, комбинаторики и теории вероятностей | 11 |
|
| 4.1 | Статистическая обработка данных | 2 |
|
| 4.2 | Простейшие вероятностные задачи | 2 |
|
| 4.3 | Сочетания и размещения | 2 |
|
| 4.4 | Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. |
2 |
|
| 4.5 | Элементарные, сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статическая частота наступления события |
2 |
|
|
| Контрольная работа №6 по теме «Элементы комбинаторики, статистики и теории вероятностей» | 1 | 1 |
| 5 | Уравнения и неравенства. Системы уравнений и неравенств | 17 |
|
| 5.1 | Равносильность уравнений, неравенств, систем.
| 2 |
|
| 5.2 | Общие методы решения уравнений. | 3 |
|
| 5.3 | Решение неравенств с одной переменной. Общие методы решения неравенств. Метод интервалов. Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем. | 3 |
|
| 5.4 | Уравнения и неравенства с двумя переменными
| 1 |
|
| 5.5 | Системы уравнений Основные приемы решения систем уравнений: - подстановка; - алгебраическое сложение; - введение новых переменных. |
3 |
|
| 5.6 | Уравнения и неравенства с параметрами | 3 |
|
|
| Контрольная работа №7 по теме «Уравнения и неравенства. Системы уравнений и неравенств» | 2 | 2 |
| 6 | Повторение курса | 6 |
|
| 6.1 | Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Обратная функция. Область определения и область значений обратной функции. График обратной функции. | 1 |
|
| 6.2 | Преобразования графиков. Чтение графиков | 1 |
|
| 6.3 | Тригонометрические функции. Тригонометрические уравнения | 1 |
|
| 6.4 | Преобразования тригонометрических выражений | 1 |
|
| 6.5 | Применение производной | 1 |
|
| 6.6 | Решение текстовых задач | 1 |
|
|
| Подготовка к ЕГЭ | 2 |
|
|
| Итого | 82 |
|
Учебно-тематический план
Модуль «Геометрия» 10 класс
(I, II – четверти 1 час в неделю, III, IV четверти – 2 часа в неделю, всего 54 ч.)
| № п/п |
Тема | Количество часов | В том числе контрольные работы |
| 1 | Введение (аксиомы стереометрии и их следствия) | 4 |
|
| 1.1 | Предмет стереометрии. Аксиомы стереометрии. Основные понятия стереометрии (точка, прямая, плоскость, пространство) | 1 |
|
| 1.2 | Некоторые следствия из аксиом | 1 |
|
| 1.3 | Решение задач на применение аксиом стереометрии и их следствий. | 2 |
|
| 2 | Параллельность прямых и плоскостей | 15 |
|
| 2.1 | Параллельность прямых, прямой и плоскости | 4 |
|
| 2.1.1 | Параллельные прямые в пространстве. Параллельность трех прямых | 1 |
|
| 2.1.2 | Параллельность прямой и плоскости | 1 |
|
| 2.1.3 | Повторение теории, решение задач на параллельность прямой и плоскости. | 2 |
|
| 2.2 | Взаимное расположение прямых в пространстве. Угол между двумя прямыми | 5 |
|
| 2.2.1 | Пересекающиеся и скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой | 1 |
|
| 2.2.2 | Углы с сонаправленными сторонами. Угол между прямыми в пространстве | 1 |
|
| 2.2.3 | Повторение теории, решение задач по теме | 1 |
|
|
| Контрольная работа № 1 по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости» | 1 | 1 |
| 2.3 | Параллельность плоскостей | 2 |
|
| 2.3.1 | Параллельные плоскости. Признак параллельности двух плоскостей. Свойства параллельных плоскостей | 2 |
|
| 2.4 | Тетраэдр и параллелепипед | 5 |
|
| 2.4.1 | Тетраэдр. Параллелепипед. Свойства граней и диагоналей параллелепипеда. | 1 |
|
| 2.3.2 | Задачи на построение сечений куба, параллелепипеда. | 1 |
|
| 2.3.3 | Повторение теории, решение задач по теме | 1 |
|
|
| Контрольная работа № 2 по теме «Параллельность прямых и плоскостей» | 1 | 1 |
|
| Зачет №1 по теме «Параллельность прямых и плоскостей» | 1 |
|
| 3 | Перпендикулярность прямых и плоскостей. | 17 |
|
| 3.1 | Перпендикулярность прямой и плоскости | 4 |
|
| 3.1.1 | Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости | 1 |
|
| 3.1.2 | Признак перпендикулярности прямой и плоскости | 1 |
|
| 3.1.3 | Теорема о прямой, перпендикулярной к плоскости | 1 |
|
| 3.1.4 | Решение задач на перпендикулярности прямой и плоскости | 1 |
|
| 3.2 | Перпендикуляр и наклонные. Угол между прямой и плоскостью | 6 |
|
| 3.2.1 | Расстояние от точки до плоскости, расстояние от прямой до плоскости, расстояние между параллельными плоскостями, расстояние между скрещивающимися прямыми. Теорема о трех перпендикулярах | 1 |
|
| 3.2.2 | Угол между прямой и плоскостью | 1 |
|
| 3.2.3 | Повторение теории, решение задач на применение теоремы о трех перпендикулярах, на угол между прямой и плоскостью | 4 |
|
| 3.3 | Двугранный угол. Перпендикулярность плоскостей | 7 |
|
| 3.3.1 | Двугранный угол, линейный угол двугранного угла. Многогранные углы. Признак перпендикулярности двух плоскостей. | 2 |
|
| 3.3.2 | Прямоугольный параллелепипед | 2 |
|
| 3.3.3 | Повторение теории, решение задач по всей теме | 1 |
|
|
| Контрольная работа № 3 по теме «Перпендикулярность прямых и плоскостей» | 1 | 1 |
|
| Зачет №2 по теме «Перпендикулярность прямых и плоскостей» | 1 |
|
| 4 | Многогранники | 12 |
|
| 4.1 | Понятие многогранника. Призма | 3 |
|
| 4.1.1 | Понятие многогранника. Вершины, ребра, грани многогранника. Развертка. Призма, ее основания, боковые ребра, высота, боковая поверхность, площадь поверхности призмы | 3 |
|
| 4.2 | Пирамида | 4 |
|
| 4.2.1 | Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Площадь поверхности пирамиды | 4 |
|
| 4.3 | Правильные многогранники | 5 |
|
| 4.3.1 | Симметрии в пространстве. Понятие правильного многогранника (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр). Элементы симметрии правильных многогранников. Теорема Эйлера*. | 2 |
|
| 4.3.2 | Решение задач по теме «Многогранники» | 1 |
|
|
| Контрольная работа №4 по теме «Многогранники» | 1 | 1 |
|
| Зачет №3 по теме «Многогранники. Площадь поверхности призмы и пирамиды» |
|
|
| 5 | Повторение курса. | 5 |
|
|
| Аксиомы стереометрии и их следствия. | 1 |
|
|
| Параллельность прямых и плоскостей. | 1 |
|
|
| Перпендикулярность прямых и плоскостей. | 1 |
|
|
| Многогранники. | 1 |
|
|
| Заключительный урок-беседа по курсу геометрии 10 класса | 1 |
|
|
| Итого | 54 | 4 |
Учебно-тематический план
Модуль «Геометрия» 11 класс
(I, II – четверти 1 час в неделю, III, IV четверти – 2 часа в неделю, всего 54 ч.)
| № п/п |
Тема | Количество часов | В том числе контрольные работы |
| 1 | Векторы в пространстве | 5 |
|
| 1.1 | Понятие вектора в пространстве | 1 |
|
| 1.1.1 | Понятие вектора. Модуль вектора. Равенство векторов | 1 |
|
| 1.2 | Сложение и вычитание векторов. Умножение вектора на число | 2 |
|
| 1.2.1 | Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. Угол между векторамми | 2 |
|
| 1.3 | Компланарные векторы | 2 |
|
| 1.3.1 | Компланарные векторы. Правило параллелепипеда. Разложение вектора по трем некомпланарным векторам | 2 |
|
| 2 | Метод координат в пространстве | 15 |
|
| 2.1 | Координаты точки и координаты вектора | 6 |
|
| 2.1.1 | Прямоугольная система координат в пространстве | 1 |
|
| 2.1.2 | Координаты вектора. | 1 | |
| 2.1.3 | Связь между координатами векторов и координатами точек | 1 |
|
| 2.1.4 | Простейшие задачи в координатах. Формула расстояния между двумя точками | 3 |
|
|
| Контрольная работа № 1 по теме «Простейшие задачи в координатах» | 1 | 1 |
| 2.2 | Скалярное произведение векторов | 5 |
|
| 2.2.1 | Угол между векторами. Скалярное произведение векторов. Коллинеарные векторы. Разложение векторов по двум неколлинеарным векторам. | 2 |
|
| 2.2.2 | Вычисление углов между прямыми и плоскостями | 1 |
|
| 2.2.3 | Уравнение плоскости. Расстояние от точки до плоскости. | 2 |
|
| 2.3 | Движения | 4 |
|
| 2.3.1 | Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос | 2 |
|
|
| Контрольная работа № 2 по теме «Скалярное произведение векторов в пространстве. Движение» | 1 | 1 |
|
| Зачет №1 по теме «Метод координат в пространстве» | 1 |
|
| 3 | Цилиндр, конус и шар | 10 |
|
| 3.1 | Цилиндр | 3 |
|
| 3.1.1 | Понятие цилиндра. Основание, высота, боковая поверхность, образующая, развертка цилиндра. Площадь поверхности цилиндра. Осевые сечения и сечения, параллельные основанию. | 3 |
|
| 3.2 | Конус | 3 |
|
| 3.2.1 | Понятие конуса. Основание, высота, боковая поверхность, образующая, развертка конуса. Площадь поверхности конуса. Усеченный конус. Осевые сечения и сечения, параллельные основанию | 3 |
|
| 3.3 | Сфера | 4 |
|
| 3.3.1 | Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости. Сечения сферы и шара. Касательная плоскость к сфере. Площадь сферы | 4 |
|
|
| Контрольная работа № 3 по теме «Тела вращения» | 1 | 1 |
| 4 | Объемы тел | 16 |
|
| 4.1 | Объем прямоугольного параллелепипеда | 3 |
|
| 4.1.1 | Понятие объема. Отношение объемов подобных тел. Формулы объема куба, прямоугольного параллелепипеда | 3 |
|
| 4.2 | Объем прямой призмы. Объем цилиндра | 2 |
|
| 4.2.1 | Теорема об объеме прямой призмы и цилиндра | 2 |
|
| 4.3 | Объем наклонной призмы, пирамиды и конуса | 4 |
|
| 4.3.1 | Вычисление объемов тел с помощью определенного интеграла. Объем наклонной призмы. Объем пирамиды. Объем конуса | 4 |
|
| 4.4 | Объем шара и площадь сферы | 7 |
|
| 4.4.1 | Объем шара. Объем шарового сегмента, шарового слоя и шарового сектора. Площадь сферы | 5 |
|
|
| Контрольная работа №4 по теме «Объем шара и его частей», «Площадь сферы» | 1 | 1 |
|
| Зачет по теме «Объемы тел» | 1 |
|
| 5 | Заключительное повторение курса геометрии, подготовка к итоговой аттестации | 8 |
|
| 5.1 | Аксиомы стереометрии. Параллельность прямых, прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей. | 1 |
|
| 5.2 | Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. | 1 |
|
| 5.3 | Двугранный угол. Перпендикулярность плоскостей. | 1 |
|
| 5.4 | Многогранники: параллелепипед, призма, пирамида, площади их поверхностей. | 1 |
|
| 5.5 | Векторы в пространстве. Действия над векторами. Скалярное произведение векторов. | 1 |
|
| 5.6 | Цилиндр, конус и шар, площади их поверхностей. | 1 |
|
| 5.7 | Объемы тел. | 2 |
|
|
| Итого | 54 | 3 |
Содержание учебного предмета
Модуль «Алгебра и начала анализа» 10 класс
I. Действительные числа. (13 ч.)
Натуральные и целые числа. Делимость натуральных чисел. Признаки делимости. Простые и составные числа. Деление с остатком. Наибольший общий делитель и наименьшее общее кратное. Основная теорема арифметики. Рациональные числа. Иррациональные числа. Множество действительных чисел. Модуль действительного числа. Свойства модулей. Геометрический смысл модуля. Решение уравнений и неравенств с модулем. Метод математической индукции. Принцип математической индукции.
В результате изучения темы учащийся должен
знать/понимать:
- понятия натурального, целого, рационального, иррационального, действительного числа;
- понятия простого и составного числа;
- свойства делимости натуральных чисел;
- признаки делимости натуральных чисел;
- понятие модуля действительного числа;
- свойства модуля;
- геометрический смысл модуля;
- метод математической индукции;
уметь:
- выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств;
- делить с остатком;
- решать уравнения и неравенства с модулем;
- решать и доказывать, используя свойства и признаки натуральных чисел;
- доказывать, используя метод и принцип математической индукции.
использовать в практической деятельности:
для практических расчетов по формулам, включая формулы, содержащие степени
приобретать опыт:
- конструирования новых моделей для возникших ситуаций.
Основные понятия:
Делимое, делитель, кратное. Простые и составные числа. Взаимно-простые числа. Наибольший общий делитель и наименьшее общее кратное. Модуль действительного числа.
Контрольная работа № 1 по теме «Действительные числа».
II. Числовые функции. (9 ч)
Определение числовой функции и способы ее задания. Свойства числовой функции: область определения функции, область значений, монотонность, ограниченность, наименьшее и наибольшее значения на промежутке области определения, четность и нечетность. Периодические функции. График числовой функции. Обратная функция. График обратной функции.
В результате изучения темы учащийся должен
знать/понимать:
- определение числовой функции и способы ее задания;
- график числовой функции;
- основные свойства числовой функции;
- определение обратной функции;
уметь:
- вычислять значения функции по известному значению аргумента;
- строить графики изученных функций, выполнять преобразования графиков;
- описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику наибольшее и наименьшее значения;
- находить обратную функцию и строить ее график.
использовать в практической деятельности:
- для описания и исследования с помощью числовых функций реальных зависимостей (природных, социальных и т.д.), представления их графически;
приобретать опыт:
- конструирования новых моделей для возникших ситуаций.
Основные понятия:
числовая функция; график числовой функции; кусочная функция; возрастающая и убывающая функции; ограниченная сверху, ограниченная снизу, ограниченная функции; наименьшее и наибольшее значение функции на множестве; четная и нечетная функции; обратная функция.
Контрольная работа № 2 по теме «Числовые функции».
III. Тригонометрические функции. (25 ч)
Введение (длина дуги окружности). Числовая окружность. Числовая окружность на координатной плоскости. Синус и косинус числа. Тангенс и котангенс числа. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента. Радианная мера угла. Основные тригонометрические тождества. Формулы приведения. Функция у = sin x. Ее свойства и график, периодичность, основной период. Обратная функция, ее график. Функция у = соs x. Ее свойства и график, периодичность, основной период. Обратная функция, ее график. Как построить график функции у = mf(x), если известен график функции у = f(x). Как построить график функции у = f(kx), если известен график функции у = f(x). График гармонического колебания. Функции у = tg x, y = ctg x. Их свойства и графики, периодичность, основной период.
В результате изучения темы учащийся должен
знать/понимать:
- определения синуса, косинуса, тангенса, котангенса произвольного угла;
- основные тригонометрические тождества;
- формулы приведения;
- свойства тригонометрических функций их графики;
уметь:
- вычислять значения тригонометрических функций по известному значению одной из них;
- строить графики тригонометрических функций, выполнять преобразования графиков;
- находить основной период тригонометрических функций;
- проводить преобразования тригонометрических выражений, используя основные тригонометрические тождества;
использовать в практической деятельности:
- для описания и исследования с помощью тригонометрических функций реальных зависимостей (природных, социальных и т.д.), представления их графически;
приобретать опыт:
- конструирования новых моделей для возникших ситуаций.
Основные понятия:
тригонометрические функции, синусоида, тангенсоида, периодичность функции, период функции, периодичность, период, основной период.
Контрольная работа № 3 по теме «Тригонометрические функции».
IV. Тригонометрические уравнения. ( 9 ч )
Первые представления о решении простейших тригонометрических уравнений соs x = a, sin x = a, tg x = a, сtg x = a и неравенств. Решение тригонометрических уравнений: сведение к квадратному; разложение на множители; введение новой переменной; сведение к однородному уравнению.
В результате изучения темы учащийся должен
знать/понимать:
- понятия арксинуса, арккосинуса, арктангенса;
- формулы корней простейших тригонометрических уравнений;
- алгоритмы решений тригонометрических уравнений;
уметь:
- решать простейшие тригонометрические уравнения ;
- решать более сложные уравнения приведением их к виду, содержащему одну функцию одного аргумента с последующей заменой переменной;
- решать тригонометрические уравнения с применением графических представлений и свойств функции;
использовать в практической деятельности:
- для построения и исследования простейших математических моделей;
приобретать опыт:
- планирования и осуществления алгоритмической деятельности.
Основные понятия:
тригонометрические уравнения, арксинус числа, арккосинус числа, арктангенс числа, арккотангенс числа, простейшее тригонометрическое уравнение, однородное тригонометрическое уравнение первой и второй степени.
Контрольная работа № 4 по теме «Тригонометрические уравнения»
V. Преобразование тригонометрических выражений. (20 ч )
Синус и косинус суммы аргументов. Синус и косинус разности аргументов. Тангенс суммы и разности аргументов. Формулы приведения. Формулы двойного аргумента. Формулы понижения степени. Формулы половинного угла. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в сумму. Преобразования простейших тригонометрических выражений. Преобразование выражения A∙sin x + B ∙cos x к виду С∙sin(x+t). Методы решения тригонометрических уравнений.
В результате изучения темы учащийся должен
знать/понимать:
- формулы тригонометрии: синус, косинус и тангенс суммы и разности двух аргументов; синус и косинус двойного аргумента;
- формулы приведения;
- формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму;
уметь:
- проводить преобразования тригонометрических выражений с использованием вышеуказанных формул;
использовать в практической деятельности:
- для исследования изучаемых моделей с использованием аппарата формул тригонометрии;
приобретать опыт:
- конструирования новых алгоритмов.
Основные понятия:
тригонометрические функции суммы и разности двух углов, тригонометрические функции двойного аргумента, формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму.
Контрольная работа № 5 по теме «Преобразование тригонометрических выражений»
VI. Комплексные числа (9 ч.)
Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость. Тригонометрическая форма записи комплексного числа. Комплексные числа и квадратные уравнения. Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа.
В результате изучения темы учащийся должен
знать/понимать:
- понятие комплексного числа, свойства комплексных чисел, действия с комплексными числами;
- тригонометрическая форма записи комплексного числа;
- геометрическую интерпретацию комплексных чисел;
уметь:
- выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
использовать в практической деятельности:
- для практических расчетов по формулам, включая формулы, содержащие степени;
приобретать опыт:
- конструирования новых алгоритмов.
Основные понятия:
понятие комплексного числа, свойства комплексных чисел, тригонометрическая форма записи комплексного числа; геометрическую интерпретацию комплексных чисел.
Контрольная работа № 6 по теме «Комплексные числа»
V. Производная. ( 28 ч)
Числовые последовательности. Понятие о пределе числовой последовательности. Предел функции. Приращение аргумента, приращение функции. Определение производной: задачи, приводящие к понятию производной; определение производной, ее геометрический и физический смысл; алгоритм отыскания производной. Вычисление производных: производные основных элементарных функций; формулы дифференцирования для функций у = С, у = kx + m, y = 1/x, y = x2, y = x, y = sin x, y = cos x, у = tg x, у = сtg x, у = хn; правила дифференцирования (сумма, произведение, частное); дифференцирование функции у = f(kx + m); производные обратной функции и композиции данной функции с линейной. Уравнение касательной к графику функции. Применение производной к исследованию функции: исследование функции на монотонность; отыскание точек экстремума; построение графиков функций, графики дробно-линейных функций. Отыскание наибольших и наименьших значений функций: отыскание наибольшего и наименьшего значений для непрерывной функции на промежутке; задачи на отыскание наибольших и наименьших значений величин.
В результате изучения темы учащийся должен
знать/понимать:
- понятие производной;
- геометрический и механический смысл производной;
- правила и формулы дифференцирования;
- алгоритмы отыскания производной, составления уравнения касательной к графику функции, исследования функции на монотонность и экстремумы, отыскания наибольшего и наименьшего значений непрерывной функции на промежутке;
уметь:
- вычислять производные, применяя правила вычисления производных, используя справочные материалы;
- исследовать функции и строить их графики с помощью производной;
- решать задачи с применением уравнения касательной к графику функции;
- решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
использовать в практической деятельности:
- нахождение скорости при неравномерном движении;
- выполнение приближенных вычислений с помощью производной;
приобретать опыт:
- моделирования практических ситуаций через конструирование математических моделей.
Основные понятия:
приращение аргумента, приращение функции, производная, касательная к графику функции, точка экстремума (максимума, минимума) функции, стационарная точка.
Контрольная работа № 7 по теме «Числовые последовательности. Правила и формулы отыскания производных»
Контрольная работа № 8 по теме «Применение производной для отыскания наибольшего и наименьшего значений на промежутке».
VI. Комбинаторика и вероятность. (8 ч)
Правила умножения. Комбинаторные задачи. Перестановка и факториалы. Выбор нескольких элементов. Сочетания и размещения. Биномиальные коэффициенты. Случайные события и их вероятности.
В результате изучения темы учащийся должен
знать/понимать:
- классическую схему вероятности, классическое определение вероятности;
- правило умножения.
- алгоритм нахождения вероятности случайного события.
- алгоритмы отыскания производной, составления уравнения касательной к графику функции, исследования функции на монотонность и экстремумы, отыскания наибольшего и наименьшего значений непрерывной функции на промежутке;
-универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
- вероятностный характер различных процессов окружающего мира;
уметь:
- решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
- вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать в практической деятельности:
- анализ реальных числовых данных, представленных в виде диаграмм, графиков.
- анализ информации статического характера.
Основные понятия:
число перестановок, число сочетаний, число размещений, биномиальные коэффициенты, сложные события, несовместные события, вероятность события.
Контрольная работа № 9 по теме: «Комбинаторика и вероятность».
VII. Итоговое повторение. (14 ч)
Действительные числа и операции над ними. Числовые функции. Тригонометрические функции. Тригонометрические уравнения. Преобразования тригонометрических выражений. Комплексные числа и арифметические операции над ними. Вычисление производных. Применение производной для исследования функций. Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке. Задачи на отыскание наибольших и наименьших значений величин. Комбинаторика и вероятность.
Итоговая контрольная работа.
Содержание учебного предмета
Модуль «Алгебра и начала анализа» 11 класс
1. Степени и корни. Степенные функции. ( 15 ч )
Понятие корня n-й степени из действительного числа. Функции у = 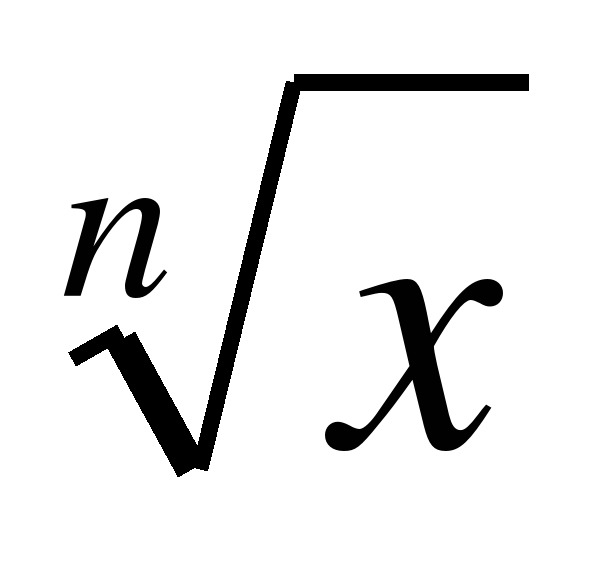 , их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени: степень с рациональным показателем и ее свойства; понятие степени с действительным показателем. Степенная функция с натуральным показателем, ее свойства и график (производная и первообразная степенной функции с рациональным показателем).
, их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени: степень с рациональным показателем и ее свойства; понятие степени с действительным показателем. Степенная функция с натуральным показателем, ее свойства и график (производная и первообразная степенной функции с рациональным показателем).
В результате изучения темы учащийся должен
знать/понимать:
- свойства корня n-й степени;
- понятие степени с рациональным показателем;
- свойства степенной функции;
уметь:
- находить значение корня n-й степени, используя при необходимости вычислительные устройства, пользоваться оценкой и прикидкой при практических расчетах;
- проводить преобразования выражений, содержащих корень n-й степени и операции возведения в степень;
- строить график степенной функции с натуральным показателем;
использовать в практической деятельности:
- умения рассчитывать по формулам, содержащим корень n-й степени, при необходимости преобразуя и используя справочные материалы и вычислительные устройства;
приобретать опыт:
- вычислений при осуществлении алгоритмической деятельности.
Основные понятия:
показатель степени, корень n-й степени, радикал, иррациональное выражение, степень с рациональным показателем, степенная функция.
Контрольная работа № 1 по теме «Корень n-ой степени».
2. Показательная и логарифмическая функции. ( 24 ч )
Показательная функция (экспонента), ее свойства и график. Показательные уравнения, основные виды и методы их решения. Показательные неравенства, основные виды и методы их решения. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени, переход к новому основанию. Десятичный и натуральный логарифмы, число е. Преобразования логарифмических выражений. Логарифмическая функция, ее свойства и график. Логарифмические уравнения. Логарифмические неравенства. Производная показательной и логарифмической функций. Решение систем показательных и логарифмических уравнений и неравенств.
В результате изучения темы учащийся должен
знать/понимать:
- определения логарифма и его свойства;
- свойства показательной и логарифмической функций;
- алгоритм решения логарифмических и показательных уравнений и неравенств;
уметь:
- находить значение логарифма, выражений, содержащих логарифм и показательных выражений;
- проводить преобразования показательных выражений и выражений, содержащих логарифм;
- решать показательные и логарифмические уравнения и неравенства;
- решать системы показательных и логарифмических уравнений и неравенств;
- решать уравнения, неравенства и системы с применением графических представлений, свойств показательной и логарифмической функций;
- выполнять преобразования графиков показательной и логарифмической функций;
использовать в практической деятельности:
- умение строить, исследовать и решать простейшие математические модели.
приобретать опыт:
- планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов.
Основные понятия:
показательная функция, показательное уравнение, показательное неравенство, логарифм числа, основание логарифма, десятичный логарифм, натуральный логарифм, логарифмическая функция, логарифмическое уравнение, логарифмическое неравенство, экспонента, число е.
Контрольная работа № 2 по теме «Степенные и показательная функции. Показательные уравнения и неравенства».
Контрольная работа № 3 по теме «Свойства логарифмов. Логарифмические уравнения. Логарифмическая функция».
Контрольная работа № 4 по теме «Логарифмические неравенства. Дифференцирование показательной и логарифмической функции».
3. Первообразная и интеграл ( 9 ч )
Первообразная и неопределенный интеграл. Определенный интеграл: определенный интеграл, его вычисление и свойства; вычисление площади криволинейной трапеции с помощью определенного интеграла. Формула Ньютона-Лейбница.
В результате изучения темы учащийся должен
знать/понимать:
- понятие первообразной;
- интегрирование как операцию, обратную дифференцированию;
- алгоритм нахождения первообразной и вычисления определенного интеграла;
уметь:
- вычислять первообразные элементарных функций, применяя правила вычисления первообразных;
- вычислять площадь криволинейной трапеции;
использовать в практической деятельности:
- для решения геометрических, физических, экономических и других прикладных задач с применением аппарата математического анализа;
приобретать опыт:
- построения и исследования математических моделей на основе аппарата математического анализа.
Основные понятия:
первообразная, неопределенный интеграл, определенный интеграл, площадь криволинейной трапеции.
Контрольная работа № 5 по теме «Первообразная и интеграл».
4. Элементы комбинаторики, статистики и теории вероятностей. ( 11 ч )
Табличное и графическое представление данных. Числовые характеристики рядов данных. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. Элементарные сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статическая частота наступления события.
В результате изучения темы учащийся должен
знать/понимать:
-универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
- вероятностный характер различных процессов окружающего мира;
уметь:
- решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
- вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать в практической деятельности:
- анализ реальных числовых данных, представленных в виде диаграмм, графиков.
- анализ информации статического характера.
Основные понятия:
число перестановок, число сочетаний, число размещений, биномиальные коэффициенты, сложные события, несовместные события, вероятность события.
Контрольная работа № 6 по теме «Элементы комбинаторики, статистики и теории вероятностей»
5. Уравнения и неравенства. Системы уравнений и неравенств. ( 17 ч )
Равносильность уравнений. Основные методы решения уравнений. Решение систем уравнений. Основные приемы решения систем уравнений: подстановка; алгебраическое сложение; введение новых переменных. Общие методы решения неравенств. Метод интервалов. Решение систем неравенств с одной переменной. Использование свойств и графиков функций при решении уравнений и неравенств.
В результате изучения темы учащийся должен
знать/понимать:
- основные способы решения систем уравнений;
- алгоритмы решения уравнений и неравенств;
уметь:
- решать рациональные, показательные, логарифмические, тригонометрические и иррациональные уравнения и их системы;
- решать рациональные, показательные и логарифмические неравенства;
- решать простейшие уравнения и неравенства, содержащие знак модуля;
- решать уравнения, системы уравнений, неравенства используя свойства функций и их графические представления;
- решать текстовые задачи с помощью составления уравнений, интерпретируя результата с учетом ограничений условия задачи;
использовать в практической деятельности:
- построение и исследование простейших математических моделей;
приобретать опыт:
- планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов при изменении определенных условий.
Основные понятия:
равносильность уравнений, равносильность неравенств, равносильность систем.
Контрольная работа № 7 по теме «Уравнения и неравенства. Системы уравнений и неравенств»
6. Повторение (6 ч).
Решение текстовых задач. Преобразования графиков. Чтение графиков. Тригонометрические функции. Тригонометрические уравнения. Преобразования тригонометрических выражений. Применение производной. Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Обратная функция. Область определения и область значений обратной функции. График обратной функции.
Содержание учебного предмета
Модуль «Геометрия» 10 класс
1. Введение (аксиомы стереометрии и их следствия). (4 ч)
Предмет стереометрии. Основные понятия стереометрии (точка, прямая, плоскость, пространство). Аксиомы стереометрии. Некоторые следствия из аксиом. Решение задач на применение аксиом стереометрии и их следствий.
В результате изучения темы учащийся должен
знать/понимать:
- основные понятия и аксиомы стереометрии;
уметь:
- использовать знания при решении стандартных задач логического характера.
Основные понятия:
стереометрия, аксиомы стереометрии.
2. Параллельность прямых и плоскостей. (16 ч)
2.1. Параллельность прямых, прямой и плоскости.
Параллельность прямых, прямой и плоскости. Параллельные прямые в пространстве. Параллельность трех прямых. Параллельность прямой и плоскости.
В результате изучения темы учащийся должен
знать/понимать:
-определения параллельности прямых, параллельности прямой и плоскости в пространстве;
уметь:
- использовать метод доказательства от противного;
использовать в практической деятельности:
- различные способы изображения пространственных фигур на плоскости.
Основные понятия:
параллельные прямые в пространстве, параллельность прямой и плоскости.
2.2. Взаимное расположение прямых и плоскостей в пространстве.
Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой. Углы с сонаправленными сторонами. Угол между прямыми. Параллельные плоскости. Признак параллельности двух плоскостей. Свойства параллельных плоскостей.
В результате изучения темы учащийся должен
знать/понимать:
-определения скрещивающихся прямых, угла между прямыми, параллельности плоскостей в пространстве;
уметь:
- применять изученные теоремы к решению задач.
Основные понятия:
скрещивающиеся прямые, сонаправленные лучи, угол между прямыми, параллельность плоскостей.
Контрольная работа № 1 по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»
2.3. Тетраэдр и параллелепипед.
Тетраэдр. Параллелепипед. Свойства граней и диагоналей параллелепипеда. Задачи на построение сечений. Повторение теории, решение задач по теме.
В результате изучения темы учащийся должен
знать/понимать:
-определения призмы, пирамиды, правильных многогранников;
уметь:
- решать задачи с использованием понятий: угол между прямой и плоскостью, двугранный угол;
использовать в практической деятельности:
- свойства многогранников.
Основные понятия:
тетраэдр, параллелепипед, элементы многогранников (грани, вершины, ребра, диагонали).
Контрольная работа № 2 по теме «Параллельность прямых и плоскостей»
Зачет №1 по теме «Параллельность прямых и плоскостей»
3. Перпендикулярность прямых и плоскостей. (17 )
3.1. Перпендикулярность прямой и плоскости.
Перпендикулярность прямой и плоскости. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости. Признак перпендикулярности прямой и плоскости. Теорема о прямой, перпендикулярной к плоскости. Решение задач на перпендикулярности прямой и плоскости.
В результате изучения темы учащийся должен
знать/понимать:
- определения перпендикулярности прямых и плоскостей в пространстве;
уметь:
- использовать теоремы при решении задач;
использовать в практической деятельности:
- умение решать стереометрические задачи данной тематики.
Основные понятия:
перпендикулярные прямые в пространстве, перпендикулярность прямой и плоскости.
3.2. Перпендикуляр и наклонные. Угол между прямой и плоскостью.
Перпендикуляр и наклонные. Расстояние от точки до плоскости, расстояние от прямой до плоскости, расстояние между параллельными плоскостями, расстояние между скрещивающимися прямыми. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Параллельное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур.
В результате изучения темы учащийся должен
знать/понимать:
- определения перпендикуляра и наклонной к плоскости;
уметь:
- использовать теоремы при решении задач;
использовать в практической деятельности:
- умение решать стереометрические задачи данной тематики.
Основные понятия:
перпендикуляр, наклонная, проекция наклонной, угол между прямой и плоскостью.
3.3 Двугранный угол. Перпендикулярность плоскостей.
Двугранный угол, линейный угол двугранного угла. Признак перпендикулярности двух плоскостей. Прямоугольный параллелепипед. Повторение теории, решение задач по всей теме.
В результате изучения темы учащийся должен
знать/понимать:
- определения двугранного угла, перпендикулярности плоскостей в пространстве;
уметь:
- применять при решении задач сведения, полученные из курса планиметрии.
Основные понятия:
двугранный угол, перпендикулярность плоскостей, прямоугольный параллелепипед.
Контрольная работа № 3 по теме «Перпендикулярность прямых и плоскостей»
Зачет №2 по теме «Перпендикулярность прямых и плоскостей»
4. Многогранники. (12 ч)
Понятие многогранника. Вершины, ребра, грани многогранника.
Призма, ее основания, боковые ребра, высота, площадь поверхности призмы.
Пирамида. Правильная пирамида ее основание, боковые ребра, высота. Треугольная пирамида. Усеченная пирамида. Площадь поверхности пирамиды. Правильные многогранники (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр). Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников.
В результате изучения темы учащийся должен
знать/понимать:
- определения основных видов многогранников;
уметь:
- использовать представления многогранников и их свойства при решении задач;
использовать в практической деятельности:
- умение пользоваться формулами и понятиями при решении задач.
Основные понятия:
многогранник, элементы многогранника (вершины, ребра, грани, диагонали), призма, виды призм, площади полной и боковой поверхностей, пирамида, виды пирамид, правильные многогранники.
Контрольная работа № 4 по теме «Многогранники»
Зачет №3 по теме «Многогранники. Площадь поверхности призмы и пирамиды»
5. Заключительное повторение тем геометрии 10 класса. (5 ч)
Аксиомы стереометрии и их следствия. Параллельность прямых и плоскостей. Перпендикулярность прямых и плоскостей. Многогранники. Заключительный урок-беседа по курсу геометрии 10 класса
Содержание учебного предмета
Модуль «Геометрия» 11 класс
1. Векторы в пространстве. (5 ч)
Понятие вектора. Модуль вектора. Равенство векторов. Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. Компланарные векторы. Правило параллелепипеда. Разложение вектора по трем некомпланарным векторам. Повторение теории, решение задач по теме.
В результате изучения темы учащийся должен
знать/понимать:
- правила действий с векторами в пространстве;
уметь:
- применять материал о векторах на плоскости, изученный в базовой школе, для выполнения действий с векторами в пространстве;
использовать в практической деятельности:
- векторный метод для решения задач.
Основные понятия:
вектор, нулевой вектор, длина вектора, коллинеарность векторов, равенство векторов, действия над векторами, компланарные векторы, правило параллелепипеда.
2. Метод координат в пространстве. (15 ч)
2.1. Координаты точки и координаты вектора.
Декартовы координаты в пространстве. Координаты точки и координаты вектора. Прямоугольная система координат в пространстве. Связь между координатами векторов и координатами точек. Простейшие задачи в координатах.
В результате изучения темы учащийся должен
знать/понимать:
- определения координат вектора в пространстве;
уметь:
- строить точки и векторы в прямоугольной системе координат в пространстве;
использовать в практической деятельности:
- метод координат при решении задач.
Основные понятия:
прямоугольная система координат в пространстве, координаты точки, единичный вектор, координаты вектора.
Контрольная работа №1 по теме «Простейшие задачи в координатах»
2.2. Скалярное произведение векторов.
Угол между векторами. Скалярное произведение векторов. Вычисление углов между прямыми и плоскостями. Скалярное произведение векторов Коллинеарные векторы. . Разложение векторов по двум неколлинеарным векторам.
В результате изучения темы учащийся должен
знать/понимать:
- формулу скалярного произведения векторов;
уметь:
- вычислять скалярное произведение векторов.
Основные понятия:
угол между векторами, скалярное произведение векторов, направляющий вектор прямой.
2.3. Движения.
Понятие о симметрии в пространстве Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос. Примеры симметрий в окружающем мире.
В результате изучения темы учащийся должен
знать/понимать:
- определения движений;
уметь:
- применять движения при решении задач.
Основные понятия:
движение, виды движений (центральная симметрия, осевая симметрия, зеркальная симметрия, параллельный перенос).
Контрольная работа №2 по теме «Скалярное произведение векторов в пространстве. Движение»
Зачет по теме «Метод координат в пространстве»
3. Цилиндр, конус и шар (11 ч)
Цилиндр. Основание, высота, боковая поверхность, образующая, развертка цилиндра. Площадь поверхности цилиндра. Осевые сечения и сечения, параллельные основанию
Конус. Основание, высота, боковая поверхность, образующая, развертка конуса. Площадь поверхности конуса. Усеченный конус. Осевые сечения и сечения, параллельные основанию.
Сфера и шар.. Уравнение сферы. Взаимное расположение сферы и плоскости. Сечения сферы и шара. Касательная плоскость к сфере. Площадь сферы. Решение задач на многогранники, цилиндр, конус и шар.
В результате изучения темы учащийся должен
знать/понимать:
- определения основных видов тел вращения;
уметь:
- изображать тела вращения на плоскости;
- решать задачи на вычисление площадей поверхностей тел вращения;
использовать в практической деятельности:
- формулы площадей для решения практических задач.
Основные понятия:
цилиндр, элементы цилиндра, конус, элементы конуса, усеченный конус, сфера, шар, касательная плоскость к сфере, площадь поверхности тел.
Контрольная работа №3 по теме «Тела вращения»
4. Объемы тел. (16 ч)
Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема прямоугольного параллелепипеда, куба, прямой призмы, основанием которой является прямоугольный треугольник. Формулы объема прямой призмы и цилиндра. Вычисление объемов тел с помощью определенного интеграла. Объем наклонной призмы. Объем пирамиды. Объем конуса. Объем шара. Объем шарового сегмента, шарового слоя и шарового сектора. Площадь сферы.
В результате изучения темы учащийся должен
знать/понимать:
- понятие объема тела;
- формулы объемов тел;
уметь:
- находить объем тела по формуле и с помощью интеграла;
- решать задачи на вычисление объемов тел;
использовать в практической деятельности:
- формулы объемов для решения практических задач.
Основные понятия:
объем тел.
Контрольная работа №4 по темам: «Объем шара и его частей», «Площадь сферы».
Зачет по теме «Объемы тел»
5. Заключительное повторение при подготовки учащихся к итоговой аттестации по геометрии. (8 ч)
Аксиомы стереометрии. Параллельность прямых, прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей. Двугранный угол. Перпендикулярность плоскостей. Многогранники: параллелепипед, призма, пирамида, площади их поверхностей. Векторы в пространстве. Действия над векторами. Скалярное произведение векторов. Цилиндр, конус и шар, площади их поверхностей. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Объемы тел.
Информационные источники
«Алгебра»
Литература для учителя
Мордкович А.Г. Алгебра и начала математического анализа. 10-11кл.: В двух частях. Учеб. для учащихся общеобразоват. учреждений. – М.: Мнемозина, 2009 г.
Мордкович А.Г. Алгебра и начала математического анализа. 10-11кл.: В двух частях. Задачник для общеобразоват. учреждений. – М.: Мнемозина, 2009 г.
Алгебра и начала математического анализа. 10 класс. Контрольные работы для учащихся общеобразоват. учреждений / В.И. Глизбург; под ред А.Г. Мордковича. – Москва: Мнемозина, 2009.
Алгебра и начала математического анализа. 11 класс. Контрольные работы для учащихся общеобразоват. учреждений / В.И. Глизбург; под ред А.Г. Мордковича. – Москва: Мнемозина, 2009.
Алгебра и начала математического анализа. 10 класс. Самостоятельные работы для учащихся общеобразоват. учреждений / Л.А. Александрова; под ред А.Г. Мордковича. – Москва: Мнемозина, 2008.
Алгебра и начала математического анализа. 11 класс. Самостоятельные работы для учащихся общеобразоват. учреждений / Л.А. Александрова; под ред А.Г. Мордковича. – Москва: Мнемозина, 2009.
Алгебра и начала математического анализа. 10 – 11 классы.Методическое пособие для учителя / А.Г. Мордкович, П.В.Семенов – Москва: Мнемозина, 2010.
Федеральный компонент государственного стандарта общего образования. Математика / Министерство образования Российской Федерации. – Москва, 2004.
Бобкова Л.Г. Проектирование рабочей программы по учебному предмету / ИПКиПРО Курганской области. – Курган, 2006.
Закон «Об образовании»
Математика. Примерные программы на основе Федерального компонента государственного стандарта основного и среднего (полного) общего образования / Министерство образования и науки Российской Федерации. – Москва, 2005.
Литература для обучающихся
Мордкович А.Г. Алгебра и начала математического анализа. 10-11кл.: В двух частях. Учеб. для учащихся общеобразоват. учреждений. – М.: Мнемозина, 2009 г.
Мордкович А.Г. Алгебра и начала математического анализа. 10-11кл.: В двух частях. Задачник для общеобразоват. учреждений. – М.: Мнемозина, 2009 г.
Алгебра и начала математического анализа. 10 класс. Контрольные работы для учащихся общеобразоват. учреждений / В.И. Глизбург; под ред А.Г. Мордковича. – Москва: Мнемозина, 2009.
Алгебра и начала математического анализа. 11 класс. Контрольные работы для учащихся общеобразоват. учреждений / В.И. Глизбург; под ред А.Г. Мордковича. – Москва: Мнемозина, 2009.
Алгебра и начала математического анализа. 10 класс. Самостоятельные работы для учащихся общеобразоват. учреждений / Л.А. Александрова; под ред А.Г. Мордковича. – Москва: Мнемозина, 2008.
Алгебра и начала математического анализа. 11 класс. Самостоятельные работы для учащихся общеобразоват. учреждений / Л.А. Александрова; под ред А.Г. Мордковича. – Москва: Мнемозина, 2009.
«Геометрия»
Литература для учителя
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. / Геометрия: учебник для 10 – 11 кл. общеобразоват. учреждений – М.: Просвещение, 2010.
Зив Б.Г. / Дидактические материалы по геометрии. 10 класс. – М.: Просвещение, 2009.
Зив Б.Г. / Дидактические материалы по геометрии. 11 класс. – М.: Просвещение, 2008.
Саакян С.М. Изучение геометрии в 10 – 11 классах./ кн. для учителя. М.: Просвещение, 2010.
Яровенко В.А. Поурочные разработки по геометрии: 10 класс. М.: ВАКО, 2010.
Яровенко В.А. Поурочные разработки по геометрии: 11 класс. М.: ВАКО, 2010.
Программы для общеобразовательных школ, гимназий, лицеев: Математика. 5 – 11 кл. / Сост. Г.М. Кузнецова, Н.Г.Миндюк. – 3-е изд., стереотип. – М.: Дрофа, 2002.
Федеральный компонент государственного стандарта общего образования. Математика / Министерство образования Российской Федерации. – Москва, 2004.
Литература для обучающихся
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. / Геометрия: учебник для 10 – 11 кл. общеобразоват. учреждений – М.: Просвещение, 2010.
ЕГЭ 2012 Математика. Типовые тестовые задания / И.П.Высоцкий и др. под ред. А.Л.Семенова, И.В.Ященко. – М.: Издательство «Экзамен»
ЕГЭ 2012 Математика: типовые экзаменационные варианты: 30 вариантов / под ред. А.Л.Семенова, И.В.Ященко. – М.: Национальное образование, 2011
Список образовательных ресурсов Сети Интернет
● geometr.info "Мир геометрии" - портал для школьников, абитуриентов и студентов (теория, задачи по геометрии). Помощь в решении задач по геометрии (можно прислать задачу для решения) и др.
● bymath.net - "Вся элементарная математика" Средняя математическая Интернет-школа. Темы: Арифметика, Алгебра, Геометрия, Тригонометрия, Функции и графики, Основы анализа, Множества, Вероятность, Аналитическая геометрия. Все темы содержат множество примеров с решениями.
● school.msu.ru - школьный консультационный сайт "Математика" для информационной поддержки учителей и учеников.
● math.ru - сайт Math.ru, учредитель - МЦНМО. На сайте - очень приличная Библиотека, Учительская - перечни, постановления, стандарты.
● college.ru - раздел "Открытого колледжа" - "Математика". Включает иллюстрированные учебники: "Алгебра 2.6", "Планиметрия 2.5", "Стереометрия 2.5", "Функции и графики" (для открытия решения или доказательства использовать левую кнопку мышки).
● kvant.mccme.ru - Научно-популярный физико-математический журнал "Квант" Статьи, задачи с решениями. Калейдоскоп "Кванта"; Школа в "Кванте". По страницам школьных учебников (математика). Математический кружок.
● potential.org.ru - "Потенциал" - образовательный журнал для старшеклассников и учителей. Раздел "Математика".
● bobych.ru - Алгебра. Геометрия. Тригонометрия. (электронные учебники)
● shevkin.ru - проект "Математика. Школа. Будущее". Сайт учителя математики, кандитата педагогических наук, автора учебников и пособий по математике Шевкина А.В. На сайте - множество актуальных статей, консультации, полезные советы, о подготовке к ЕГЭ и др.
● graphfunk.narod.ru - "Графики функций". Небольшой сайт в помощь школьнику, изучающему графики функций: определения, примеры, задачник.
● courier.com.ru - "Игра в обучение математике". Сборник нестандартных задач. Ю.А. Глазков. (Арифметика, алгебра, геометрия, физика). Для учителей.
● comp-science.narod.ru - Учителям информатики и математики и их любознательным ученикам (дидактические материалы по информатике и математике).
● etudes.ru - сайт "Математические этюды" На сайте представлены этюды, выполненные с использованием современной компьютерной 3D-графики, увлекательно и интересно рассказывающие о математике и ее приложениях
● methmath.chat.ru - Методика преподавания математики. Темы: исследование функций, тригонометрические неравенства, преобразования графиков.
● courier.com.ru - для учителей. "Поурочное планирование учебного материала по математике" И.К. Варшавский.
Контрольно – измерительные материалы
Модуль «Алгебра и начала анализа» 11 класс
Источник: Алгебра и начала математического анализа. 11 класс. Контрольные работы для учащихся общеобразоват. учреждений / В.И. Глизбург; под ред А.Г. Мордковича. – Москва: Мнемозина, 2009.
Контрольные работы подготовлены для тех учащихся, которые изучают курс алгебры и начал математического анализа в 10 классе по учебному комплекту, соответствующему базовому уровню образовательного стандарта:
Мордкович А.Г. Алгебра и начала математического анализа. 10-11кл.: В двух частях. Учеб. для учащихся общеобразоват. учреждений. – М.: Мнемозина, 2009 г.
Мордкович А.Г. Алгебра и начала математического анализа. 10-11кл.: В двух частях. Задачник для общеобразоват. учреждений. – М.: Мнемозина, 2009 г.
Каждая контрольная состоит из четырех вариантов. Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума – до первой черты, задания среднего уровня – между первой и второй чертой, задания уровня выше среднего – после второй черты. Шкала оценок за выполнение контрольной работы выглядит так: за успешное выполнение только заданий обязательного минимума – оценка 3; за успешное выполнение заданий обязательного минимума и одного дополнительного (после первой или второй черты) – оценка 4; за успешное выполнение заданий всех трех уровней – оценка 5.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (10 класс) (0.36 MB)
Рабочая программа по математике (10 класс) (0.36 MB)
 0
0 772
772 10
10 Нравится
0
Нравится
0


