Ход урока
| № | Действия учителя
| Действия учащихся | Методы обучения | Средства обучения | Формы обучения |
| 1 | Учитель заходит в класс и приветствует учеников. | Ученики приветствуют учителя. |
|
|
|
| 2 | -Сегодня на уроке мы будем решать задачи которые встречаются в заданиях ЕГЭ на производную, а именно задания типа В 14; -Слайд 1 Запишите тему занятия: «Подготовка к ЕГЭ. В14».
| Записывают тему занятия. | Объяснение |
| Фронтальная |
|
3 | 1.Начнем с задач на геометрический смысл производной. В чем заключается геометрический смысл производной? 2. Слайд 3 Когда функция возрастает на интервале? Когда функция убывает на интервале?
3. Слайд 4 Давайте посмотрим графическую интерпретацию точек максимума и минимума функции.
| 1. Ученики отвечают устно: Производная в точке 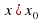 равна угловому коэффициенту касательной или тангенсу угла наклона касательной; равна угловому коэффициенту касательной или тангенсу угла наклона касательной; 2. f(x) дифференцируема на интервале (a;b) Если f′(x)0 в каждой точке интервала, то функция y=f(x) возрастает на этом интервале. Если f′(x)y=f(x) убывает на этом интервале. 3.Ученики делают краткую иллюстрацию в тетрадях.
| Опрос |
| Фронтальная |
|
4 | 1.Слайд 5 Найдите точку минимума функции y = x3 – 48x + 17 Правильный ответ 4. Сравните решение с решением представленном на слайде. 2.Слайд 6 Решите самостоятельно: Найдите точку максимума функции 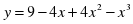
Проверьте себя, сравнив ваше решение с решением показанным на слайде.
3.Слайд 7 Решите самостоятельно: Найдите точку максимума функции 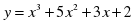
Проверьте себя, сравнив ваше решение с решением показанным на слайде.
4. Слайд 8 Найдите точку минимума функции 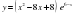
5. Слайд 9 Найдите точку минимума функции 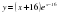
6. Слайд 10 Найдите точку минимума функции 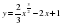
7. Слайд 11 Найдите точку максимума функции
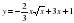
8. Слайд 12 Найдите точку максимума функции 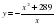
9. Слайд 13 Найдите точку минимума функции
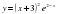
Решите самостоятельно:
10. Слайд 14 Найдите наименьшее значение функции y = 3x2 – 2x3 + 1 на отрезке [-4;0] по схеме представленной на слайде. 11. Слайд 15 Найдите наибольшее значение функции 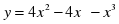
на отрезке [1;3] Проверьте себя, посмотрев на слайд.
12. Слайд 16 Решите самостоятельно: Найдите наименьшее значение функции на отрезке [-2;2] 
13. Слайд 17 Найдите наибольшее значение функции на отрезке [-1;7]
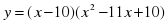
| 1.Учащиеся читают задачу и разбирают условие. Ученик выполняет задание у доски по плану, показанному на слайде презентации
2.Ученики решают самостоятельно в тетрадях D(y)=(-∞;+∞) 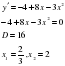
Ответ:2
3. Ученики решают самостоятельно 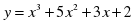
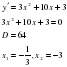
Ответ: -3
4. Ученик решает у доски: 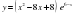
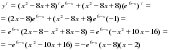
Ответ: 2.
5.Ученик решает у доски: 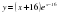
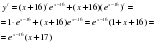
Ответ: -17
6. Ученик решает у доски: 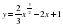
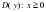
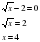
Ответ: 4
7. Ученик решает у доски: 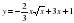
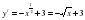
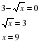
Ответ: 9 8. Ученик решает у доски: 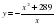

 
Ответ: 17
9. Ученик решает у доски:  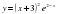
Ответ: -3
10,11,12,13 Ученики решают самостоятельно в тетрадях, сравнивая решение с ответом показанным на слайде.
| Упражнение
Работа у доски, упражнение
Самостоятельная работа, упражнения | Презентация
Презентация, доска | Фронтальная, индивидуальная
Индивидуальная |
| 5,6 | Учитель объявляет оценки за урок и домашнее задание. Домашнее задание: 1.Исследовать на экстремум функцию 2.Найти наибольшее и наименьшее значение функции 
| Ученики записывают задание на дом. Те кто получил оценки подают дневник.
|
|
|
|
Конспект урока
Тема: «Подготовка к ЕГЭ. В14».
Класс: 11 класс (физико-математический профиль).
Тип урока: Урок применения знаний на практике.
Цели урока:
Обучающие: Обобщить и закрепить материал по теме «Производная и ее применение». Рассмотреть задания типа В 14.
Развивающие: развитие аналитического мышления учащихся; формирование умения выделять главное и обобщать.
Воспитывающие: формирование умения организовать свою деятельность; формирование аккуратности записей и чертежей в тетради при самостоятельной работе.
Оборудование: доска, проектор, презентация.
Литература: рабочая тетрадь С.А. Шестакова «ЕГЭ 2012. Математика. Задача В14. Исследование функции»
План урока
Организационный момент (2 мин.)
Постановка цели (1 мин.)
Актуализация знаний (8 мин.)
Оперирование ЗУН при решении практических задач(30 мин.)
Подведение итогов (2 мин.)
Сообщение домашнего задания и инструктаж по его выполнению (2 мин.)
Анализ урока
Школа гимназия №1 Дата Класс 11
Количество учащихся На уроке Предмет
ФИО учителя
Тема: Подготовка к ЕГЭ. В14
Тип урока: применение знаний на практике.
Цели урока:
Обучающие: Обобщить и закрепить материал по теме «Производная и ее применение». Рассмотреть задания типа В 14.
Развивающие: развитие аналитического мышления учащихся; формирование умения выделять главное и обобщать.
Воспитывающие: формирование умения организовать свою деятельность; формирование аккуратности записей и чертежей в тетради при самостоятельной работе.
В ходе урока они были достигнуты.
2. Учитель и учащиеся были хорошо подготовлены к уроку, время распределено грамотно, урок соответствовал своему типу и соответствовал плану урока данного типа. На этапе актуализации были повторены все формулы и определения. На этапе оперирования ЗУН учитель грамотно направлял учащихся к нахождению решения задачи. На этапе подведения итогов было сообщено домашнее задание.
3. Материал, изложенный учителем соответствует всем принципам дидактики, а именно, Научность, доступность, наглядность, абстрактность, систематичность и последовательность.
4. Объем фактически изложенного материала соответствует программе профильного обучения, на базе теоретического материала решены задачи на построение. Текущий материал связан с ранее изученным тем, что он является его логическим продолжением.
5. Основными методами обучения на уроке были: опрос и упражнение. Они являются очень эффективными как для фронтальной формы обучения, так и для индивидуальной, которые были использованы на уроке. Дети вели себя очень активно и эрудированно.
6. Взаимоотношения учителя и ученика доверительные. Учитель является своеобразным проводником к знаниям.
7. Все санитарно – гигиенические нормы соблюдены.
8. Материал был понят и усвоен детьми.

 Получите свидетельство
Получите свидетельство Вход
Вход


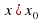 равна угловому коэффициенту касательной или тангенсу угла наклона касательной;
равна угловому коэффициенту касательной или тангенсу угла наклона касательной;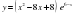
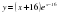
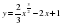
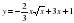
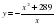
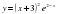
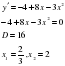
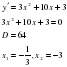
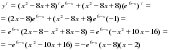
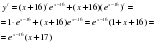
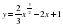
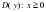
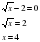
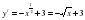
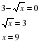









 Производная и ее применение (87.81 КB)
Производная и ее применение (87.81 КB)
 0
0 520
520 19
19 Нравится
0
Нравится
0





