Самостоятельная работа по математике "Производная"

Презентация содержит самостоятельную работу на два варианта. Задания взяты из сайта «Решу ЕГЭ» по темам «Вычисление производных», «Геометрический смысл производной», «Применение производной для исследования функций на монотонность и экстремумы», «Нахождение наибольшего и наименьшего значений на отрезке».

Презентация содержит восемь слайдов.

Самостоятельная работа по теме «Производная» (подготовка к ЕГЭ задания В9, В15)

Производная

Вариант 1.

Вариант 1.

Вариант 2.

1.Найти производную функции:

Вариант 2.

1.Найти производную функции:

А) у= - 7х;

А) у= - 5 ;

Б) у= ;

Б) у= ;

В) у = .

В) у = tg 2х.

Производная

Вариант 1.

Вариант 1.

Вариант 2.

2. Материальная точка движется прямолинейно по закону

Вариант 2.

х(t) = 6 - 48t + 17

2. Материальная точка движется прямолинейно по закону

(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения).

x( t) = - - 2 +5t +13

(где x — расстояние от точки от­счета в метрах, t — время в секундах, измеренное с начала движения).

Найдите ее скорость (в м/с) в момент времени t = 9 с.

Найдите ее скорость (в м/с) в момент времени t = 3 с.

Производная

Вариант 1.

Вариант 2.

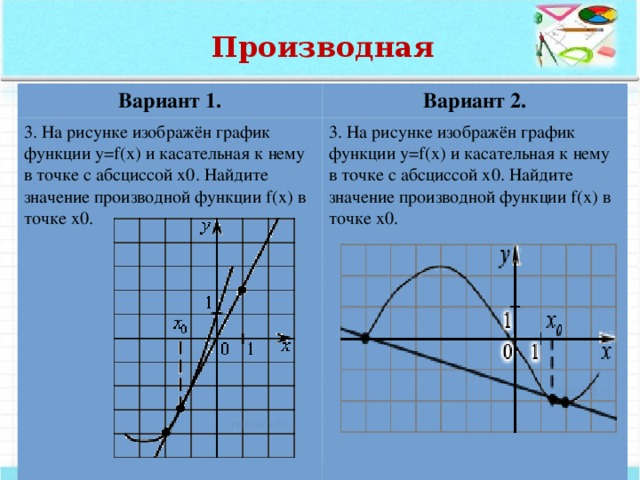
3. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

3. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

Производная

Вариант 1.

Вариант 2.

4. На рисунке изображен график функции у = f(x), определенной на интервале (−6; 8). Определите количе­ство целых точек, в которых производная функции положительна.

4. На рисунке изображен график производной функции , определенной на интервале ( -8; 3) . В какой точке отрезка [-3;2] функция принимает наибольшее значение?

Производная

Вариант 1.

Вариант 2.

5. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите ко­личество точек максимума функции f(x) на отрезке [−6; 9].

5. На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

Производная

Вариант 1.

Вариант 2.

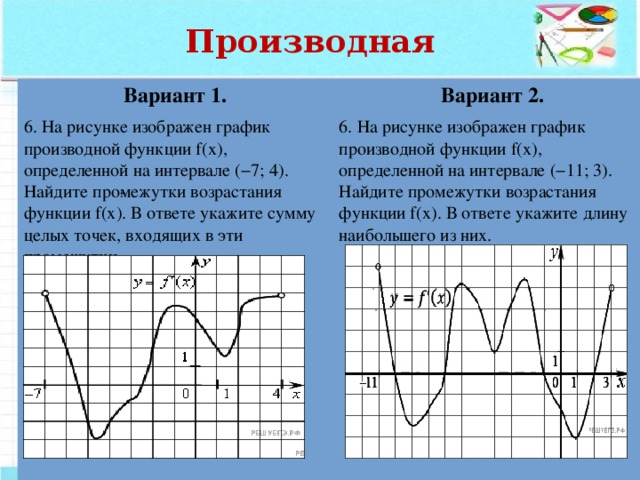
6. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите про­межутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

6. На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Производная

Вариант 1.

Вариант 1.

Вариант 2.

7.Найдите точку максимума функции у= - 48 х +17.

Вариант 2.

7. Найдите точку максимума функции у = + 2 + х + 3.

8.Найдите наименьшее значение функции

у = - 27х

8. Найдите наименьшее значение функции

на отрезке [0; 4].

у = 7 + 12х -

на отрезке [-2; 2].