
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Определение, построение, обозначение,
свойство.
Учитель Козина Н.А.

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Определение
Две прямые на плоскости называются параллельными, если они не пересекаются.

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Обозначение
a ║ b
a
b

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Построение
С помощью угольника и линейки
а
B
b

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Стр23. Две прямые перпендикулярные третьей – не пересекаются.
а
B
b
с
тест
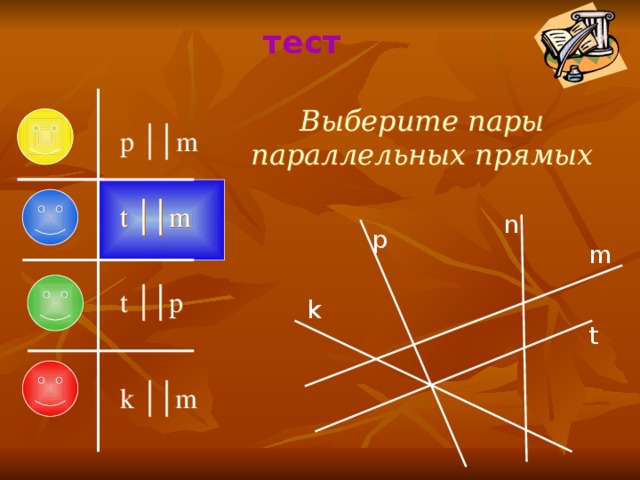
Выберите пары параллельных прямых
p ││m
t ││m
n
p
m
t ││p
k
t
k ││m
тест
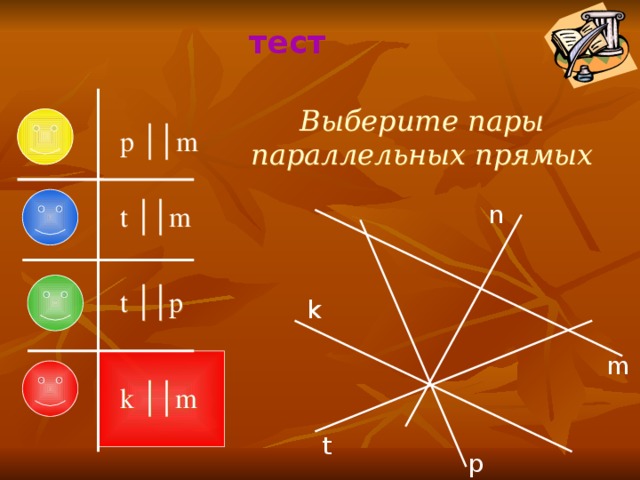
Выберите пары параллельных прямых
p ││m
t ││m
n
t ││p
k
m
k ││m
t
p
тест
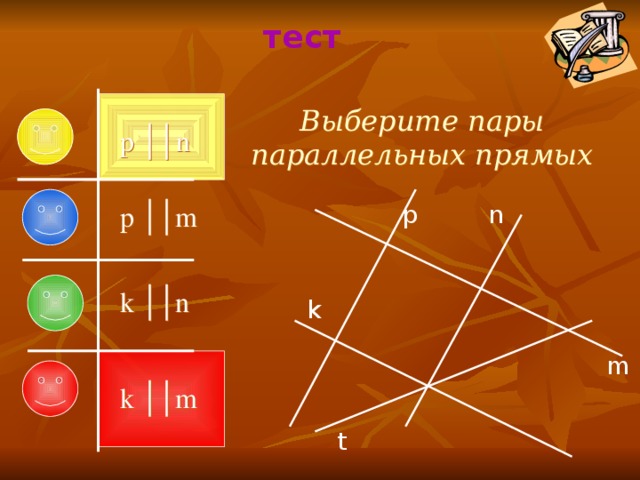
Выберите пары параллельных прямых
p ││n
p
p ││m
n
k ││n
k
m
k ││m
t
тест
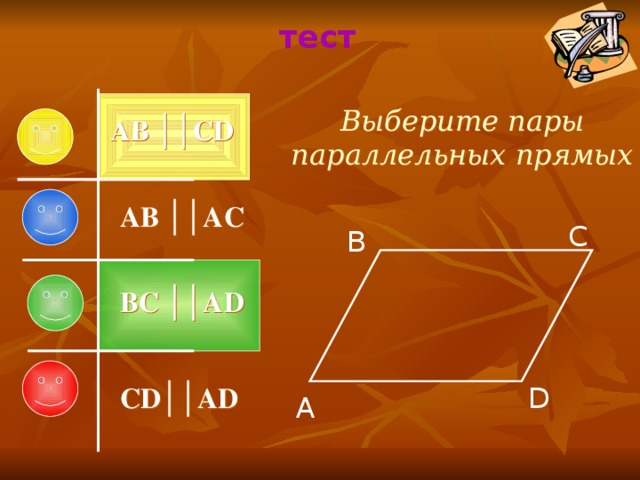
Выберите пары параллельных прямых
AB ││CD
AB ││AC
C
B
BC ││AD
CD ││AD
D
A

ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
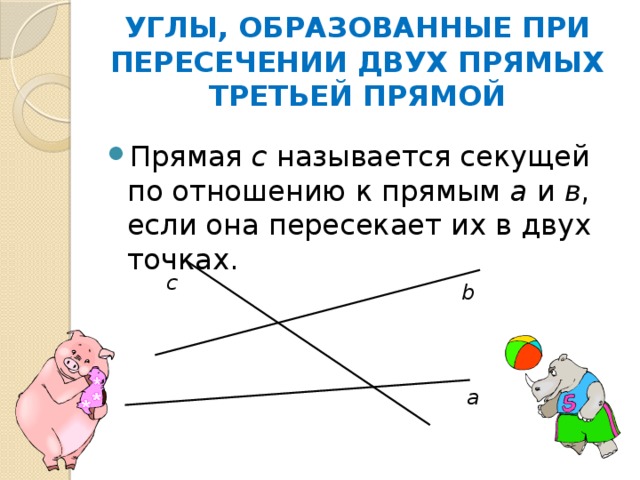
- Прямая с называется секущей по отношению к прямым а и в , если она пересекает их в двух точках.
с
b
а
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
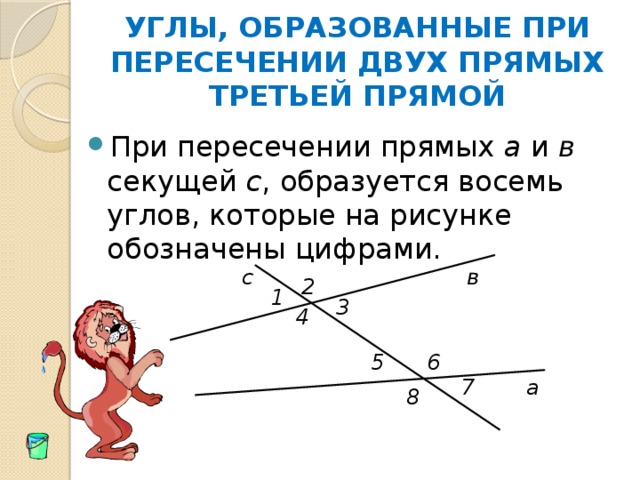
- При пересечении прямых а и в секущей с , образуется восемь углов, которые на рисунке обозначены цифрами.
с
в
2
1
3
4
5
6
а
7
8
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
5
6
7
а
8
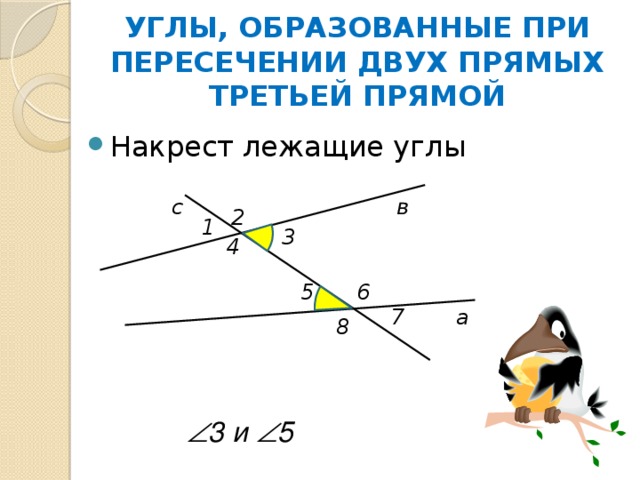
3 и 5
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
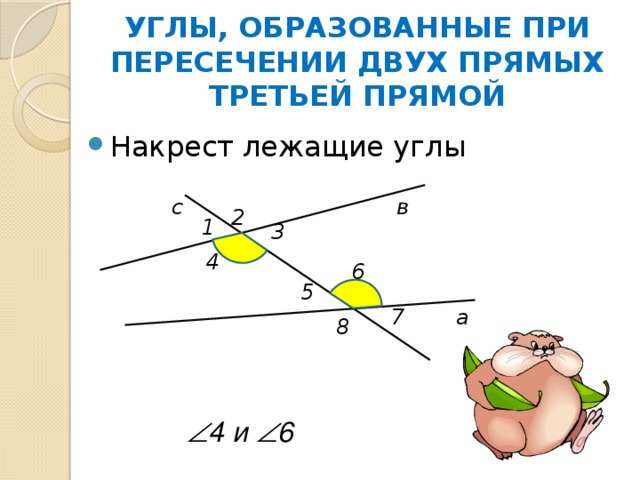
4 и 6
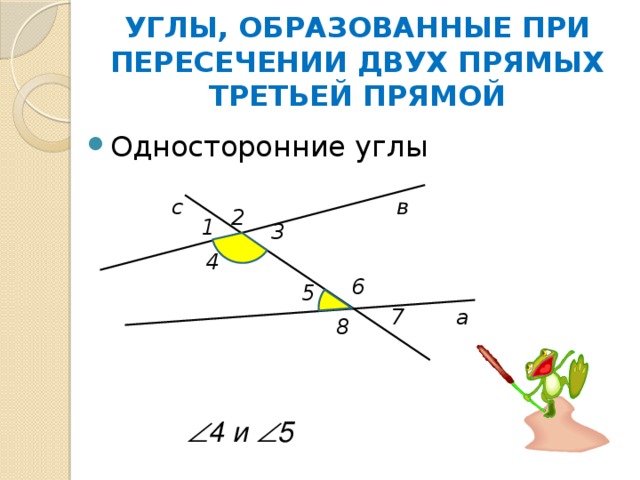
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
4 и 5
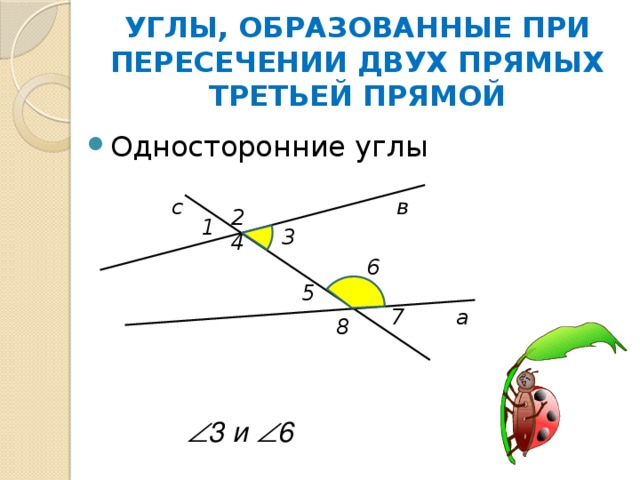
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
3 и 6
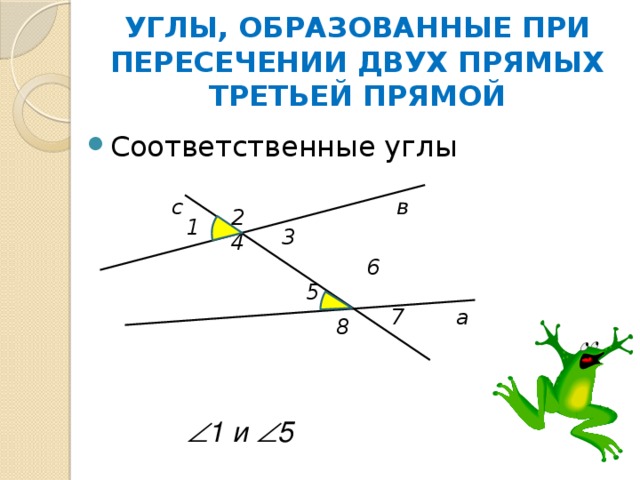
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
1 и 5
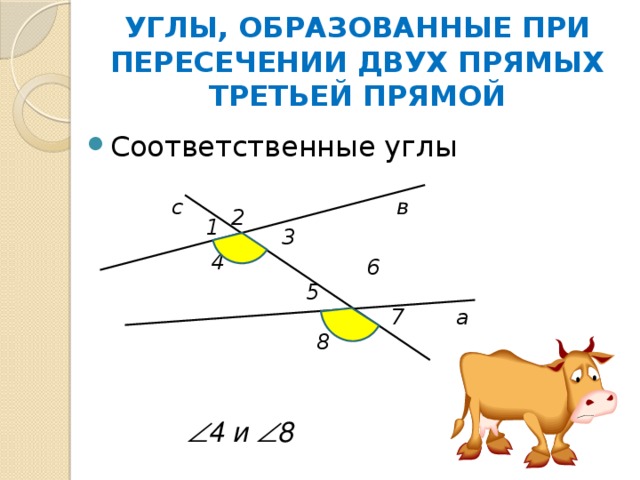
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
6
5
7
а
8
4 и 8
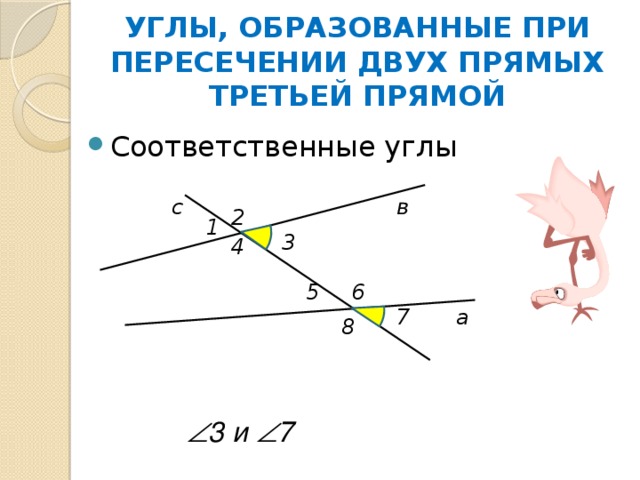
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
с
в
2
1
3
4
5
6
7
а
8
3 и 7
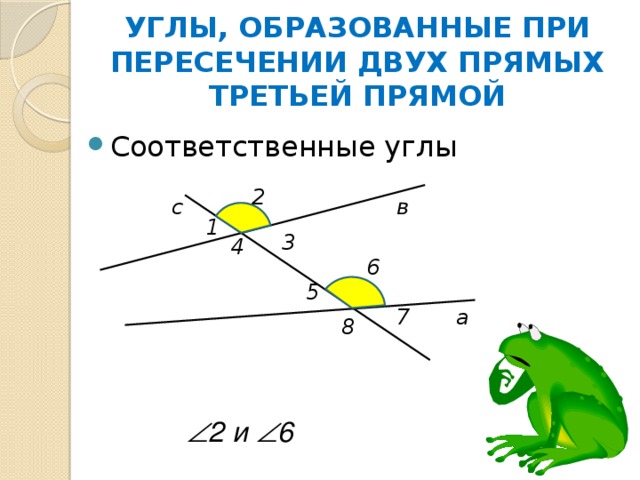
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
2
с
в
1
3
4
6
5
7
а
8
2 и 6
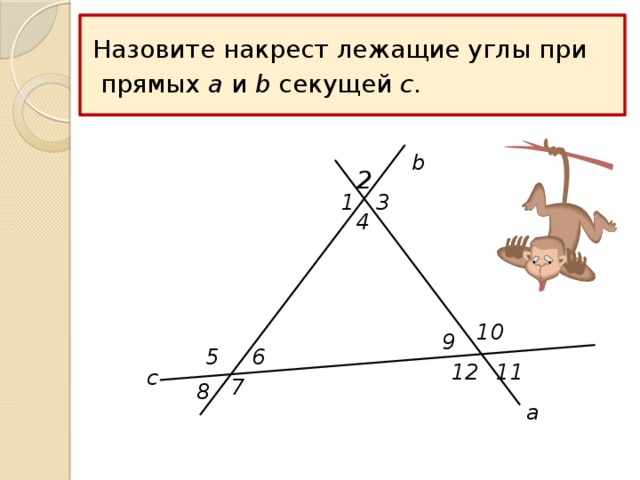
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
Назовите накрест лежащие углы при
прямых a и b секущей c .
b
2
1
3
4
10
9
5
6
11
12
с
7
8
а
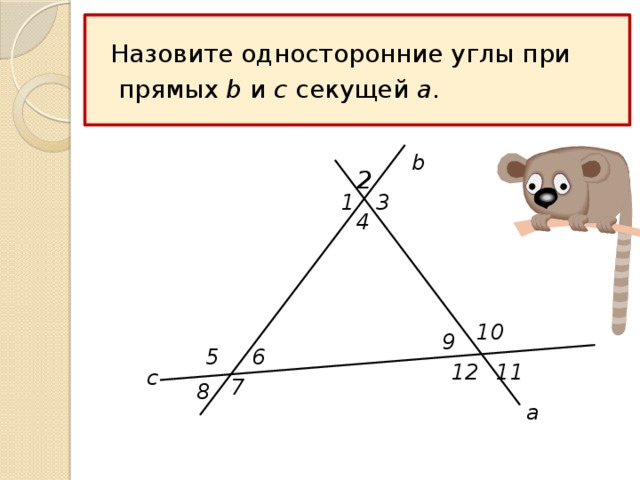
Назовите односторонние углы при
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
прямых b и c секущей a .
b
2
1
3
4
10
9
6
5
11
12
с
7
8
а
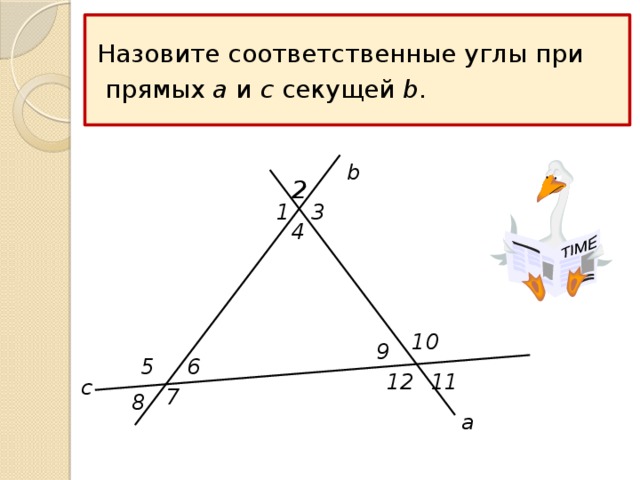
Назовите соответственные углы при
УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ ТРЕТЬЕЙ ПРЯМОЙ
прямых a и c секущей b .
b
2
3
1
4
10
9
6
5
11
12
с
7
8
а

ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ, ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
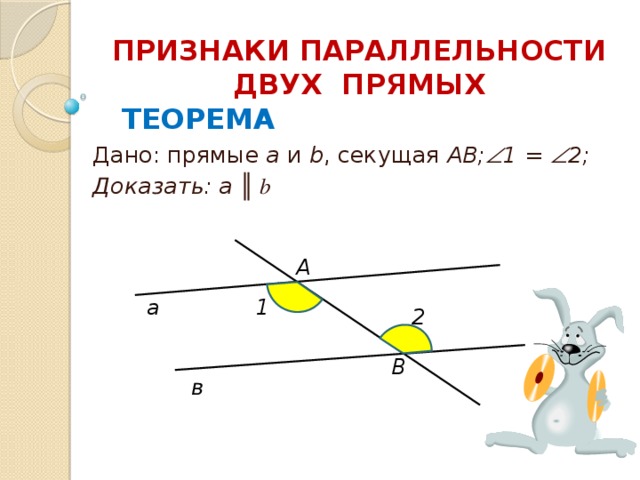
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ТЕОРЕМА
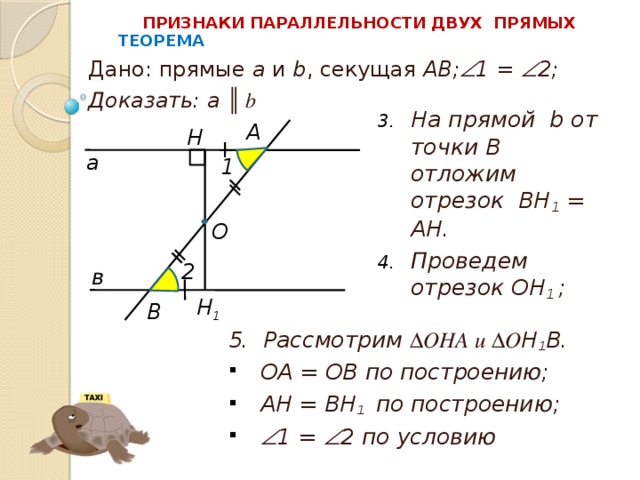
Дано: прямые a и b , секущая АВ; 1 = 2;
Доказать: а ║ b
А
1
а
2
В
в
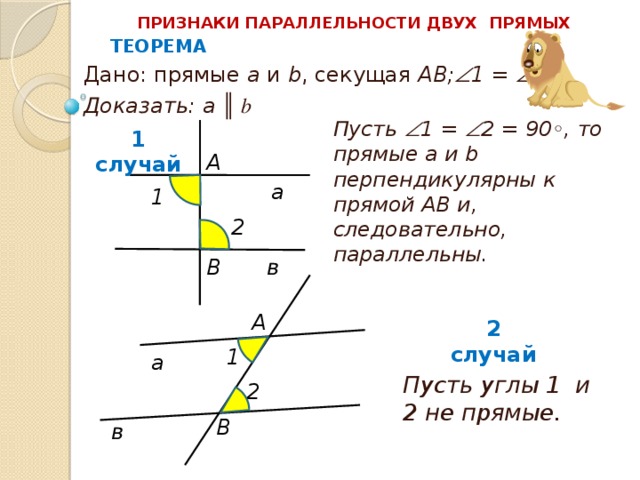
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ТЕОРЕМА
Дано: прямые a и b , секущая АВ; 1 = 2;
Доказать: а ║ b
Пусть 1 = 2 = 90 ◦, то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны.
1 случай
А
а
1
2
В
в
А
2 случай
1
а
Пусть углы 1 и 2 не прямые .
2
В
в
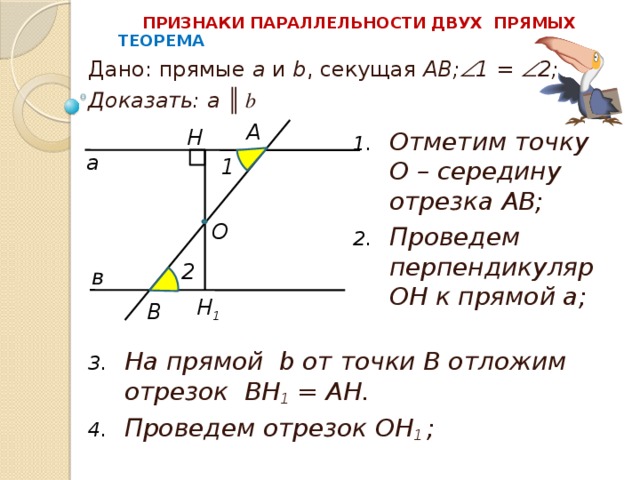
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ТЕОРЕМА
Дано: прямые a и b , секущая АВ; 1 = 2;
Доказать: а ║ b
А
H
- Отметим точку О – середину отрезка АВ;
- Проведем перпендикуляр OH к прямой а;
а
1
O
2
в
H 1
В
- На прямой b от точки В отложим отрезок ВН 1 = АН.
- Проведем отрезок ОН 1 ;
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ТЕОРЕМА
Дано: прямые a и b , секущая АВ; 1 = 2;
Доказать: а ║ b
- На прямой b от точки В отложим отрезок ВН 1 = АН.
- Проведем отрезок ОН 1 ;
А
H
а
1
O
2
в
H 1
В
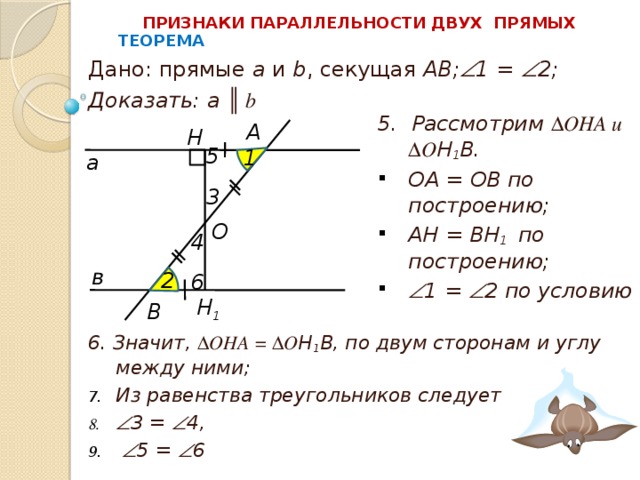
5. Рассмотрим ∆OHA и ∆О Н 1 В.
- ОА = ОВ по построению;
- АН = ВН 1 по построению;
- 1 = 2 по условию
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ТЕОРЕМА
Дано: прямые a и b , секущая АВ; 1 = 2;
Доказать: а ║ b
5. Рассмотрим ∆OHA и ∆О Н 1 В.
- ОА = ОВ по построению;
- АН = ВН 1 по построению;
- 1 = 2 по условию
А
H
5
1
а
3
O
4
в
2
6
H 1
В
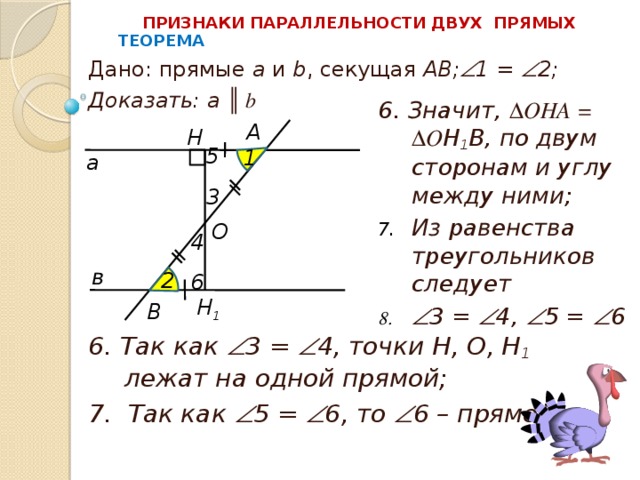
6. Значит, ∆OHA = ∆О Н 1 В, по двум сторонам и углу между ними;
- Из равенства треугольников следует
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ТЕОРЕМА
Дано: прямые a и b , секущая АВ; 1 = 2;
Доказать: а ║ b
6. Значит, ∆OHA = ∆О Н 1 В, по двум сторонам и углу между ними;
- Из равенства треугольников следует
А
H
5
1
а
3
O
4
в
2
6
H 1
В
6. Так как 3 = 4, точки Н, О, Н 1 лежат на одной прямой;
7. Так как 5 = 6, то 6 – прямой.
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ
ТЕОРЕМА
Дано: прямые a и b , секущая АВ; 1 = 2;
Доказать: а ║ b
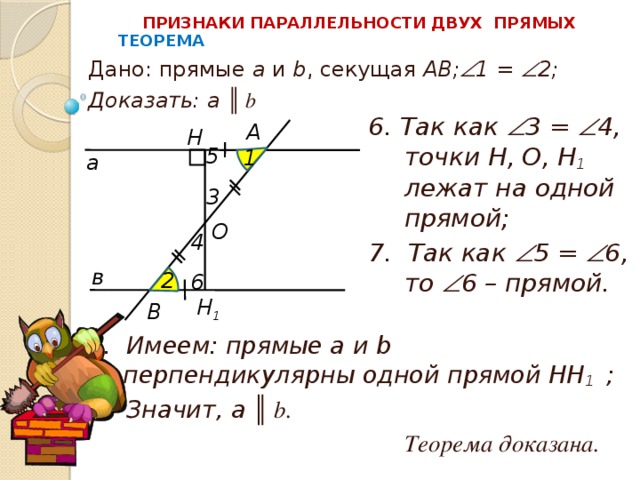
6. Так как 3 = 4, точки Н, О, Н 1 лежат на одной прямой;
7. Так как 5 = 6, то 6 – прямой.
А
H
5
1
а
3
O
4
в
2
6
H 1
В
8. Имеем: прямые а и b перпендикулярны одной прямой HH 1 ;
9. Значит, а ║ b.
Теорема доказана.


ВТОРОЙ ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
ТЕОРЕМА
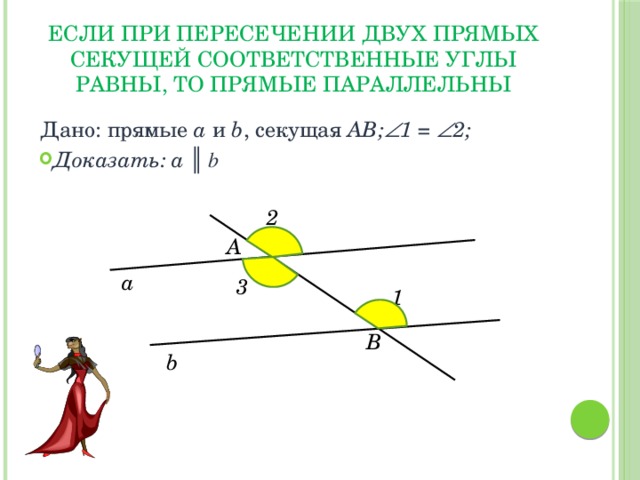
ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ СООТВЕТСТВЕННЫЕ УГЛЫ РАВНЫ, ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
Дано: прямые a и b , секущая АВ; 1 = 2;
2
А
а
3
1
В
b

ТРЕТИЙ ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
ТЕОРЕМА
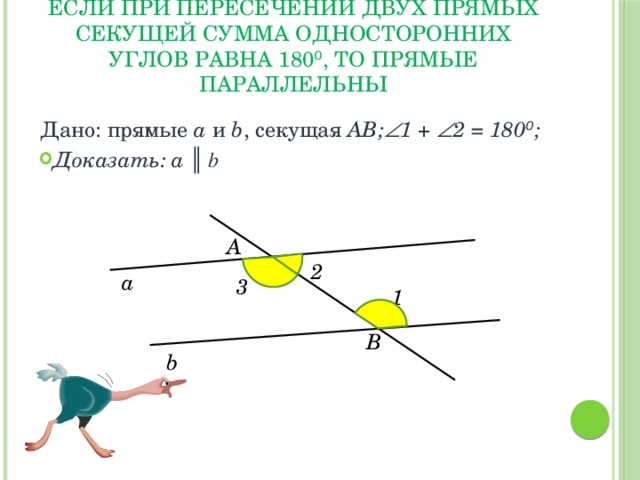
ЕСЛИ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ CУММА ОДНОСТОРОННИХ УГЛОВ РАВНА 180 ⁰ , ТО ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
Дано: прямые a и b , секущая АВ; 1 + 2 = 180 ⁰ ;
А
2
а
3
1
В
b
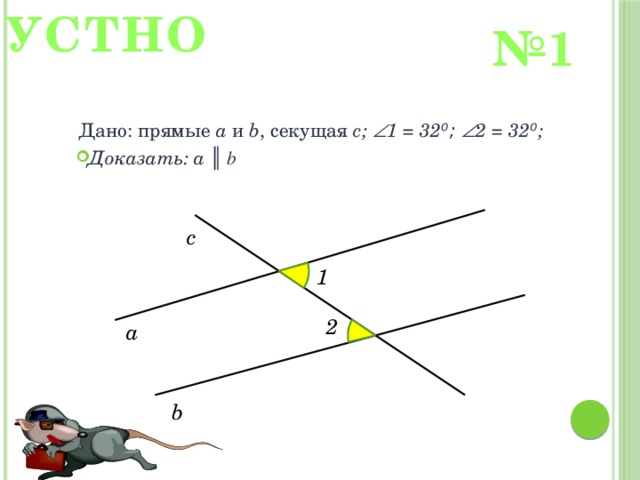
УСТНО
№ 1
Дано: прямые a и b , секущая с; 1 = 32 ⁰; 2 = 32 ⁰ ;
с
1
2
а
b
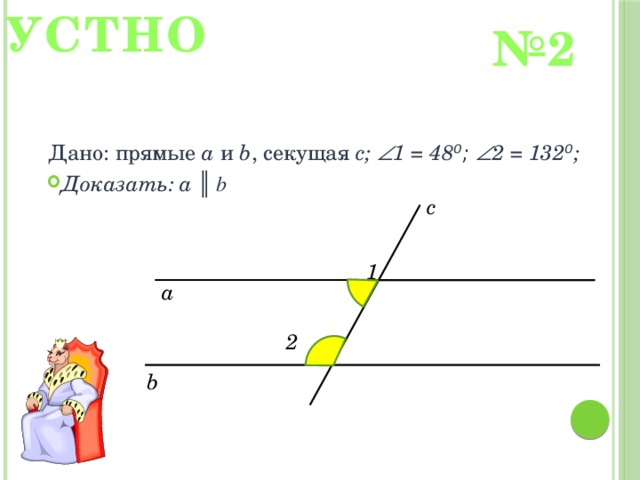
УСТНО
№ 2
Дано: прямые a и b , секущая с; 1 = 48 ⁰; 2 = 132 ⁰ ;
с
1
а
2
b
УСТНО
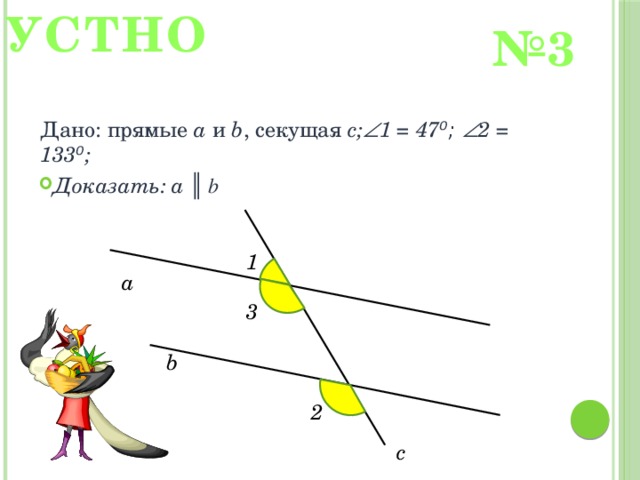
№ 3
Дано: прямые a и b , секущая с; 1 = 47 ⁰; 2 = 133 ⁰ ;
1
а
3
b
2
с
УСТНО
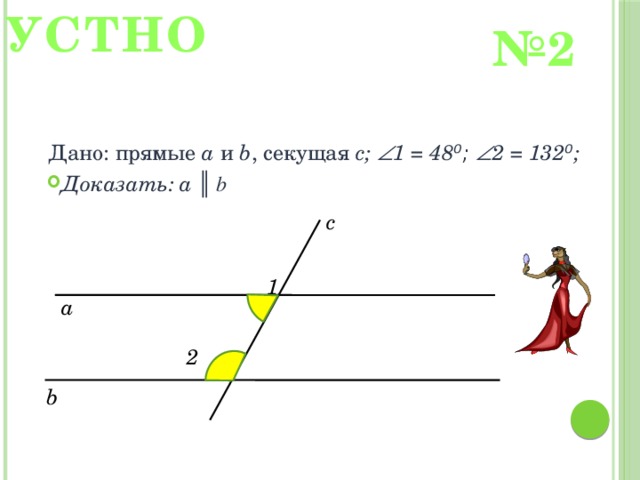
№ 2
Дано: прямые a и b , секущая с; 1 = 48 ⁰; 2 = 132 ⁰ ;
с
1
а
2
b
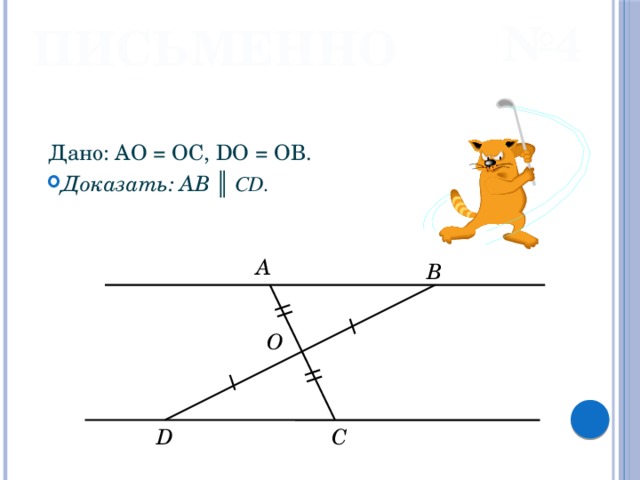
№ 4
ПИСЬМЕННО
Дано: AO = OC, DO = OB.
A
B
O
C
D
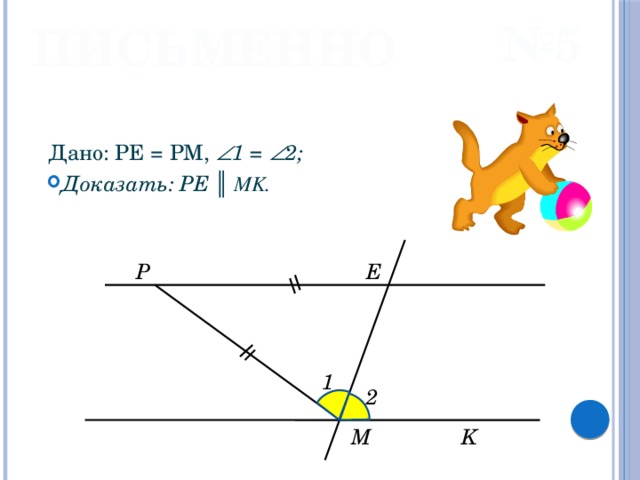
№ 5
ПИСЬМЕННО
Дано: PE = PM, 1 = 2;
E
P
1
2
M
K
№ 6
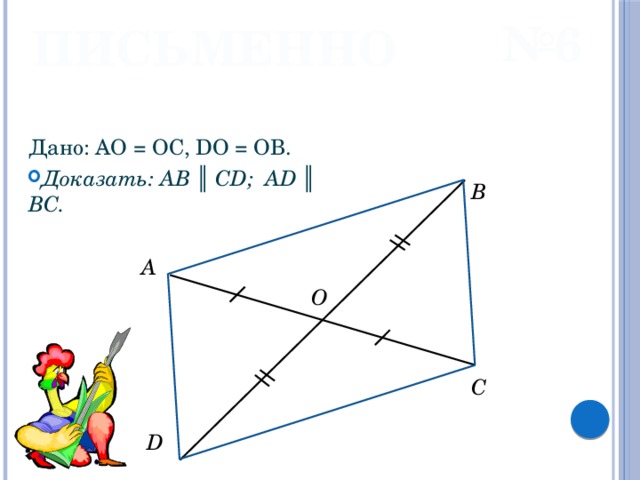
ПИСЬМЕННО
Дано: AO = OC, DO = OB.
- Доказать: AB ║ CD; AD ║ BC.
B
A
O
C
D
№ 7
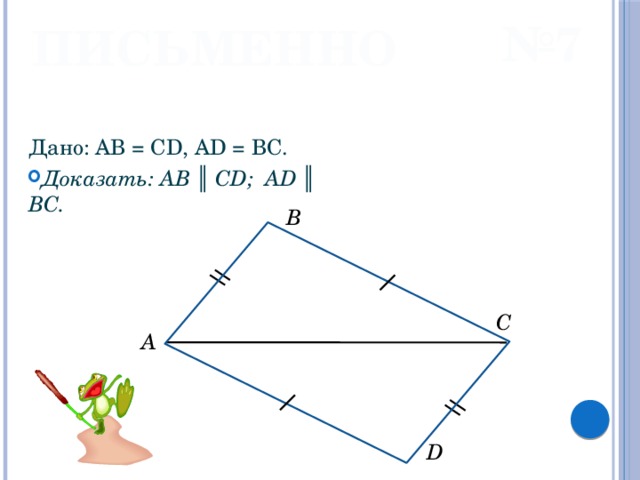
ПИСЬМЕННО
Дано: AB = CD, AD = BC.
- Доказать: AB ║ CD; AD ║ BC.
B
C
A
D


 Получите свидетельство
Получите свидетельство Вход
Вход























































 Признаки параллельности прямых (1.22 MB)
Признаки параллельности прямых (1.22 MB)
 0
0 3954
3954 205
205 Нравится
0
Нравится
0







