Презентация "Приёмы устного счёта"

МКОУ «Колпаковская СОШ»

«Устный счет - гимнастика ума»

Над проектом работали:

Ученицы МКОУ «Колпаковская СОШ»

Бабаева Д., Исмаилова Н.

Руководитель: Ежова Л.М.

2015г .

«Счет и вычисления – основы порядка в голове» Иоганн Генрих Песталоцци (1746 - 1827)

• Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Освоение вычислительных навыков развивается память и помогает усваивать предметы естественно-математического цикла.
• Мотивацией для выбора темы послужило желание продолжения формирования вычислительных навыков, умения быстро и чётко находить результат математических действий.

Изучить и научиться применять некоторые способы быстрого счета.

Путешествие по словарям

Толковый словарь русского языка. Владимир Даль: «Натуральные числа (арие) – природныя, порядковыя 1,2,3 и пр. – историi, ученье о трёх царствахъ природы, объ исковаемыхъ, растенияхъ, животныхъ»

Краткий справочник школьника. В.С. Крамор, В.А.Попов: «Числа, употребляемые для счёта предметов, называются натуральными »

Словарь русского языка С.И.Ожегов. Такого понятия нет. «Натуральный» – соответствующий природе вещей, подлинный, природный.

Википедия свободная энциклопедии. Натуральные числа (естественные числа) числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления). .

Ну-ка в сторону карандаши!

Ни костяшек. Ни ручек. Ни мела.

Устный счёт! Мы творим это дело

Только силой ума и души.

Числа сходятся где-то во тьме,

И глаза начинают светиться,

И кругом только умные лица,

Потому что считаем в уме.

Валентин Берестов (1928-1998)

Способ быстрого умножения чисел в пределах первого десятка на 9. Допустим, нам нужно умножить 7 на 9.

Повернём руки ладонями к себе и загнём седьмой палец (начиная считать от большого пальца слева).

Число пальцев слева от загнутого будет равно десяткам, а справа - единицам искомого произведения.

• Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:
• 53 х 11 = 583 Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8 Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583
• 59 х 11 = 649 Шаг 1 — 5 + 9 = 14 Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка) Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649

Умножение двузначных чисел на 11, 101

65*11=715

6 (6+5) 5

45*11=495

4 (4+5) 5

87*11=957 34*101=3434

8 (8+7) 7 57*101=5757

Задание: Умножьте быстро 54∙11

Проверь себя!

54∙11=594

Задание: Умножьте быстро 67∙11

Проверь себя!

67∙11=737

Признак делимости на 6

Число делится на 6, если оно делится одновременно и на 2 и на 3. В противном случае — не делится

Признак делимости чисел на 11

На 11 делятся только те натуральные числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места, или разность суммы цифр нечетных мест и суммы цифр четных мест кратна 11. Например: 105787 (1 + 5 + 8 = 14 и 0 + 7 + 7 = 14); 9 163 627 (9 + 6 + б + 7 = 28 и 1 + 3 + 2 = 6); 28 — 6 = 22; 22 : 11 = 2).

Существует и другой признак делимости на 11, удобный для не очень больших чисел.

Испытуемое число разби

вают слева на группы

по две цифры в каждой

и складывают эти группы.

Если полученная сумма

кратна 11, то испытуемое

число кратно 11.

Испытаем число

26741

Разбиваем на группы

2 | 67 | 41 и складываем их:

2+67+41=110

110 делится на 11 , значит,

и 26741 делится на 11 .

• Чтобы двузначное число умножить на 22, 33, ..., 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 44 = 4 11; 55 = 5 ∙ 11 и т.д. Затем произведение первых чисел умножить на 11.
• Пример 1. 24∙22=24∙2∙11=48∙11=528
• Пример 2. 23∙33=23∙3∙1=69∙11=759

Задание: Умножьте 18∙44

Проверь себя!

18∙44=18∙4∙11=72∙11=792

• Чтобы умножить какое-нибудь число, нужно данное число разделить 4.
• Ответ - полные сотни, остаток – неполные (1, 2, 3 или 25, 50, 75).
• Пример. 135 ∙ 25=(135:4=100:4+35:4)=33 сотни, остаток 3 (или неполная сотня – 75)=3375.

Задание: Умножьте быстро 126 ∙ 25

Проверь себя!

126:4=100:4+26:4= 31 сотня, остаток 2(или неполная сотня – 50)=3150

Чтобы возвести в квадрат: число десятков умножаем на

следующее число стоящее в натуральном ряду и приписываем 25

25 2 = 625

45 2 = 2025

(2*3) 25

6 25

(4*5) 25

20 25

Задание: возведите в квадрат число 105

Проверь себя!

=100 ∙10∙(10 +1) +25=11025

Возведение в квадрат чисел начинающихся на 5

К 5 2 прибавляем вторую цифру и приписываем квадрат второго числа, если он – однозначное число, то перед ним ставим ноль

52 2 =2704 58 2 =3364

(5 2 +2) 04 (5 2 +8) 64

27 04 33 64

Возведение в квадрат чисел:

11²=121

1 переписываем, 1 удваиваем и 1 возводим в квадрат

12²=144

1 переписываем, 2 удваиваем и 2 возводим в квадрат

13²=169

1 переписываем, 3 удваиваем и 3 возводим в квадрат

14²=196

1 переписываем, 4 удваиваем и 4 возводим в квадрат, т .к. 16 двузначное число, то 8 увеличиваем на 1, пишем 9 и приписываем 6

Деление на 25

Деление на 5

• На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5 Шаг1: 195×2 = 390 Шаг2: Переносим запятую: 39,0 или просто 39. 2978 / 5 Шаг1: 2978×2 = 5956 Шаг2: 595,6

• На 25 делятся нацело те

числа, которые оканчиваются на 25, 50, 75, 00.

• Например: 1209 75 ,4 50 ,

517460 25 , 6632013 00 .

Деление на 50

a : 50=a ∙ 2:100

Признак делимости на 8

Подобен признаку делимости на 4. Число делится на 8, если три последние цифры его нули или образуют число, делящееся на 8. В остальных случаях — не делится.

Примеры:

125 000 делится на 8 (три нуля в конце). 170 004 не делится на 8 (три последние цифры дают число 4, не делящееся на 8). 111 120 делится на 8 (три последние цифры дают число 120, делящееся на 8 ).

  11 ∙ 11 =121

111 ∙ 111 = 12321

1111 ∙ 1111 = 1234321

11111 ∙ 11111 =123454321

..........................

111111111 ∙ 111111111 = 12345678987654321

Картина Н.П. Богданова-Бельского «Устный счёт» была написана в 1895 г., то есть более 110 лет назад.

А какую же задачу дал им учитель? Не сможем ли решить ее и мы?

гимн учителю и ученику!

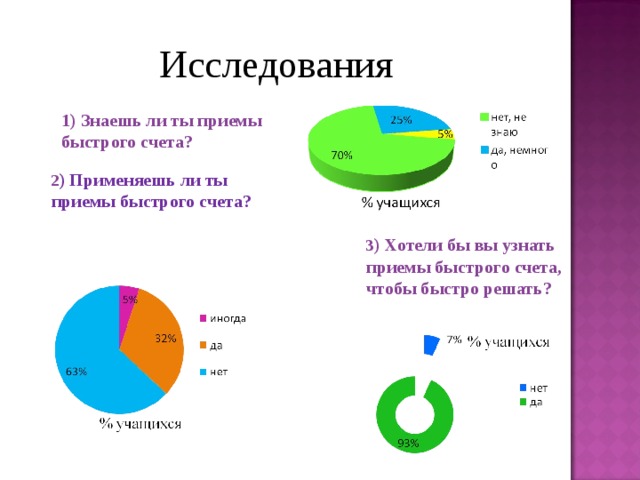
Исследования

1) Знаешь ли ты приемы быстрого счета?

2 ) Применяешь ли ты приемы быстрого счета?

3 ) Хотели бы вы узнать приемы быстрого счета, чтобы быстро решать?

3. Решите задачу.

Три поросенка Ниф-Ниф, Наф-Наф и Нуф-Нуф собрали в лесу 137 желудей. Удастся ли поросятам разделить желуди поровну?

А умеете ли, вы считать? Каждый, конечно ответит: «Да !»

• Арутюнян Е., Левитас Г. Занимательная математика.- М.: АСТ – ПРЕСС, 1999. – 368 с.
• Гарднер М. Математические чудеса и тайны. – М., 1978.
• Глейзер Г.И. История математики в школе. – М.,1981.
• «Первое сентября» Математика №3(15), 2007.
• Татарченко Т.Д. Способы быстрого счета на занятиях кружка, «Математика в школе», 2008, №7, стр.68
• Устный счет/Сост. П.М.Камаев. – М.: Чистые пруды, 2007- Библиотечка «Первого сентября», серия «Математика». Вып. 3(15).
• http://portfolio.1september.ru/subject.php