Презентация по математике "Сумма углов треугольника"

Презентация содержит в себе сведения из истории, теоретический  материал по теме,  задания для закрепления и первичного контроля знаний.

Выполните задание

Найти третий угол треугольника, если два остальные угла равны:

 30° и 40°

 20° и 80°

 120° и 40°

 90° и 45°

 60° и 60°

 150° и 30°

 100° и 70°

 80° и 80°

Сумма углов треугольника

Демонстрационный материал к уроку геометрии в 7 классе

Автор: Смирнова Елена Андреевна,

учитель математики МАОУ «Гимназия №87» г. Саратова

Сумма углов треугольника

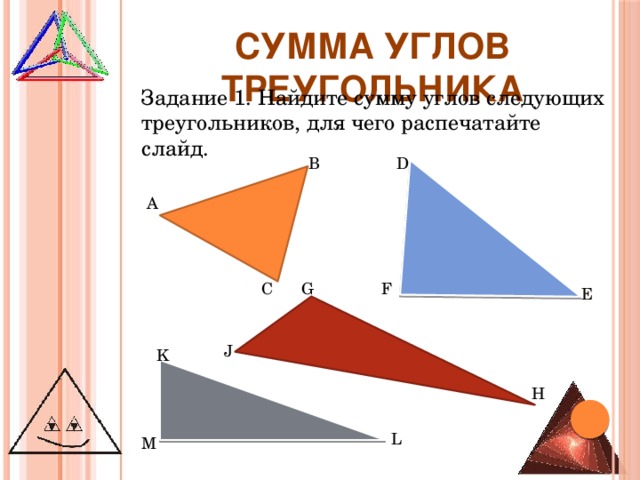
Задание 1. Найдите сумму углов следующих треугольников, для чего распечатайте слайд.

D

В

А

F

С

G

E

J

K

H

L

M

Сумма углов треугольника

Задание 2. Результаты исследований занесите в таблицу.

треугольник

Углы

1

2

3

Сумма

Сумма углов треугольника

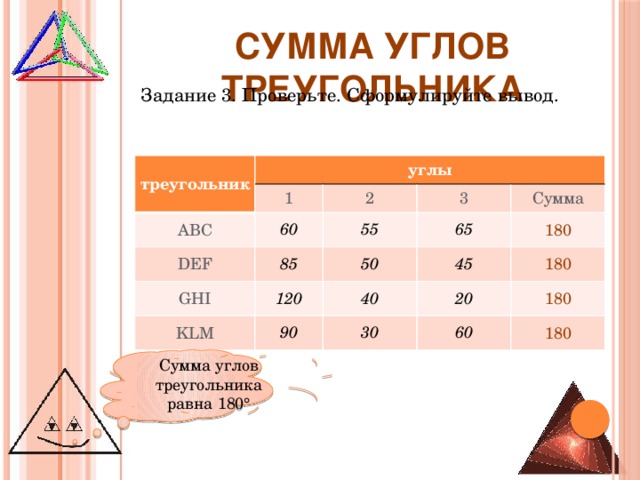
Задание 3. Проверьте. Сформулируйте вывод.

треугольник

углы

1

ABC

60

DEF

2

GHI

85

55

3

65

120

Сумма

50

KLM

90

40

180

45

20

180

30

180

60

180

Сумма углов треугольника равна 180 

Теорема 4.4 о сумме углов треугольника

Сумма углов треугольника равна 180°

Идея доказательства : свести к известной теореме, в которой фигурирует равенство угла 180°.

Сформулируйте эту теорему!...

Теорема о сумме углов треугольника

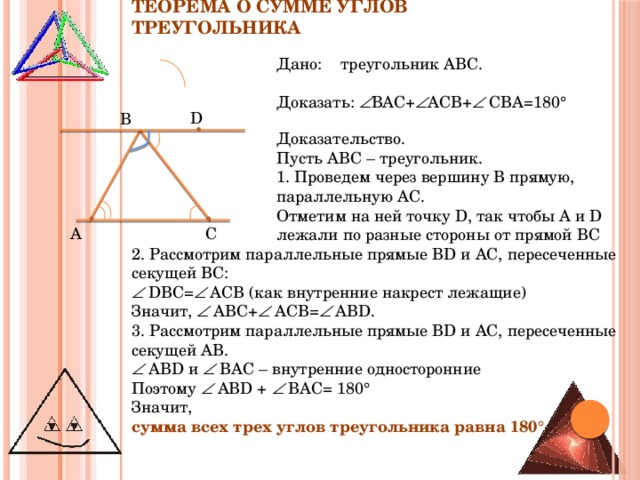
Дано: треугольник АВС.

Доказать:  ВАС+  АСВ+  СВА=180°

D

В

Доказательство.

Пусть АВС – треугольник.

1. Проведем через вершину В прямую, параллельную АС.

Отметим на ней точку D, так чтобы А и D лежали по разные стороны от прямой ВС

С

A

2. Рассмотрим параллельные прямые BD и AC, пересеченные секущей BC:

 DBC=  ACB (как внутренние накрест лежащие)

Значит,  ABC+  ACB=  АBD.

3. Рассмотрим параллельные прямые ВD и AC, пересеченные секущей АВ.

 АВD и  ВАС – внутренние односторонние

Поэтому  АВD +  ВАС= 180°

Значит,

сумма всех трех углов треугольника равна 180°

Выполните задание

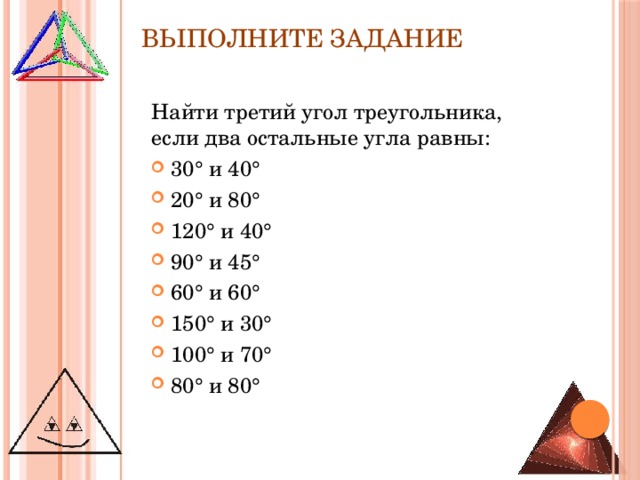
Найти третий угол треугольника, если два остальные угла равны:

• 30  и 40 
• 20  и 80 
• 120  и 40 
• 90  и 45 
• 60  и 60 
• 150  и 30 
• 100  и 70 
• 80  и 80 

Выполните задания

I вариант

II вариант

Построить треугольник, у которого:

а) все углы острые

б) два угла тупых,

а) два угла острых

в) все углы прямые

б) все углы тупые

в) два угла прямых

Все ли треугольники удалось построить?

Выполните задания

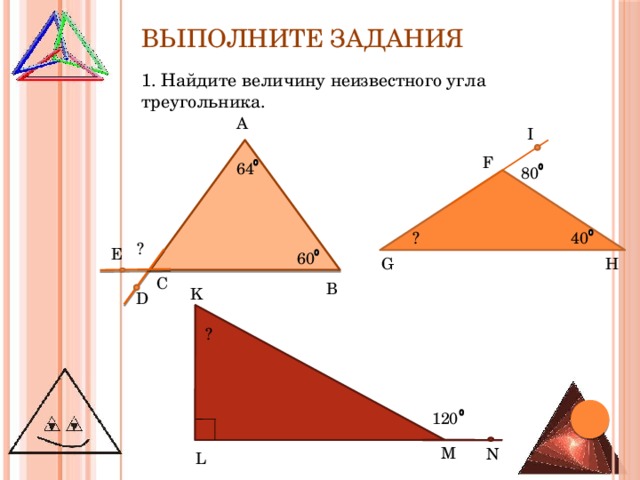
1. Найдите величину неизвестного угла треугольника.

А

I

F

64

80

40

?

?

E

60

H

G

С

В

K

D

?

120

M

N

L

Выполните задания

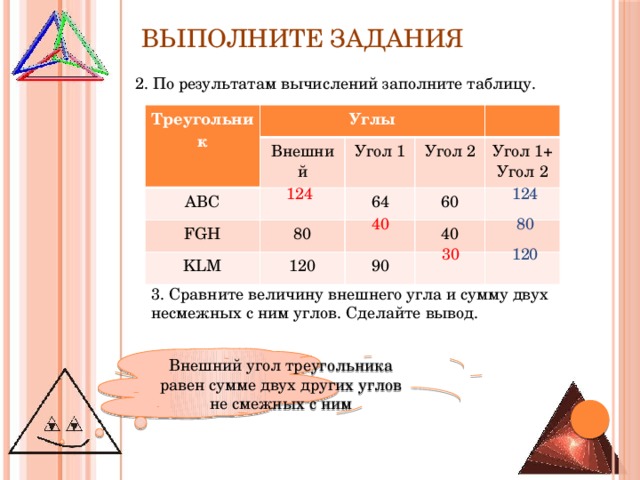
2. По результатам вычислений заполните таблицу.

Треугольник

Углы

Внешний

АВС

FGH

Угол 1

80

KLM

64

Угол 2

60

120

Угол 1+ Угол 2

40

90

124

124

80

40

120

30

3. Сравните величину внешнего угла и сумму двух

несмежных с ним углов. Сделайте вывод.

Внешний угол треугольника равен сумме двух других углов не смежных с ним

Следствия из теоремы о сумме углов треугольника

1. У любого треугольника хотя бы два угла острые.

2. Внешний угол треугольника равен сумме двух других углов не смежных с ним.

Подумайте, как это можно доказать!

Из истории геометрии

Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия – "землемерие" (от греческого "гео" – "земля" и "метрео" – "измеряю").

Древние землемеры выполняли геометрические построения, измеряли длины и площади; астрологи рассчитывали расположение небесных светил – все это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике .

Геродот,

(484 до н. э. — 425 до н. э.)

Из истории геометрии

Треугольник всегда имел широкое применение в практической жизни. Так, в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и других древних документах.

В древней Греции учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, в школе Пифагора и других; оно было затем полностью изложено в первой книге "Начал" Евклида.

Фалес,

(640/624 — 548/545 до н. э.)

Пифагор,

(570—490 гг. до н. э.)

Из истории геометрии

Среди "определений", которыми начинается эта книга, имеются и следующие: "Из трехсторонних фигур равносторонний треугольник есть фигура, имеющая три равные стороны, равнобедренный же – имеющая только две равные стороны, разносторонний – имеющая три неравные стороны". Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.

Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.