Модуль действительного числа, функция модуля

В презентации содержатся устные  задания на повторение вычисления модуля действительного числа, решения уравнений с модулем, основных графиков, известных учащимся.

Затем вводится  новая функция, определяются её свойства и построение графиков с использованием параллельного переноса.

После закрепления проводится обучающая самостоятельная работа.

Определение: модулем неотрицательного действительного числа х называют само это число; модулем отрицательного действительного числа х называют противоположное число.

Работа устно

• Вычислить:

Работа устно

• Вычислить:

Работа устно

• Решить уравнения:

Построение графика функции

у= |x+m|+t

Домашнее задание

№ 16.15

№ 16.16 (г)

№ 16.19

№ 16.36 (а)

Повторение теории

Определение : модулем неотрицательного действительного числа х называют само это число; модулем отрицательного действительного числа х называют противоположное число.

| x | - расстояние от 0 до х

Геометрический смысл модуля

x

5

-5

0

|5| = 5 , т.к. расстояние от 0 до 5 равно 5

| - 5| = 5 , т.к. расстояние от 0 до -5 равно 5

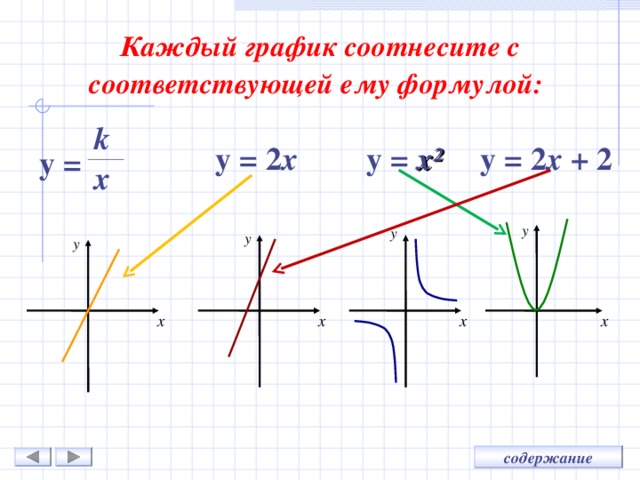
Каждый график соотнесите с соответствующей ему формулой:

k

y = 2 x + 2

y = 2 x

y = x²

y =

x

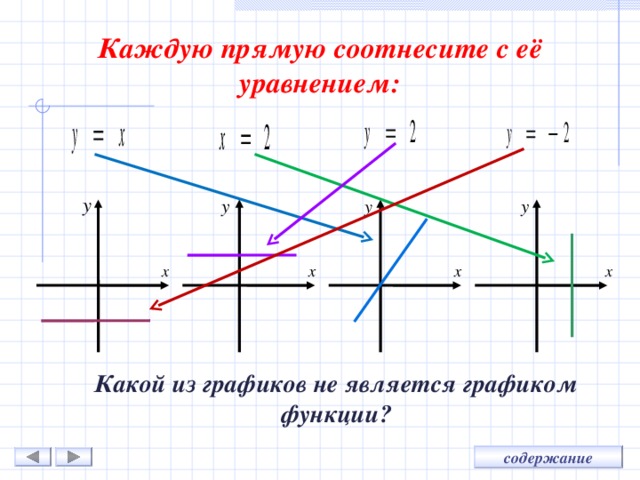
Каждую прямую соотнесите с её уравнением:

Какой из графиков не является графиком функции?

Повторение

формула

график

название

Прямая, 2 точки

Линейная

Парабола, 5 точек, в середине вершина

Квадратичная

Ветка параболы относительно оси Ох, 4 точки

Квадратный корень

Кубическая парабола

Степенная

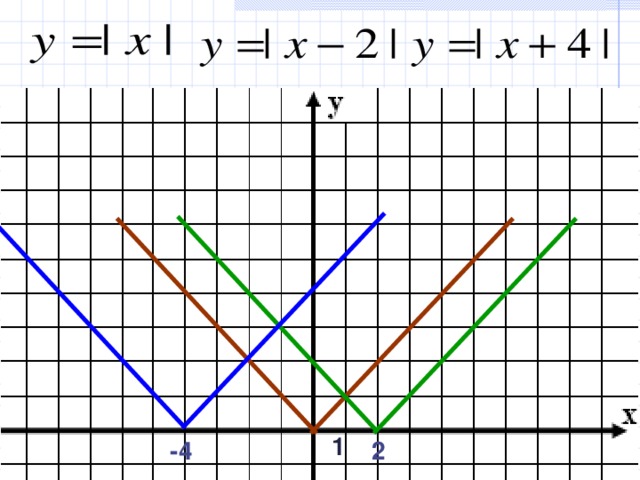
y = | х |

Модуль

«Галочка»

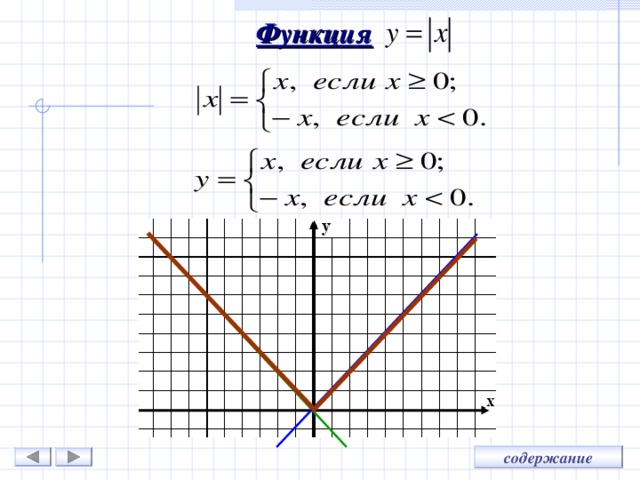
Функция

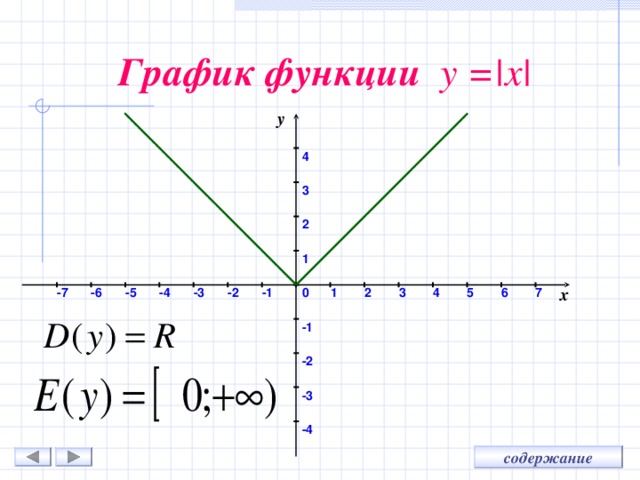
График функции у = |x|

y

4

3

2

1

x

5

6

4

7

3

2

-5

1

-1

-2

-3

-4

-6

-7

0

-1

-2

-3

-4

0 вправо , если m " width="640"

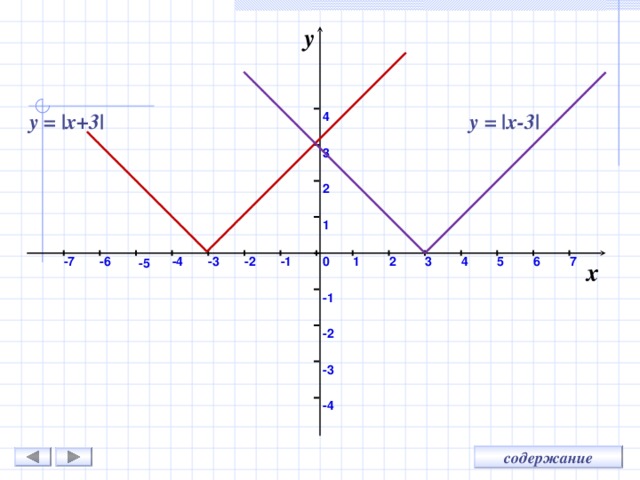
С помощью графика функции y = |x|

можно построить график функции

y = |x + m| методом движения вдоль оси Ох на m единиц:

влево , если m 0

вправо , если m

y

y = |x+ 3 |

y = |x-3|

4

3

2

1

-2

-3

7

0

6

5

4

-4

3

2

1

-7

-6

-1

-5

x

-1

-2

-3

-4

1

2

-4

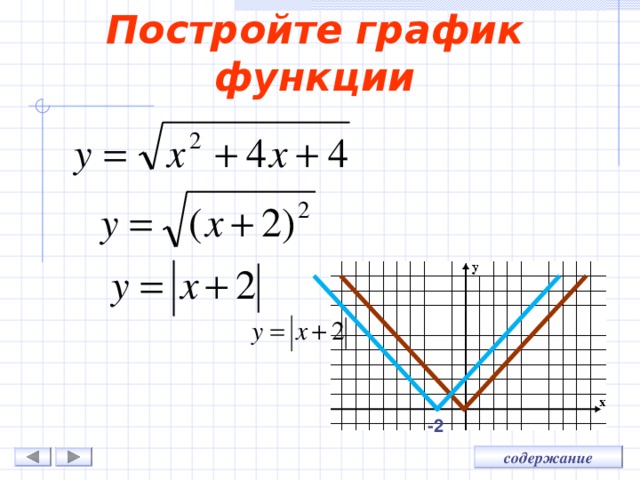
Постройте график функции

-2

0 вниз , если t " width="640"

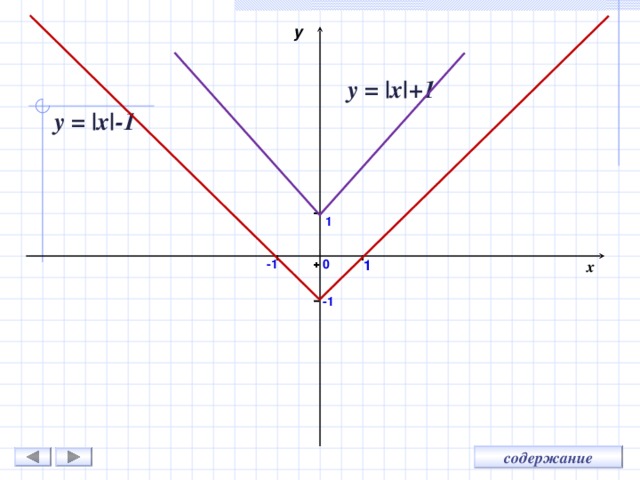
С помощью графика функции y = |x| можно построить график функции

y = |x|+t методом движения вдоль оси Оу на t единиц:

вверх , если t 0

вниз , если t

y

y = |x| + 1

y = |x| -1

1

-1

x

0

1

-1

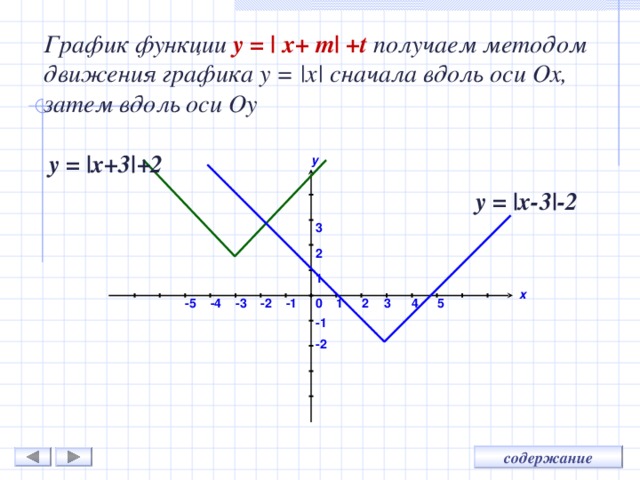
График функции y = | x+ m| +t получаем методом движения графика y = |x| сначала вдоль оси O х, затем вдоль оси O у

y = |x+3|+2

y

y = |x-3|-2

3

2

1

x

4

1

-2

2

-3

3

-1

-4

5

-5

0

-1

-2

у

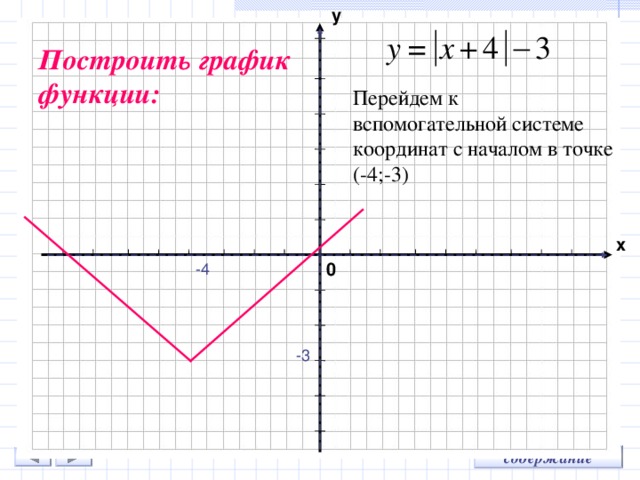
Построить график функции:

Перейдем к вспомогательной системе координат с началом в точке (-4;-3)

х

0

- 4

- 3

Самостоятельная работа

В самостоятельной работе 6 заданий . Вам необходимо определить каким уравнением задаётся график функции.

Найти его среди предложенных ответов.

Записать себе в тетрадь номер задания и вариант ответа.

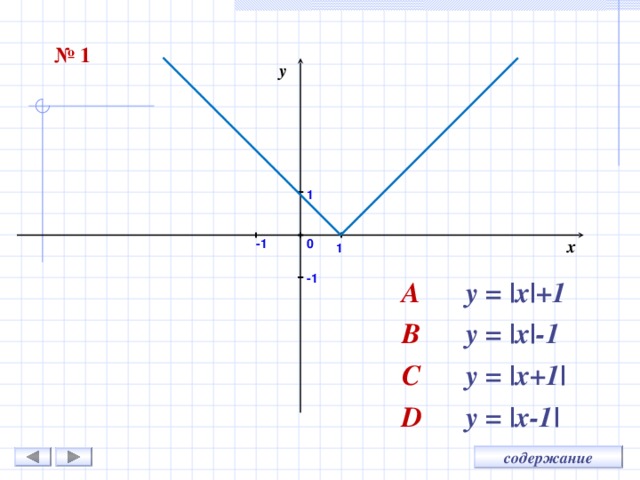
№ 1

y

1

x

0

-1

1

A y = |x|+1

B y = |x|-1

C y = |x+1|

D y = |x-1|

-1

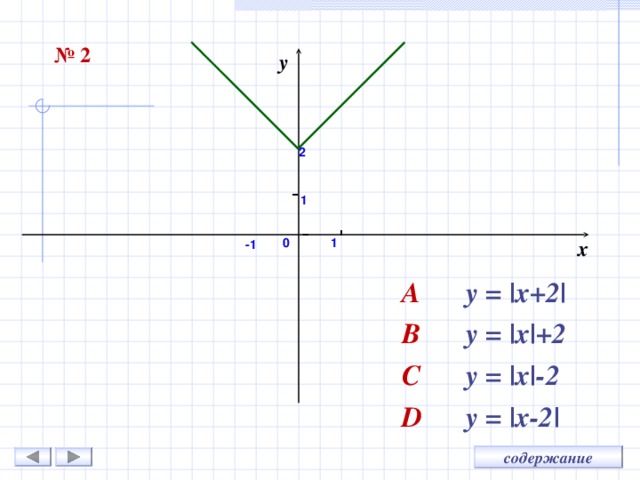
№ 2

y

2

1

0

x

1

-1

A y = |x+2|

B y = |x|+2

C y = |x|-2

D y = |x-2|

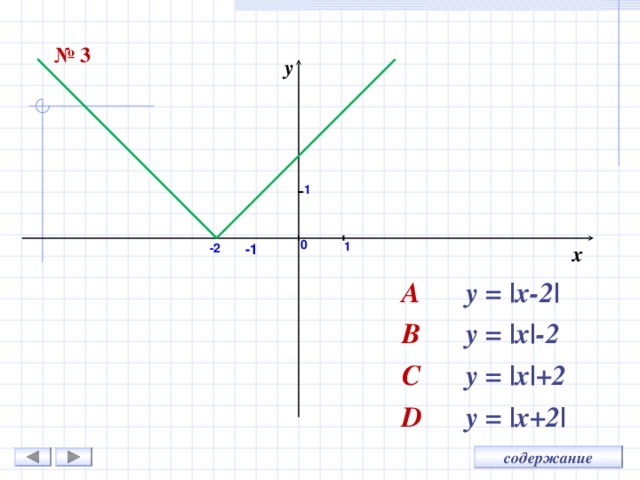
№ 3

y

1

0

1

x

-1

-2

A y = |x- 2 |

B y = |x|- 2

C y = |x|+ 2

D y = |x+ 2 |

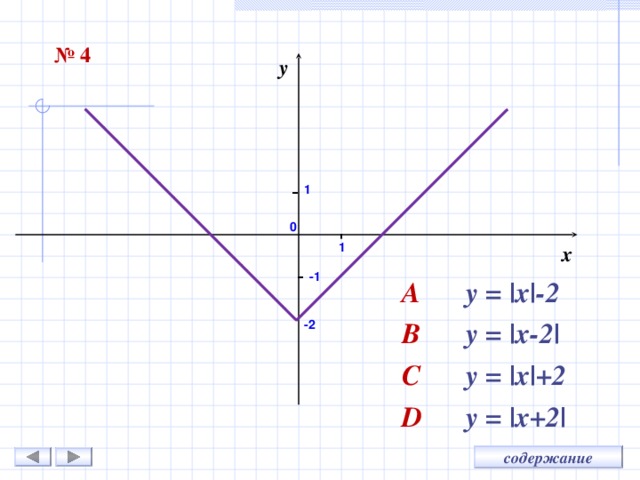
№ 4

y

1

0

1

x

-1

A y = |x|- 2

B y = |x- 2 |

C y = |x|+ 2

D y = |x+ 2 |

-2

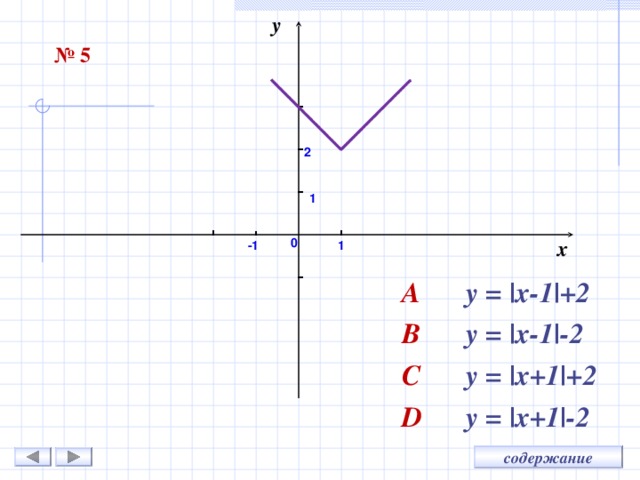
y

№ 5

2

1

0

x

-1

1

A y = |x -1 |+ 2

B y = |x -1 | - 2

C y = |x +1 |+ 2

D y = |x+ 1 |-2

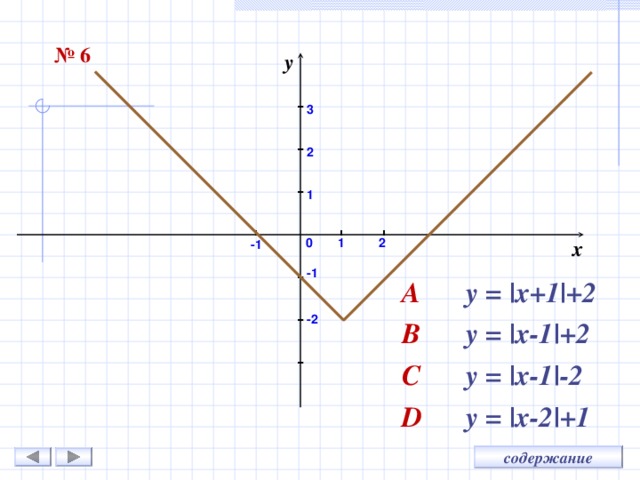
№ 6

y

3

2

1

0

1

2

x

-1

-1

A y = |x+1|+2

B y = |x-1|+2

C y = |x-1|-2

D y = |x-2|+1

-2

Проверьте свои ответы по ключу

• Задание 1 – D
• Задание 2 – B
• Задание 3 – D
• Задание 4 – A
• Задание 5 – A
• Задание 6 – С

Оценка самостоятельной работы

• Нет ошибок - 5 (пять) .
• Одна ошибка - 4 (четыре).
• Две ошибки - 3 (удовлетворительно)