Методическая разработка
Решение текстовых задач
с помощью графов
Содержание
Введение
Программа элективного курса
Примерный обобщающий тест
План урока на тему «Решение задач с помощью уравнений»
Заключение
Литература
Введение
Как известно, одной из центральных линий математической подготовки учащихся является линия «Уравнения», методы их решения, решение задач с помощью уравнений и систем уравнений.
Решения текстовых задач - это деятельность, сложная для учащихся. Сложность ее определяется, прежде всего, комплексным характером работы: нужно ввести переменную и суметь перевести условие на математический язык; соотнести полученный результат с условием задачи и, если нужно, найти значения еще каких-то величин. Каждый из этих этапов – самостоятельная и часто трудно достижимая для учащихся задача.
Данная программа составлена для работы с учащимися седьмых, восьмых, девятых классов, которые желают овладеть новым и эффективным способом решения текстовых задач на «движение», «стоимость», «совместную работу», «заполнение резервуара водой» и т. д.
Моделирование условия задачи с помощью сетевых графов позволяет ученику устанавливать различные связи и отношения между данными и искомыми величинами задачи, осознать идею решения, его логику, увидеть различные способы решения задачи, обосновывать выбор величин для введения переменных.
Составление графов становится для школьников увлекательным занятием и значительно повышает интерес к изучению темы курса алгебры «Решение задач с помощью уравнений». Деятельность учащихся приобретает более целенаправленный характер и, что самое важное, появляется самостоятельность на этапе поиска путей решения задачи, который, как известно, вызывает всегда большие затруднения.
Цель данной программы:
1) познакомить учащихся с новым способом решения текстовых задач - сетевым графом;
2) научить составлять уравнение по условию задачи, описывать выбор переменных уравнения; составлять и обосновывать выбор ответа.
Задачи:
Приобщить учащихся к работе с математической литературой.
Научить составлять математическую модель текстовой задачи, пере ходить от этой модели к ответам задачи, анализируя жизненную ситуацию текста задачи.
Программа предполагает знакомство учащихся с новым методом анализа и записи условия задачи, поиска пути составления уравнения. Включенный в курс материал может применяться для различных категории учащихся, так как он изложен понятным языком, простой формой записи схемы, обобщенностью и простотой алгоритма работы с текстом.
Контроль за степенью усвоения тем осуществляется уже при поэтапной работе по алгоритму, по построению сетевого графа, что позволяет установить степень достижения промежуточных результатов и итогового вывода – непосредственно уравнения, а также увидеть сбой в рассуждениях, в работе по алгоритму в любой момент процесса обучения.
Программа элективного курса
Вводное занятие
Осуществляется знакомство с алгоритмом анализа условия и построения сетевого графа; повторяются основные соотношения, используемые в задачах: S = vt, А = pt и т. п., поясняется суть терминов, используемых в алгоритме.
Тема: Решение арифметических задач
На примере арифметических задач «на движение», «работу», «стоимость» определяются основные приемы построения и работы с сетевым графом
Тема: Решение задач на составление уравнений
Рассматриваются алгебраические задачи на движение «в направлении», «по воде», «на совместную работу», «заполнение резервуара водой», «покупку» и т.п.
| №п/п | Название занятий | Количество часов |
| 1 | Вводное занятие: что такое граф | 1 |
| 2 | Решение арифметических задач | 2 |
|
| Решение задач на составление уравнений: |
|
| 3 | «На движение» | 3 |
| 4 | «На совместную работу» | 2 |
| 5 | Различных алгебраических задач (на стоимость и т.д.) | 1 |
| 6 | «Круглый стол» (зачет) | 0,5 |
Курс предназначен для учащихся 7-х, 8-х и 9-х классов, рассчитан на 8,5 часов аудиторного времени. Курс призван помочь учащемуся в овладении навыком решения задач с помощью уравнений и систем уравнений, повысить уровень общей математической культуры, оценить свой потенциал для дальнейшего обучения в профильной школе.
Учащиеся будут уметь:
1. Анализировать условие текстовой задачи, выявлять главное в тексте.
Обосновывать выбор переменной при составлении уравнения.
Решать полученные уравнения рациональным способом.
Знать:
1. Соотношения; показывающие связь между элементами в задачах на «движение», «работу».
2. Ориентировочные основы поиска путей решения задачи.
Для того чтобы научиться решать задачи, надо разобраться в том, как они устроены, из каких частей они состоят, каковы инструменты, с помощью которых проводится решение задач.
Любая задача представляет собой требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче. поэтому, приступая к решению какой-либо задачи, надо ее внимательно изучить, установить, в чем состоят ее требования (вопросы), каковы условия, исходя из которых надо решать задачу. Результаты предварительного анализа задачи надо как-то зафиксировать, записать. Схематическая запись задачи должна быть удобна, компактна и в то же время достаточно наглядна. Первой отличительной особенностью схематичной записи задач является широкое использование в ней разного рода обозначений, символов, букв, рисунков, чертежей и т.д. Второй особенностью является то, что в ней четко выделены все условия и требования задачи, а в записи каждого условия указаны объекты и их характеристики, наконец, в схематичной записи фиксируется лишь то, что необходимо для решения задачи, все другие подробности отбрасываются. Эти положения соблюдены в сетевых графах.
Чтобы обеспечить возможность решать задачу с необходимыми объяснениями и в определенной последовательности, дается список указаний. Этот список предлагается или в готовом виде, или составляется вместе с классом:
О каком процессе идет речь в задаче?
Какие величины характеризуют этот процесс?
Каким соотношением связаны эти величины?
Сколько различных процессов описывается в этой задаче?
Есть ли связь между элементами?
Отвечая на эти вопросы (вопросник этот висит на стенде в кабинете, записан на закладках или обложках тетрадей учащихся), ученики анализируют условие задачи, записывают его схематично. Эта схема - сетевой граф. Осталось добавить; что таким способом можно решать текстовую задачу, величины которой связаны соотношением А = В х С, т. е. задачи, которые решаются учащимися с трудом: задачи на движение, на совместную работу, заполнение резервуара водой и т.п.
Задача №1
Расстояние между деревнями Ельня и Сосновка равно 30 км. Изобразите дорогу между этими деревнями в виде шкалы, деления которой обозначают 3 км. Покажите на этой шкале, где окажется через 1час, через 2 часа после выхода пешеход, идущий из Ельни в Сосновку со скоростью 6 км/ч. Покажите, где он окажется через 3 часа после выхода, через 4 часа, через 5 часов?
При ответе на поставленные вопросы получается удобным повторение следующих моментов:
расстояние между двумя пунктами удобнее всего изображать в виде отрезка, само же расстояние, как число, есть длина этого отрезка;
Что такое скорость? Скорость движения - это· расстояние, которое проходит человек за единицу времени (1 ч, 1 мин и т. п.). Есть общепринятые обозначения терминов – расстояние (пройденный путь), скорость движения, время: S, ν, t.
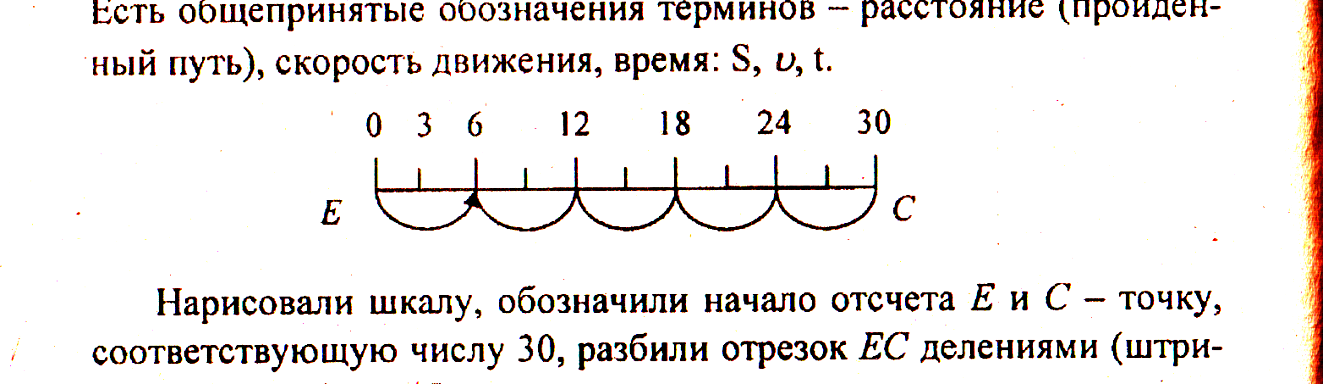
Нарисовали шкалу, обозначили начало отсчета Е и С - точку, соответствующую числу 30, разбили отрезок ЕС делениями (штрихами) ценой 3 км. Говоря о движении, мы имеем ввиду, что три величины характеризуют этот процесс: путь S, скорость ν, время t. Где был пешеход через 1 час после выхода? Это расстояние, которое прошел пешеход за 1 час, или скорость движения пешехода. Последний вопрос: где оказался пешеход через 5 ч? Делаем вывод: чтобы найти путь S, надо скорость движения умножить на время нахождения в пути. Записываем формулу S = ν·t, повторяем, как найти скорость, зная расстояние и время движения, как найти время, зная расстояние и скорость движения.
Задача №2
Машина прошла первый участок пути за 3 ч, а второй участок за 2 ч. Длина обоих участков вместе 267 км. С какой скоростью шла машина на каждом участке, если скорость на втором участке была на 8,5 км/ч больше, чем на первом?
Построим сетевой граф. Для применения уже выработанного алгоритма решения задачи нет выполнения условия – по ребру сетевого графа два незаштрихованных кружочка.
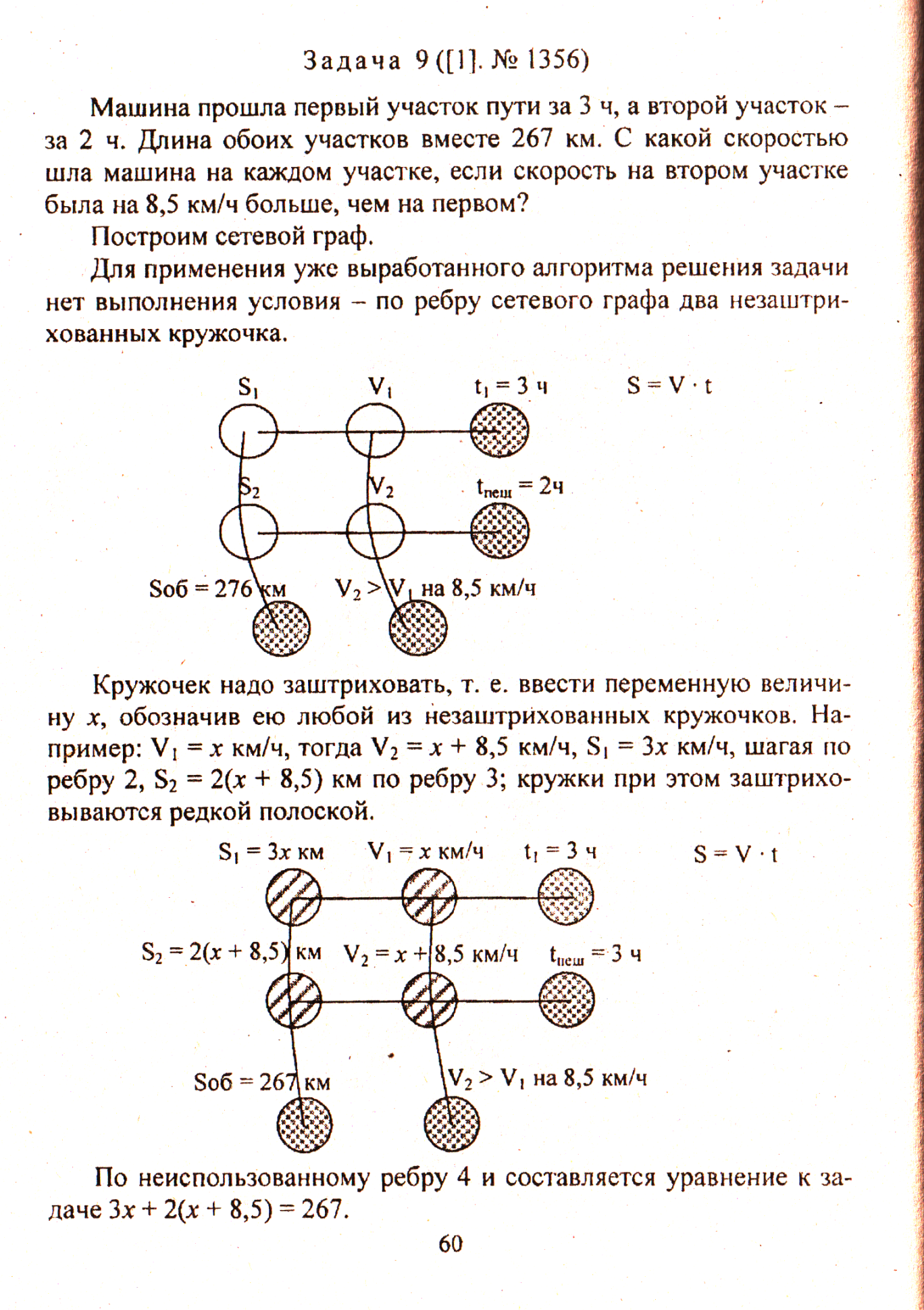
Кружочек надо заштриховать, т. е. ввести переменную величину х, обозначив ею любой из незаштрихованных кружочков. Например: ν1 = х км/ч, тогда ν2 = х + 8,5 км/ч, S1 = 3х км/ч, шагая по ребру 2, S2 = 2(х + 8,5) км по ребру 3; кружки при этом заштриховываются редкой полоской.
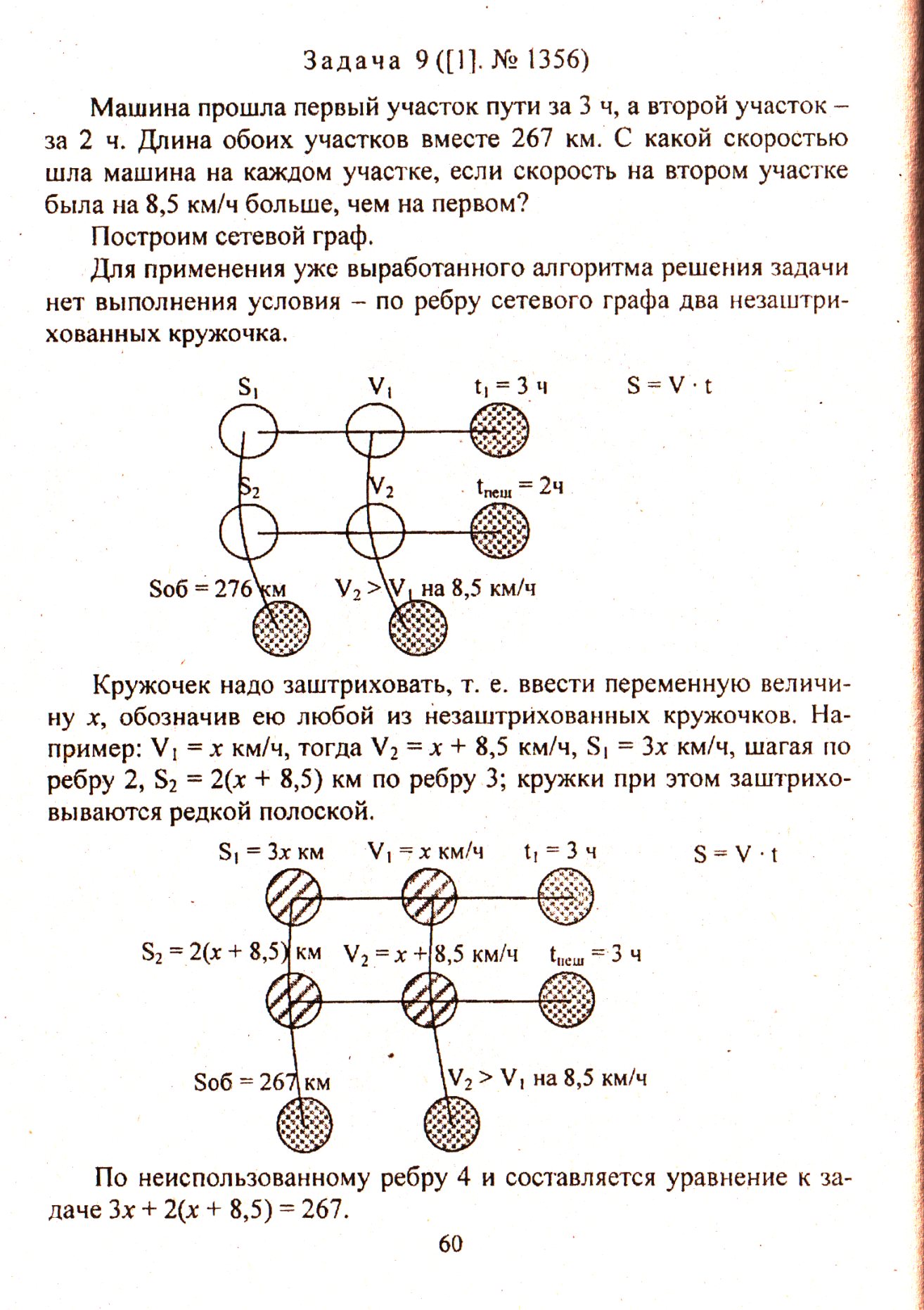
По неиспользованному ребру 4 и составляется уравнение к задаче
3х + 2(х + 8,5) = 267
Используя сетевой граф, уже легко объяснить (описать) составление уравнения по условию задачи, и слово «пусть» никого пугать не будет. Пусть на первом участке пути машина шла со скоростью х км/ч, тогда на втором участке скорость была (х + 8,5) км/ч. За 3 ч машина прошла 3х км, за 2 ч - 2(х + 8,5) км. Длина всего пути 267 км или 3х + 2(х + 8,5) км. Составим уравнение: 3х + 2(х + 8,5) = 267.
На первых порах естественным будет при записи объяснения пройтись еще раз по сетевому графу в той последовательности, в которой заштриховывались кружки.
Задача №3
Автобус шел 2 ч со скоростью 45 км/ч и 3 ч со скоростью 60 км/ч. Какой путь прошел автобус за эти 5 ч?
Все записи на сетевом графе делаются простым карандашом от руки, можно использовать ластик для корректирования. В левом столбце предлагаемой ниже таблицы описываются действия учителя и учащихся (вопросы, ответы, комментарии), в правой – сетевой граф, который параллельно вычерчивается на доске и в тетрадях:
О каком процессе идет речь в задаче? |
|
Какие величины характеризуют этот процесс? | 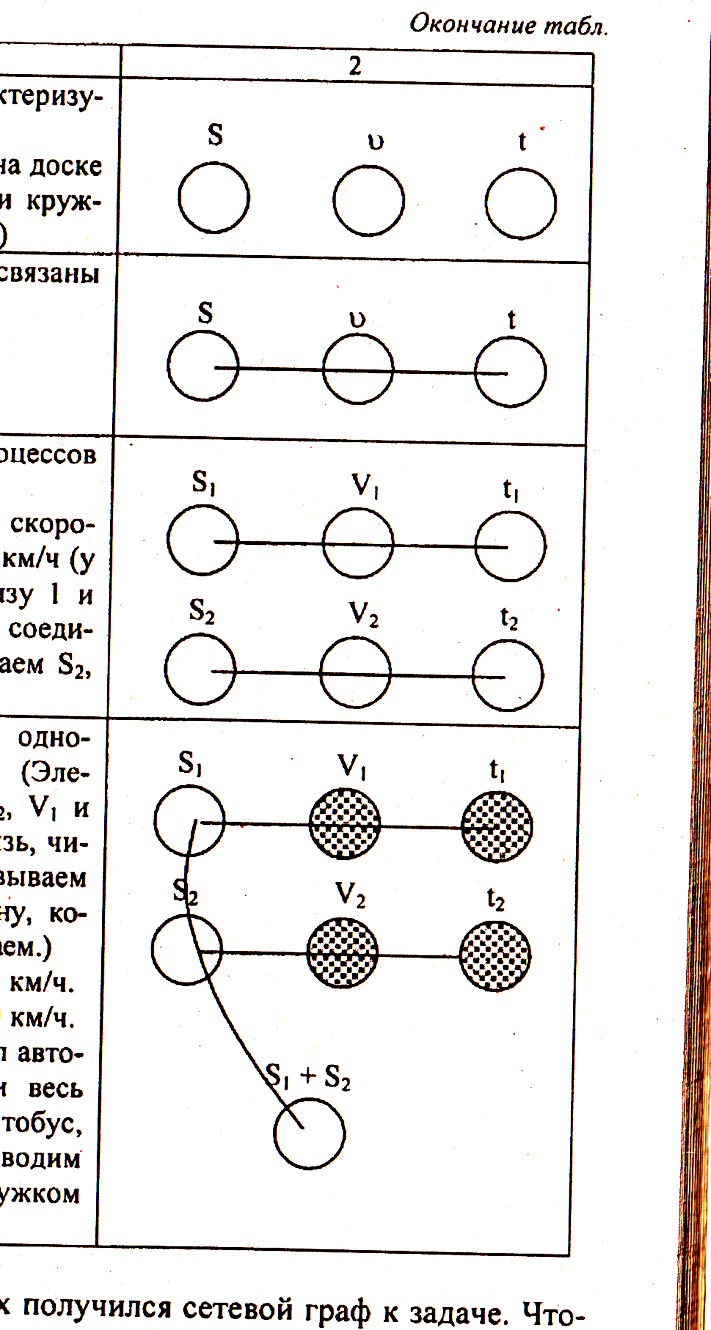
|
Каким соотношением связаны величины? S = ν·t | 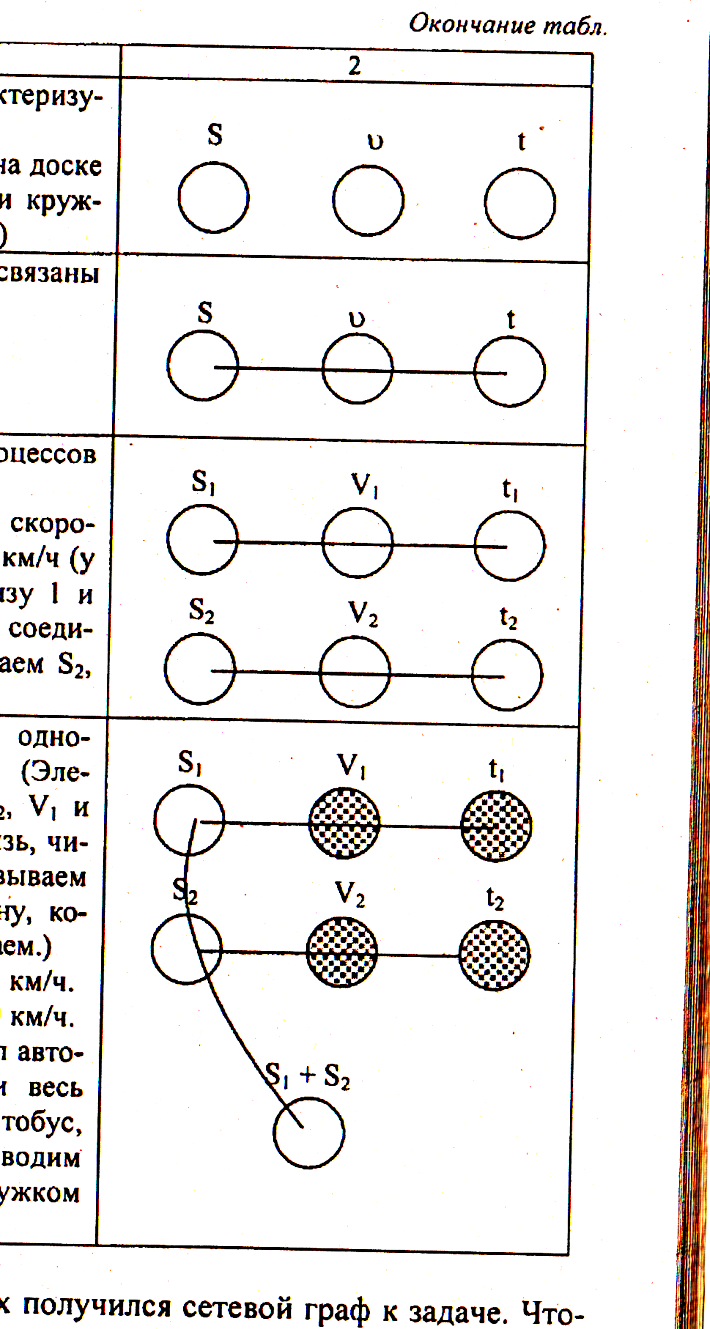
|
Сколько различных процессов описывается в задаче? Два: одно движение со скоростью 45 км/ч, второе – 60 км/ч (у букв S, ν и t ставим внизу 1 и рисуем ещё три кружка, соединяя их линией, и обозначим S2, ν2,·t2) | 
|
Есть ли связь между одноименными элементами? (Элементами являются S1 и S2, ν1 и ν2,·t1 и·t2. Отыскивая связь, читая условие; заштриховываем сплошным кружок величину, которая известна, и подписываем.) Два часа со скоростью 45 км/ч. Три часа со скоростью 60 км/ч. Какое расстояние прошел автобус за 5 ч? ( Надо найти весь путь, который прошел автобус, поэтому через S1 и S2 проводим линию и завершаем ее кружком S1+S2.) | 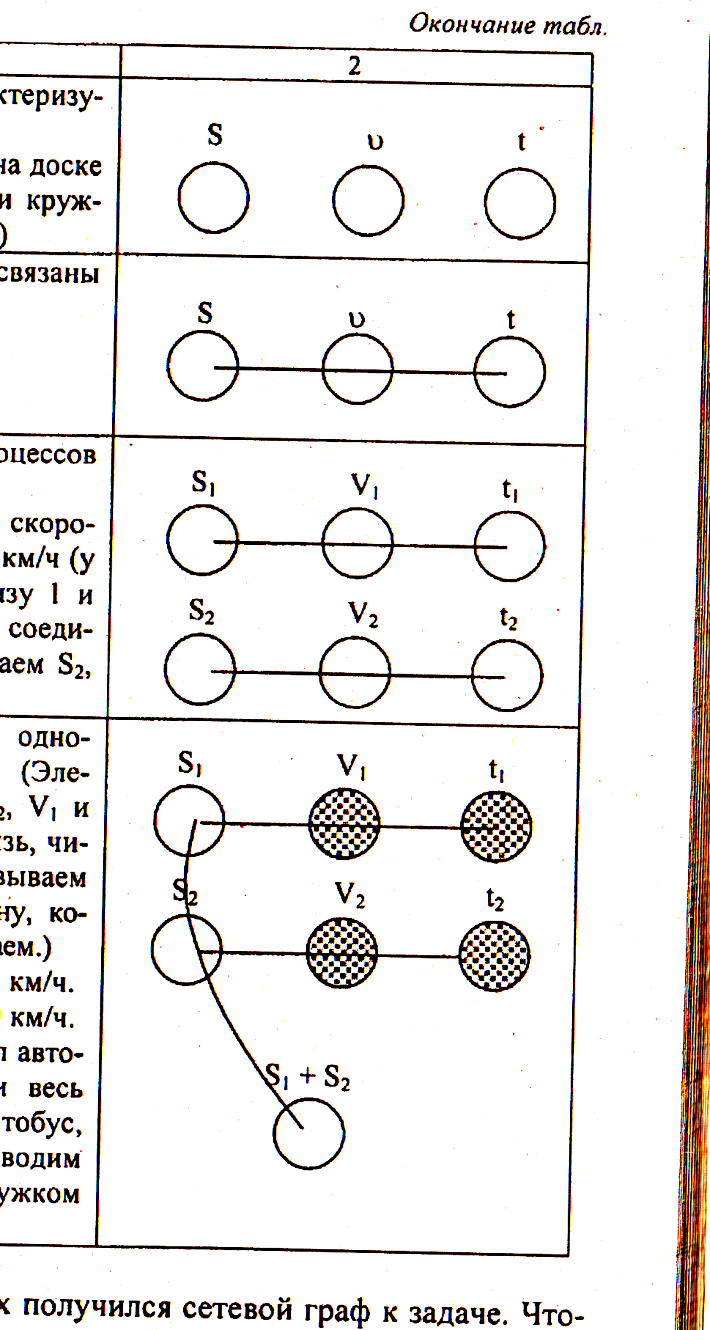
|
На доске и в тетрадях получился сетевой граф к задаче. Чтобы решить задачу, надо заштриховать все кружки. Каждая линия, а их три, называется ребром. Принцип заполнения (штриховки) кружков: зная (имея) два заштрихованных кружка на одном ребре, найти (заштриховать) третий. Те кружки, которые мы заполняем, решая задачу, штрихуются редкой полоской от руки.
Поясняем: первое ребро – , ν1 = 45 км/ч, t1= 2 ч. Можно найти S,? Можно обратиться к формуле, записанной правее: S1= 45·2 = 90 (км) И заштриховать кружок Sl; перечеркиваем использованное ребро. Аналогично второе ребро и величина S2. Остается третье, «вертикальное» ребро, в котором уже заштрихованы два кружка SI и S2, И значит, можно заштриховывать кружок SI + S2. Рассуждая так, параллельно ведется запись решения задачи с обязательным пояснением к каждому действию. Теперь работа ученика выглядит так:

45 х 2 = 90 (км) - прошел автобус за 2 ч.
60 х 3 = 180 (км) - прошел автобус за 3 ч.
90 + 180 = 270 (км) - прошел автобус за 5 ч.
Ответ: 270 км.
В учебнике есть аналогичные задачи, можно рассмотреть такую же в классе и задать на дом. Считаю обязательным проверить сетевой граф на следующем уроке с помощью кодоскопа, устно проpaботав его, или вызвав желающего к доске. дать ему возможность начертить сетевой граф, отвечая на вопросы.
Задача №4
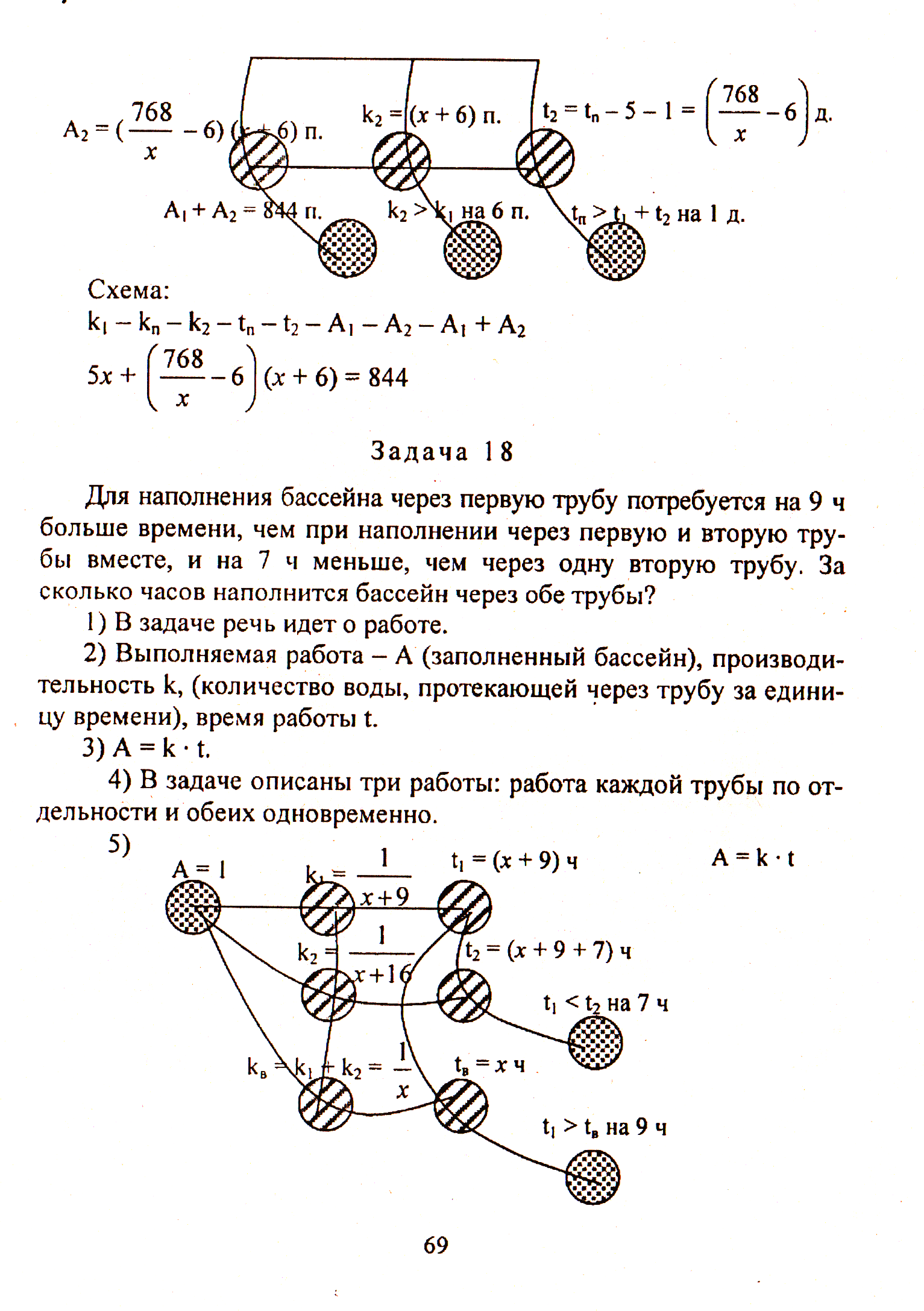
Бригада рабочих должна была за определенный срок изготовить 768 пылесосов. Первые пять дней бригада выполняла ежедневно установленную норму, а затем каждый день изготовляла на 6 пылесосов больше, чем намечалось, поэтому уже за день до срока было изготовлено 844 пылесоса. Сколько пылесосов в день должна была изготовлять бригада по плану?
В задаче .идет речь о работе.
Выполненная работа – А, производительность k и время работы t.
А = k·t.
В задаче описаны три вида работы: работа по плану, а фактическая работа состоит из двух «частей» - первые 5 дней с прежней производительностью и остальная часть работы с увеличенной производительностью.
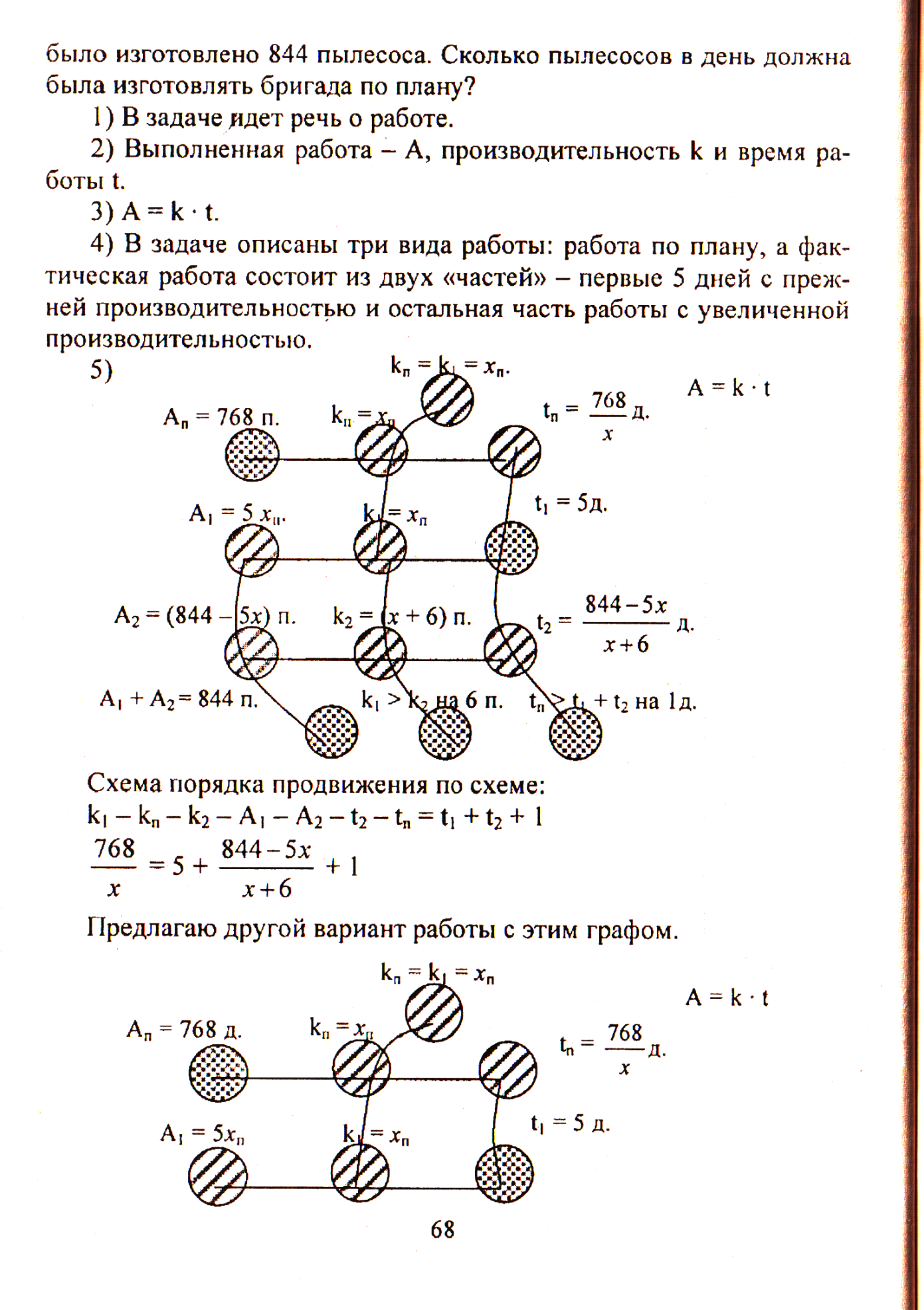
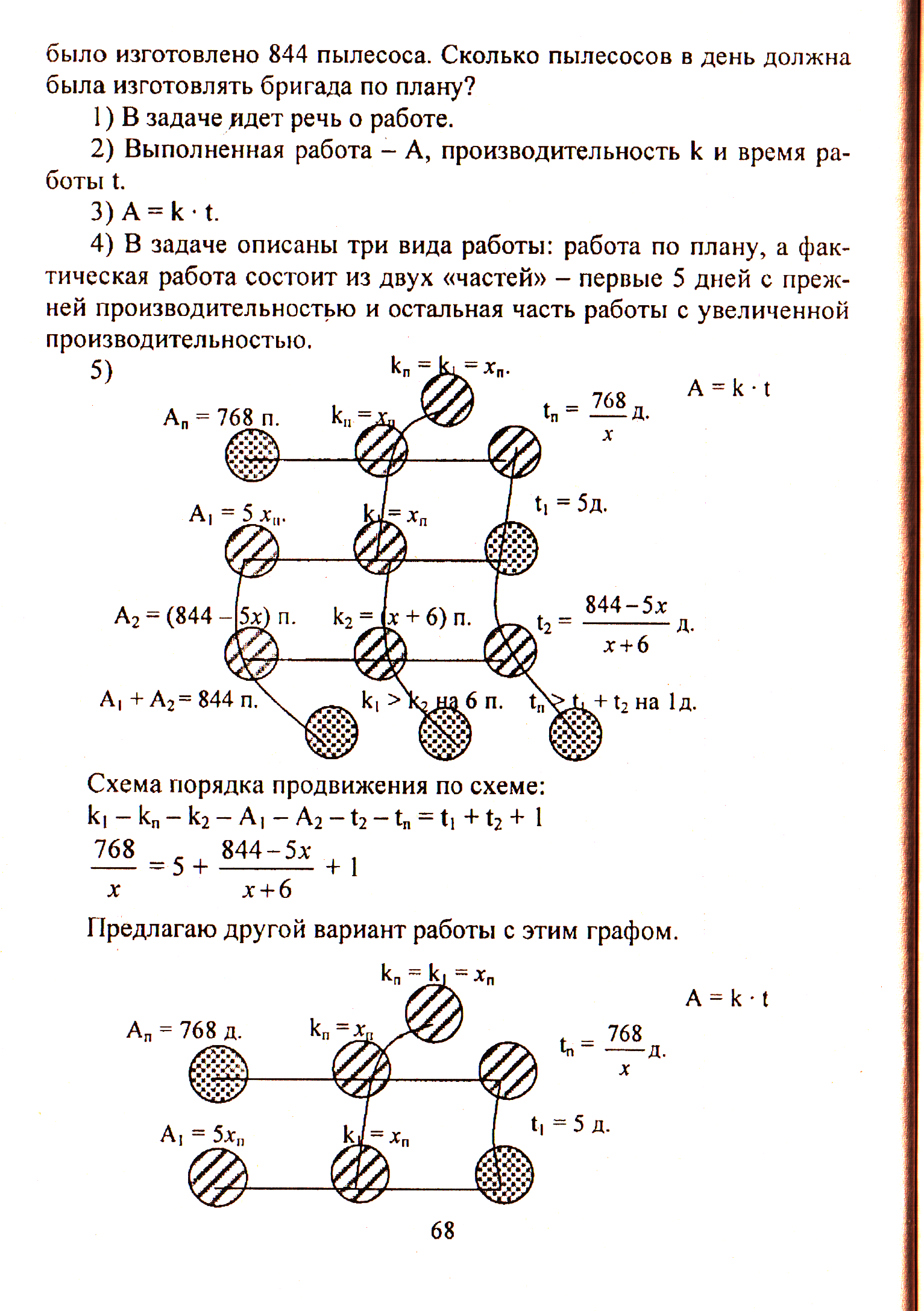
Задача №5
Для наполнения бассейна через первую трубу потребуется на 9 ч больше времени, чем при наполнении через первую и вторую трубы вместе, и на 7 ч меньше, чем через одну вторую трубу. За сколько часов наполнится бассейн через обе трубы?
В задаче речь идет о работе.
Выполняемая работа - А (заполненный бассейн), про изводительность k, (количество воды, протекающей ,через трубу за единицу времени), время работы t.
А = k·t.
В задаче описаны три работы: работа каждой трубы по отдельности и обеих одновременно.

tB-t1-k1-t2-k2-k1-kB=k1+k2
Получили уравнение: �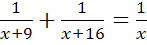 �.
�.
Задача №6
Два экскаватора, работая одновременно, выполняют некоторый объем земляных работ за 3 ч 45 мин. Один экскаватор, работая отдельно, сможет выполнить этот объем работ на 4 ч быстрее, чем другой. Сколько времени требуется каждому экскаватору в отдельности для выполнения того же объема земляных работ?
Здесь пригодится тот вопросник, который был по казан в начале работы:
О каком процессе идет речь в задаче? - О работе.
Какие величины характеризуют этот процесс? - Работа, производительность, время.
Каким соотношением связаны эти величины? - А = k · t.
Сколько различных процессов описывается в задаче? - Два: работы двух экскаваторов в отдельности и их совместная работа.
Есть ли связь между одноименными элементами? - Да, это связь между временем выполнения работы первого и второго экскаватора.
Сетевой график в данном случае будет выглядеть так

Уравнение к задаче составляем по нижнему, «горизонтальному» ребру графа:
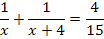
Его решением будут числа 6 и -2,5, последнее из которых отбрасываем ввиду того, что время – величина положительная.
Время, за которое второй экскаватор выполнит этот же объем работ, равно 10 ч.
Ответ: 6 ч, 10 ч.
| Бланк ответов к обобщающему тесту |
| Ф.И.О.______________ __________________ | Вариант ____________ |
| 1 | 2 | 3 | 4 |
|
|
|
|
|
Примерный обобщающий тест
Ответами на задания теста должно быть целое число или десятичная дробь, которые необходимо занести в бланк ответов:
| ВАРИАНТ 1 Николай и Андрей живут в одном доме. Николай вышел из дома и направился к школе. Через 4 мин после него из дома вышел Андрей и догнал своего друга у школы. Найдите расстояние от дома до школы, если Николай шел со скоростью 60 м/мин, а скорость Андрея 80 м/мин Из города А в город В, расстояние между которыми равно 300 км, выехал автобус. Через 20 мин навстречу ему из В в А выехал автомобиль и через 2 ч после выезда встретил автобус. С какой скоростью ехал автомобиль, если известно, что она была на 20 км/ч больше скорости автобуса? Мастерская получила заказ сшить 60 одинаковых халатов к определенному сроку. Ежедневно в мастерской шили на 2 халата больше, чем требовалось для выполнения заказа в срок, поэтому уже за 4 дня до срока осталось сшить 4 халата. Сколько халатов в день шили в мастерской? Лесхоз планировал заготовить за несколько дней 216 новогодних елей. Первые три дня лесхоз выполнял установленную ежедневную норму, а потом стал заготавливать на 2 ели в день больше. Поэтому уже за 1 день до срока было заготовлено 232 ели. Сколько елей ежедневно заготавливал лесхоз в первые три дня работы? | ВАРИАНТ 2 Мотоцикл, движущийся по шоссе со скоростью 60 км/ч, миновал пост ДПС. Через час мимо этого поста проехал автомобиль со скоростью 90 км/ч. На каком расстоянии от поста ДПС автомобиль догнал мотоцикл, если оба они ехали без остановок? Из города А в город В, расстояние между которыми 205 км, выехал автобус. Через 15 мин навстречу ему из В в А выехал мотоциклист и встретил автобус через 1 ч после выезда. С какой скоростью ехал автобус, если его скорость на 20 км/ч больше скорости мотоциклиста? Рабочий должен был обработать 80 деталей к определенному сроку. Он обрабатывал на 2 детали в час больше, чем планировал, и уже за 1 ч до срока обработал на 4 детали больше. Сколько деталей в час обрабатывал рабочий? За определенное время на автозаводе должны были собрать 160 автомобилей. Первые 2 ч выполнялась установленная почасовая норма, а затем стали собирать на 3 автомобиля в час больше. В результате за 1 ч до срока было собрано 155 автомобилей. Сколько автомобилей в час планировали собирать первоначально? |
| ВАРИАНТ 3 Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от пункта А. Найдите скорость каждого, если известно, что пешеход, вышедший из А, шел со скоростью, на 1 км/ч большей, чем другой пешеход, и сделал в пути 30-минутную остановку. Группа туристов отправляется на лодке от лагеря по течению реки с намерением вернуться обратно через 5 ч. Скорость течения реки 2 км/ч, собственная скорость лодки 8 км/ч. На какое наибольшее расстояние по реке они могут отплыть, если перед возвращением они планируют пробыть на берегу 3 ч? Два сотрудника типографии вместе набрали на компьютере 65 страниц, причем первый работал на 1 ч больше, чем второй. Однако второй набирает в час на 2 страницы больше, чем первый, и поэтому он набрал на 5 страниц больше. Сколько страниц в час набирает каждый сотрудник? На двух копировальных машинах, работающих одновременно, можно сделать копию пакета документов за 10 мин. За какое время можно выполнить эту работу на каждой машине в отдельности, если известно, что на первой машине ее можно сделать на 15 мин быстрее, чем на второй? | ВАРИАНТ 4 Из пунктов А и В, расстояние между которыми 34 км, выехали одновременно навстречу друг другу два мотоциклиста. Мотоциклист, выехавший из А, ехал со скоростью, на 8 км/ч большей скорости другого мотоциклиста, и сделал в пути получасовую остановку. Найдите скорость каждого, если известно, что они встретились в 10 км от пункта А Рыболов отправляется на лодке от пристани против течения реки с намерением вернуться назад через 5 ч. Перед возвращением он хочет побыть на берегу 2 ч. На какое наибольшее расстояние он может отплыть, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч? Кондитер и его ученик вместе изготовили 140 пирожных, причем кондитер работал на 1 ч меньше, чем ученик. Известно, что кондитер изготавливает в час на 6 пирожных больше, поэтому он изготовил на 20 пирожных больше, чем ученик. Сколько пирожных В час изготавливает кондитер и сколько ученик? На двух множительных аппаратах, работающих одновременно, можно сделать копию рукописи за 20 мин. За какое время можно выполнить эту работу на каждом аппарате в отдельности, если известно, что при работе на первом для этого потребуется на 30 мин меньше, чем при работе на втором? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 | 2 | 3 | 4 |
| Вариант 1 | 960 | 80 | 7 | 12 |
| Вариант 2 | 180 | 100 | 12 | 20 |
| Вариант 3 | 5 | 7,5 | 5 и 7 | 15 и 30 |
| Вариант 4 | 6 | 8 | 16 и 10 | 30 и 60 |
Правильные ответы:
План урока на тему «Решение задач с помощью уравнений»
(7 класс)
Цель урока: формирование умения использовать аппарат уравнений как средство для решения текстовых задач
План урока:
| № | Этап | Содержание | Время (мин) |
| 1 | Организационный момент | Нацелить учащихся на урок | 1 |
| 2 | Проверка домашнего задания | Коррекция ошибок | 5 |
| 3 | Актуализация опорных знаний | Устная работа | 3 |
| 4 | Математический диктант | Актуализация опорных знаний | 6 |
| 5 | Изложение нового материала | Показать учащимся возможность использования уравнений как средства для решения текстовых задач | 6 |
| 6 | Закрепление нового материала | Формировать умения ре6шать текстовые задачи с помощью уравнений | 10 |
| 7 | Решение задач с помощью таблиц или графов | Формировать умения ре6шать текстовые задачи с помощью уравнений | 6 |
| 8 | Тренировочные упражнения | Формировать умения ре6шать текстовые задачи с помощью уравнений | 5 |
| 9 | Подведение итогов урока | Обобщить теоретические сведения, полученные на уроке | 1 |
| 10 | Сообщение домашнего задания | Разъяснить содержание домашнего задания | 2 |
Организационный момент
Проверка домашнего задания (фронтально)
Опрос учащихся у доски №163(1), №164 (2)
Актуализация опорных знаний

Математический диктант (под копирку, с последующей проверкой)

Заслушать ответы учащихся, работавших у доски №163(1), №164 (2), проверить математический диктант
Изложение нового материала:
Решить задачу - значит найти неизвестное число, о котором говорится в ее условии. Этим числом могут быть: цена, числовые значения периметра, площади, скорости, длины пути и т.п.
Применение уравнений позволяет упростить решение многих задач
Решение задачи с помощью уравнения осуществляется отдельными шагами:
Неизвестное число обозначают буквой, например х (чаще всего это число, которое надо найти).
Устанавливают зависимость, которая существует между неизвестным числом, обозначенным буквой х, и другими числами, заданными в условии задачи.
Эта зависимость записывается уравнением.
Решают уравнение.
Отвечают на вопрос задачи.
Для примера можно рассмотреть решение задач:
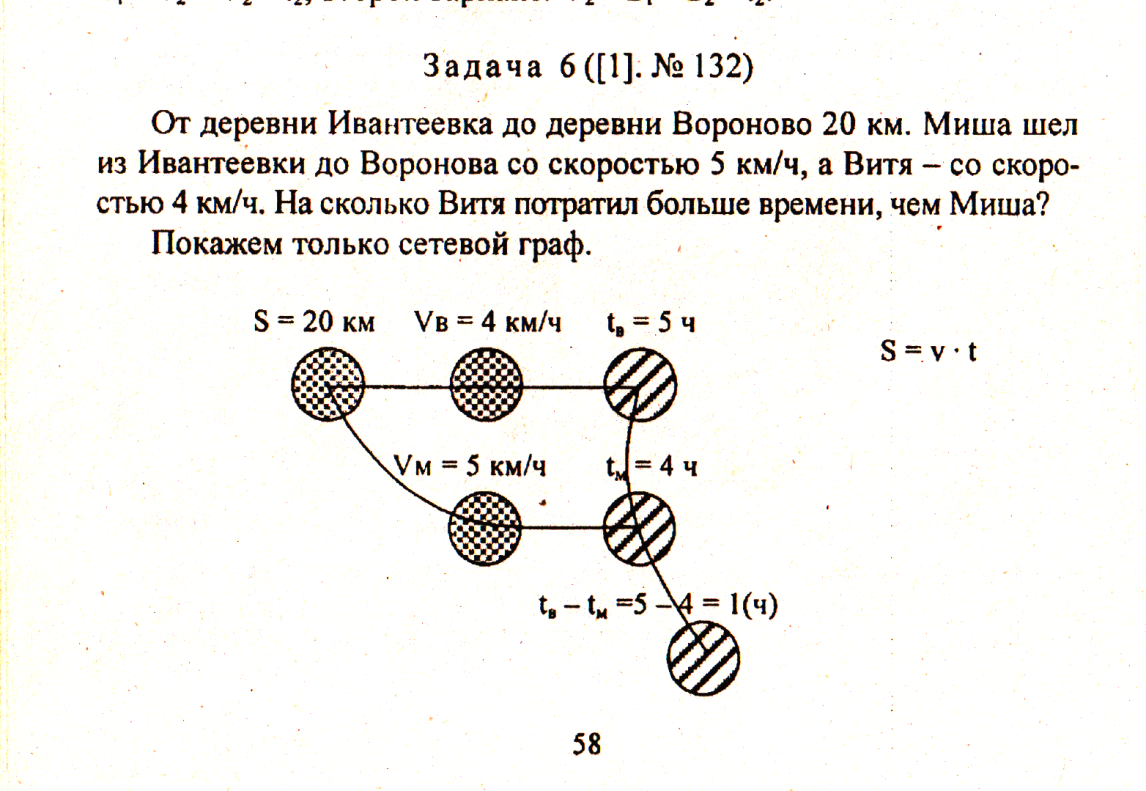
Закрепление нового материала
№№ 143, 145, 152 – с записью на доске и в тетрадях;
№ 144 – самостоятельно с последующей проверкой
Решение задач с помощью таблиц или графов
№№ 154, 155
Тренировочные упражнения
№№ 156, 157
Подведение итогов урока
Сообщение домашнего задания
П. 8 (контрольные вопросы), №№ 148, 151, 153, 165.
Заключение
Среднее (полное) общее образование - завершающая ступень общего образования, призванная обеспечить функциональную грамотность и социальную адаптацию обучающихся. Эти функции определяют направленность целей на формирование социально грамотной и социально мобильной личности, осознающей свои гражданские права и обязанности, ясно представляющих себе потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути. Эффективная реализация указанных целей возможна при введении профильного обучения, которое является «системой специализированной подготовки (профильного обучения) в старших классах общеобразовательных школ, ориентированной на индивидуализацию обучения и социализацию обучающихся, в том числе с учетом реальных потребностей рынка труда, отработки гибкой системы профилей и кооперации старшей ступени школы с учреждениями начального, среднего и высшего профессионального образования».
Переход к профильному обучению постепенный. Этому способствуют и элективные курсы - обязательные курсы по выбору учащихся из компонента общеобразовательного учреждения, входящие в состав профиля обучения.
Элективные курсы, как составная часть предпрофильной подготовки, выполняют несколько функций:
- надстройки профильного курса, когда такой дополненный профильный курс становится в полной мере углубленным;
- расширяют содержание одного из базисных курсов, изучение которого осуществляется на минимальном общеобразовательном уровне, что позволяет получить дополнительную подготовку для сдачи ЕГЭ по выбранному предмету, в данном случае, по математике;
- способствуют удовлетворению познавательных интересов в различных областях деятельности человека.
Профильное обучение в старших классах стало требованием времени, но переход к нему достаточно труден. Как учащимся и родителям выбрать нужный профиль? Что поможет сделать осознанный выбор профиля, соответствующего способностям и интересам?
Элективные курсы, проводимые в 8-9 классах, способствуют интенсификации образовательного процесса в целом и призваны помочь профессиональному ориентированию и самоопределению школьников.
Курс «Решение задач с помощью графов» содержит программу, тематическое планирование и рекомендации по проведению занятии. Курс «Решение задач с помощью графов» способствует углублению знаний о способах решения тестовых задач знакомит с эффективным способом решения - сетевым графом. К данному курсу подобраны задания для самостоятельной работы, задачи повышенной трудности с решениями, ответами и дополнительными указаниями.
Анализ подготовки выпускников
11-х классов в 2008-2009 уч.году Красновой О.Е.
Таблица
| ФИО педагога, предмет | Квалификация | Стаж | Классы | Кол. учащихся, сд. ЕГЭ | Проф-й или непроф. | Ср. балл по школе | Ср. балл у данного педагога | Ср. балл по городу среди лицеев |
| Краснова О.Е. | вторая | 14 | 11 а 11 ф | 16 21 | Непроф. Непроф. | 61,19 | 57,125 55,8 | 65 |
Диаграммы
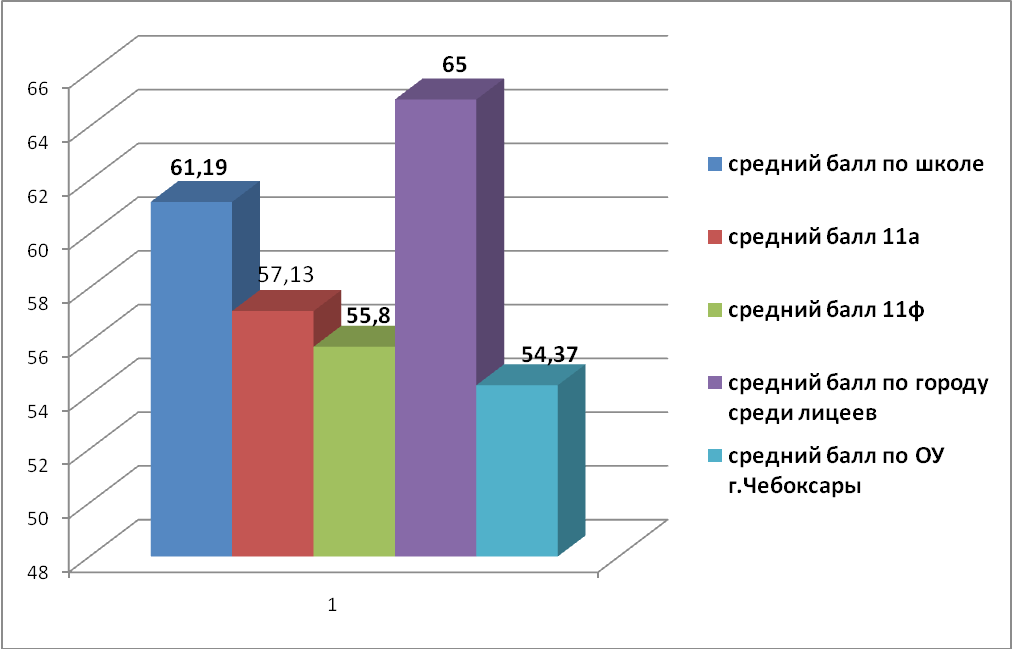
На диаграмме видно, что средний балл 11а класса и 11ф класса оказался ниже среднего балла по городу среди лицеев, это связано с тем, что профили этих классов гуманитарные и результаты ЕГЭ по математике для выпускников не являлись решающими для поступления в ВУЗы. Несмотря на это, результаты ЕГЭ по математике выше, чем средний балл по ОУ г. Чебоксары.
Литература
1. Математика: учебник для 5 кл. сред. шк. / Н. Я. Виленкин, В. И. Жохов и др. - М: Просвещение. 2008.
2. Алгебра: учеб. для 7, 8, 9 кл. общеобразовательных учреждений / Ю. Н. Макарычев и др.; под ред. С. А. Теляковского. - М.: Просвещевие,2009.
З. Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров и др. - М.: Просвещение, 2005
4. Ткачук, В. В. Математика - абитуриенту. – 15-е изд., исправленное и дополненное. М.: МЦНМО, 2008..
5. Сборник задач по математике для поступающих в вузы: учеб. пособие / под ред. М. И. Сканави. - М.: Столетие, 1997.
6. Кузнецова. Л. В. Алгебра: сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. - М.: Дрофа, 2002.
7. http://wiki.iteach.ru/index.php/Решение задач на работу с помощью сетевого графа


 Получите свидетельство
Получите свидетельство Вход
Вход


























 Методическая разработка по математике "Решение задач с помощью графов" (11.72 MB)
Методическая разработка по математике "Решение задач с помощью графов" (11.72 MB)
 0
0 2831
2831 135
135 Нравится
0
Нравится
0



