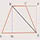
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
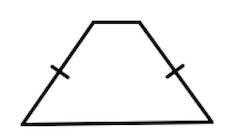
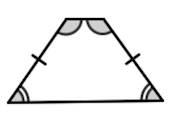
Если боковые стороны равны, трапеция называется равнобедренной.
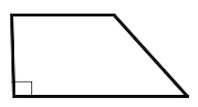
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
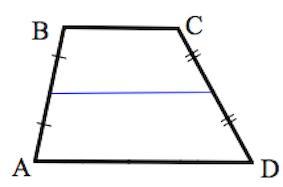
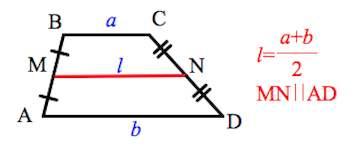
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции.
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

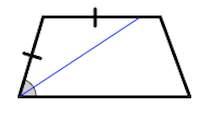
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
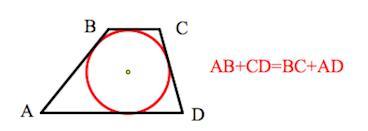
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
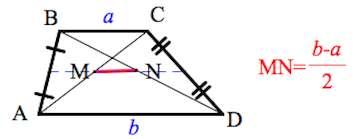
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
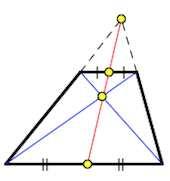
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
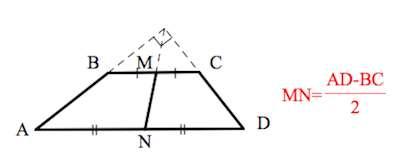
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции.
1. В равнобедренной трапеции углы при любом основании равны.
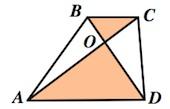
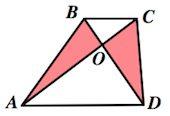
2. В равнобедренной трапеции длины диагоналей равны.
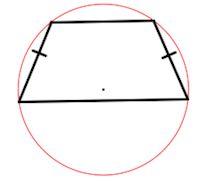
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
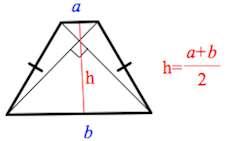
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Материал по математике на тему "Трапеция" (0.16 MB)
Материал по математике на тему "Трапеция" (0.16 MB)
 0
0 1593
1593 38
38 Нравится
0
Нравится
0