Предлагаемые задачи:

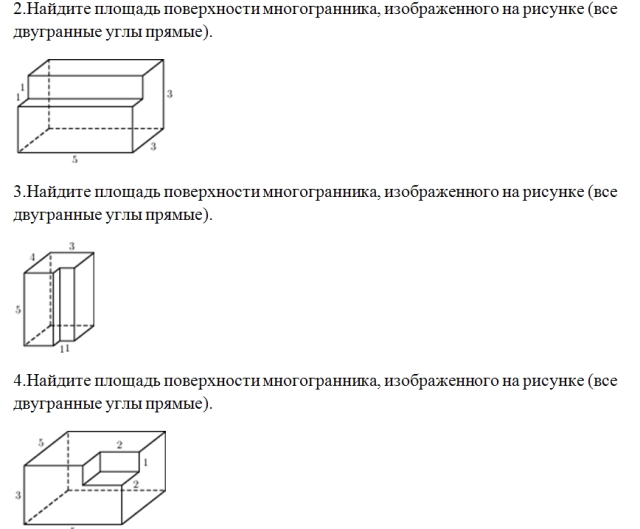
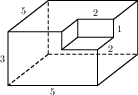
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
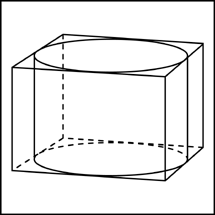
6. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Решение:
Высота цилиндра равна высоте параллелепипеда, а диаметр цилиндра равен стороне параллелепипеда. Зная формулу объема параллелепипеда V=a*b*c=S*h , можно вычислить объем. Получим a=d=2 V=2*2*1=4
Ответ: 4
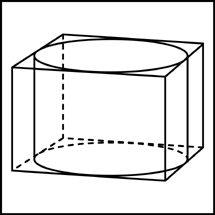
7. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
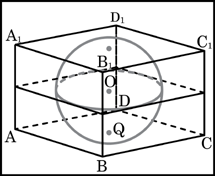
8. Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.
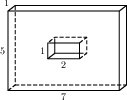
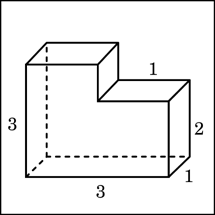
9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Решение:
Мысленно достроим многогранник до параллелепипеда и посчитаем объем получившегося параллелепипеда. V=3*3*1=9. Из получившегося объема вычислим объем параллелепипеда со сторонами 1,1,1. В результате объем равен 9-1=8.
Ответ: 8
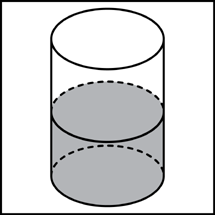
10 .В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в .
11. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в .
12. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Решение:
Первоначально высота жидкости была 16 см. При этом у неё был определённый радиус r и объем V=16πr². В новом сосуде изменился радиус и высота. Радиус можно узнать из условия, что диаметр нового сосуда в два раза больше первоначального. Значит, радиус нового сосуда равен двум радиусам первоначального, то есть 2r. Жидкость перелили в другой сосуд, значит, объем жидкости сохранился. Уравниваем объемы 16πr²=π(2r)²h=4πr²h
H=4см.
Ответ: 4 см.
13. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 25.
14. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
15. Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
16. Площадь поверхности куба равна 18. Найдите его диагональ.
17. Объем куба равен 8. Найдите площадь его поверхности.
18. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
19. Объем куба равен . Найдите его диагональ.
20. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
21. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра .
22. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
23. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
24. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
25. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
26. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
27. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
28. Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды .
29. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
30. Во сколько раз увеличится объем куба, если все его ребра увеличить в три раза?
31. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
32. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
33. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
34. Объем куба равен 66. Найти объем четырехугольной пирамиды, основанием которой является грань куба.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход


 Решение:
Решение:
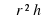
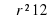 то ест
то ест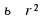 =
=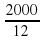
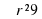 =
=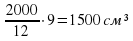
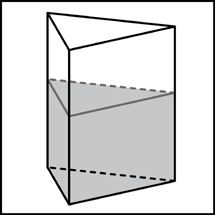
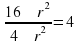 см.
см.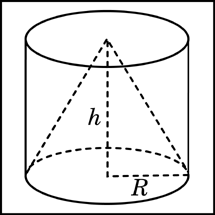
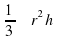 , а объем цилиндра по формуле
, а объем цилиндра по формуле








 Материал для подготовки к ЕГЭ 2014 по математике (0.22 MB)
Материал для подготовки к ЕГЭ 2014 по математике (0.22 MB)
 0
0 882
882 212
212 Нравится
0
Нравится
0


