Логика

Логика – наука о формах и способах мышления.

Логика – наука о формах и способах мышления.

• понятие,
• высказывание,
• умозаключение.

Понятие – форма мышления, фиксирующая основные, существенные признаки объекта.

Понятие имеет две стороны – содержание (совокупность существенных признаков объекта) и объем (совокупность предметов, на которую распространяется понятия).

Высказывание – форма мышления, в которой что – либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может либо истинно , либо ложно .

Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение)

Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний

В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения «истинно» и «ложно».

Истинно =1

Ложно=0

Таблица истинности

Для образования новых высказываний используются базовые логические операции:

инверсия

логическое отрицание

операция не

конъюнкция

дизъюнкция

логическое умножение

логическое сложение

операция и

операция или

Логическое отрицание -операция не - инверсия

А

А

НЕ

А(вход)

0

Ā (выход)

1

1

0

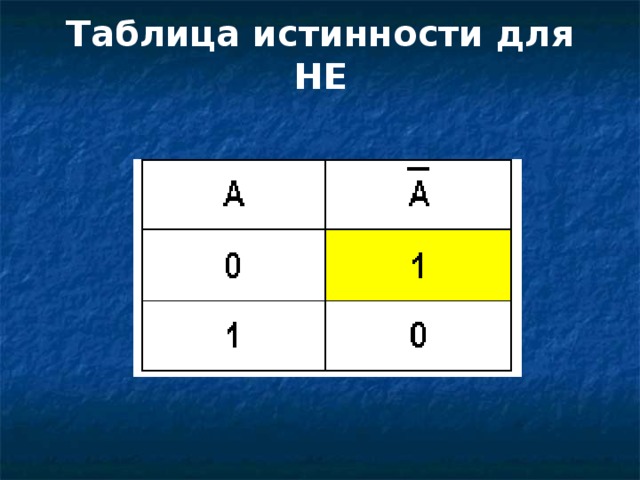
Таблица истинности для НЕ

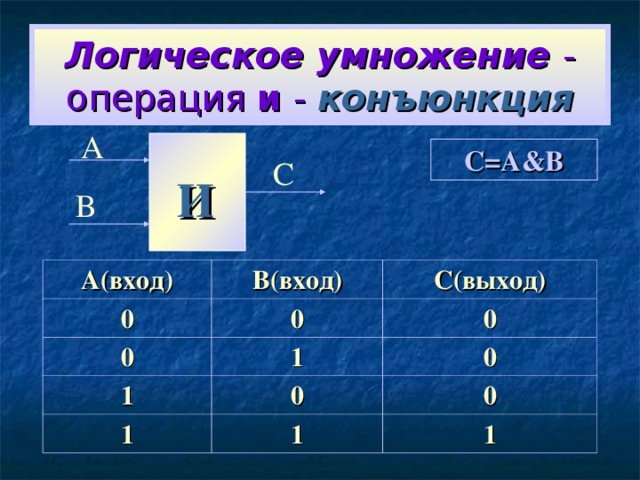
Логическое умножение - операция и - конъюнкция

А

C=A&B

С

И

В

А(вход)

0

В(вход)

0

С(выход)

0

0

1

1

1

0

0

0

1

1

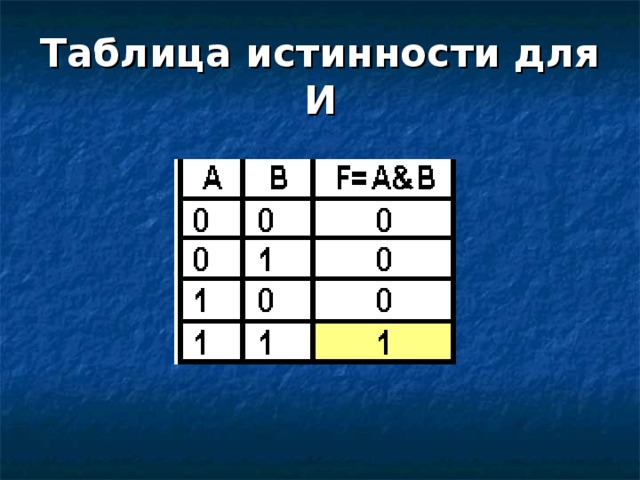
Таблица истинности для И

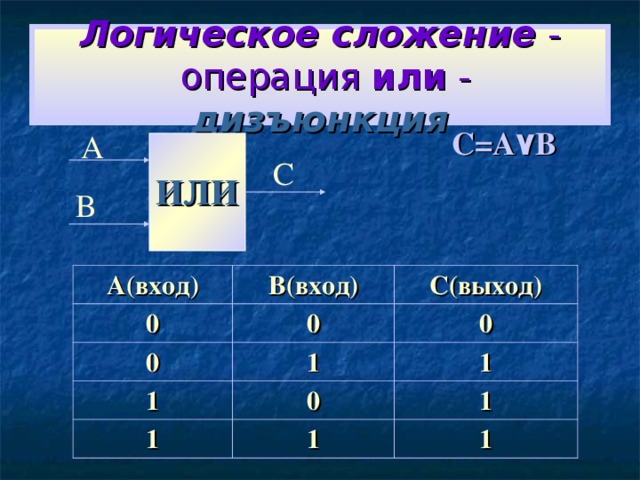
Логическое сложение - операция или - дизъюнкция

C=A ۷ B

А

С

ИЛИ

В

А(вход)

0

В(вход)

0

С(выход)

0

0

1

1

1

1

0

1

1

1

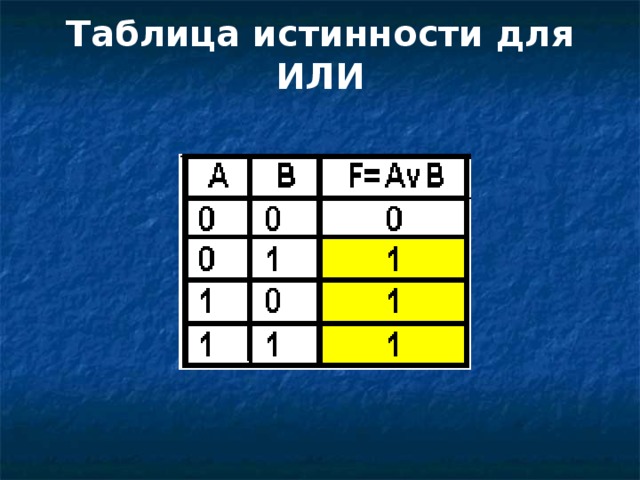
Таблица истинности для ИЛИ

Эквиваленция

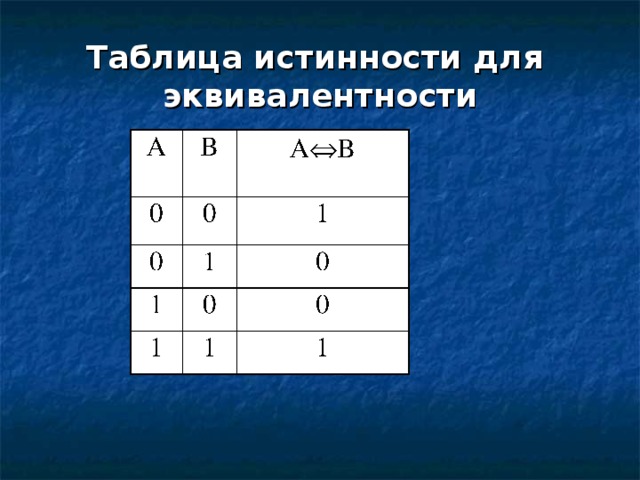
Таблица истинности для эквивалентности

А  В

В " width="640"

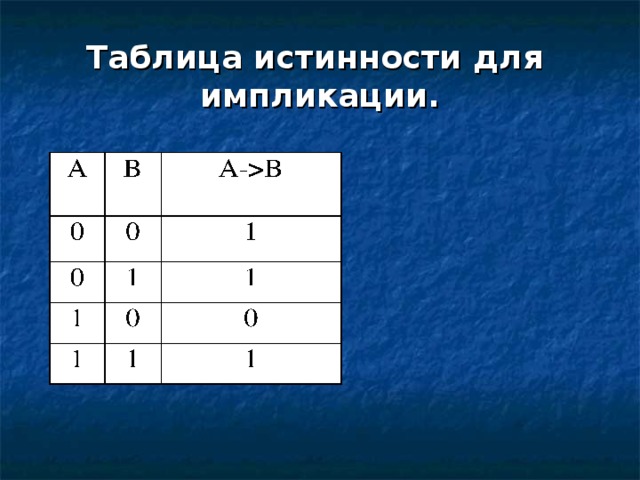
Таблица истинности для импликации.

А - В

Порядок выполнения логических операций



Логические законы и правила преобразования логических выражений

• Закон тождества : всякое высказывание тождественно самому себе.

А=А

• Закон непротиворечия: высказывание не может быть одновременно истинным и ложным.

А & А=1

• Закон исключенного третьего. Высказывание может быть истинным, либо ложным, третьего не дано.

А ۷ А=1

• Закон двойного отрицания: если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание.

А=А

Законы Моргана:

А ۷ В=А & В

А & В=А ۷ В