Презентация в себе содержит под темы:
1) Основные понятия;
2) История возникновения математической логики;
3) Формы мышления в логике;
4) Алгебра логики;
5) Логические операции (примеры).

1) Основные понятия.
Логика — наука о законах и правилах мышления.
Формальная логика — наука о законах и формах мышления.
Математическая логика - область знания в которой формальная логика изучается математическими методами.
2) История возникновения математической логики.
- 4 в. до н. э. древнегреческий ученый Аристотель заложил основы формальной логики;
- 17 в. немецкий математик Лейбниц – заложил
основы математической логики;
- 18 в. английский математик и логик Джордж Буль развил и сформулировал логические исчисления (поэтому иногда математическую логику называют Булевой алгеброй);
- 19 в. Готлоб Фреге, Чарльз Пирс, Бертран Рассел и др.
- В ПЕРВОЙ ПОЛОВИНЕ 20 в. МАТЕМАТИЧЕСКАЯ ЛОГИКА ПЕРЕШЛА В САМОСТОЯТЕЛЬНУЮ ДИСЦИПЛИНУ
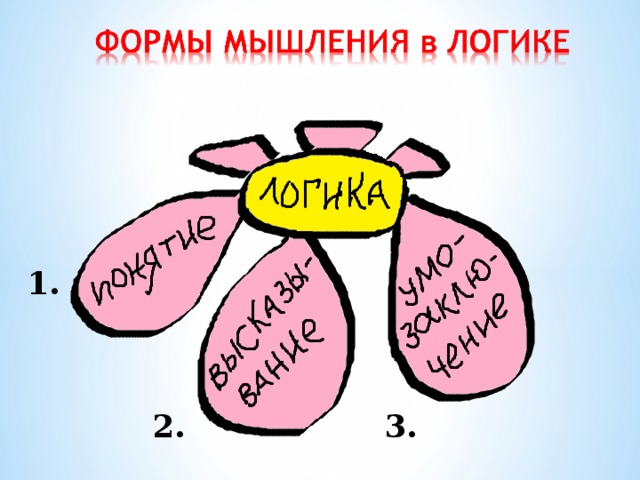
3) Формы мышления в логике.
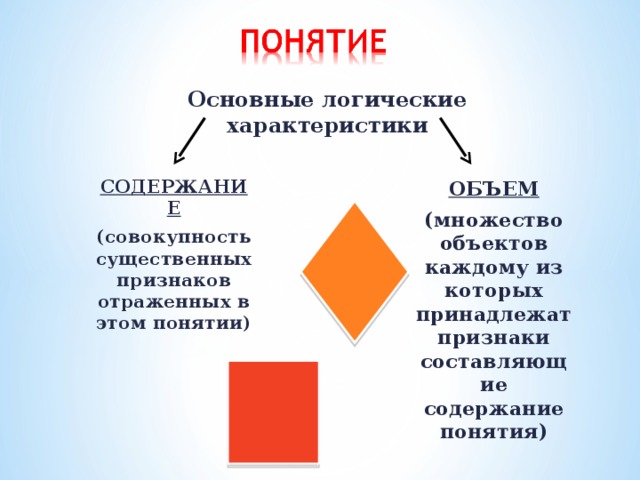
Понятие - это форма мышления, которая выделяет существенные признаки предмета или класса предметов, отличающие его от других.
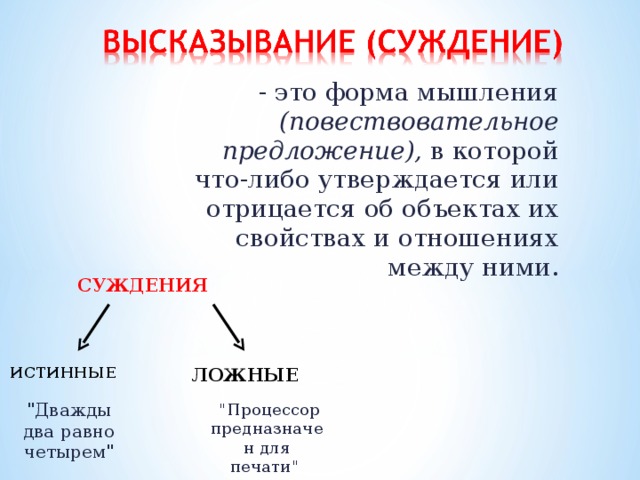
Суждение - это форма мышления (повествовательное предложение), в которой что - либо утверждается или отрицается об объектах их свойствах и отношениях между ними.
Умозаключение - это прием мышления, позволяющий на основе одного или нескольких суждений - посылок получить новое суждение (знание или вывод).
4) Алгебра логики.
Алгебра логики — это математический аппарат, с помощью которого записывается, вычисляется, упрощается и преобразуется логическое высказывание.
Основным понятием математической логики является высказывание.
Высказывание — это повествовательное предложение, про которое всегда можно сказать истинное оно или ложное.
Истинна — 1
Ложь — 0
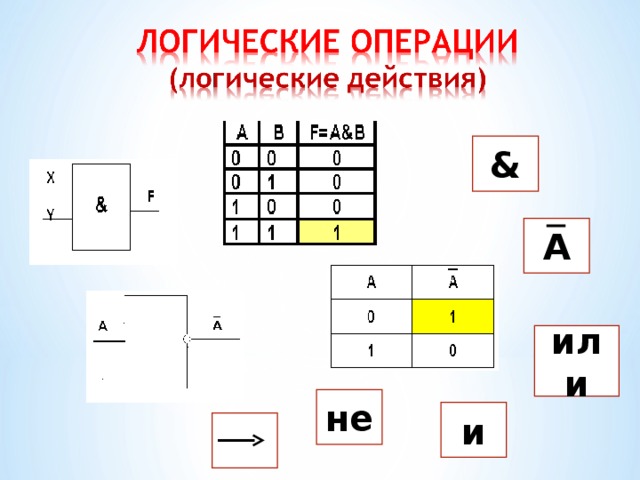
5) Логические операции.
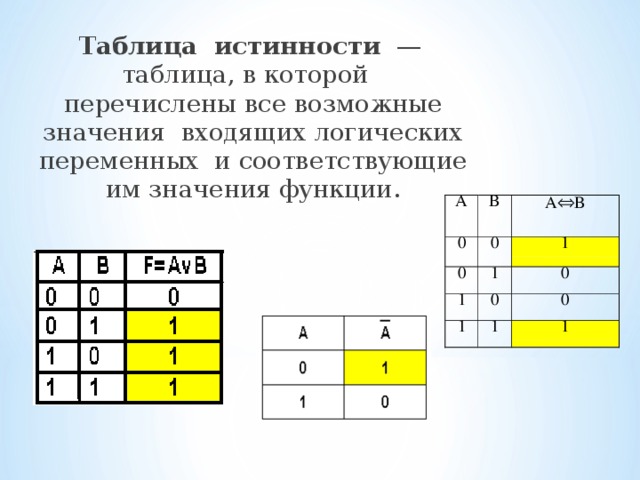
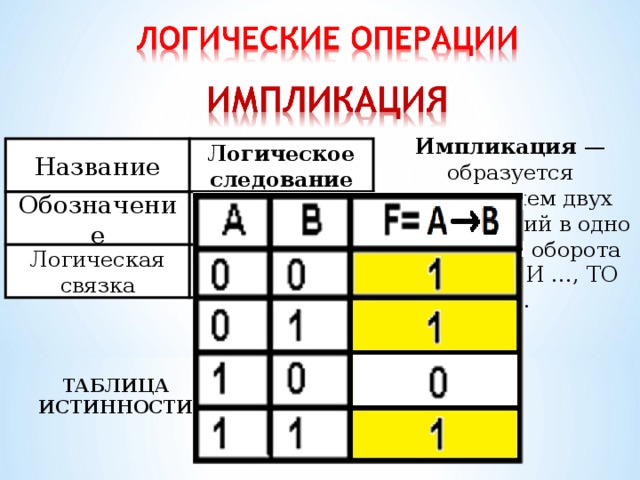
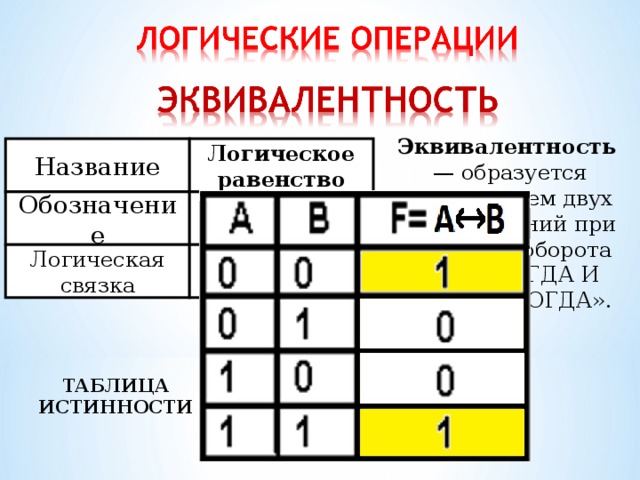
Таблица истинности — таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
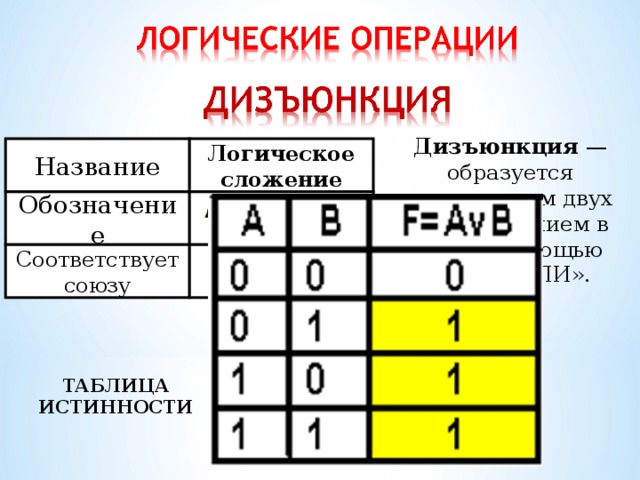
Дизъюнкция — образуется соединением двух высказыванием в одно с помощью союза «ИЛИ».
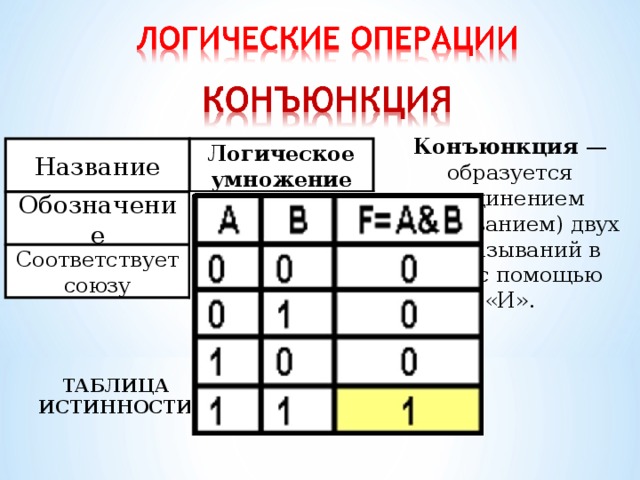
Конъюнкция — образуется соединением (связыванием) двух высказываний в одно с помощью «И».
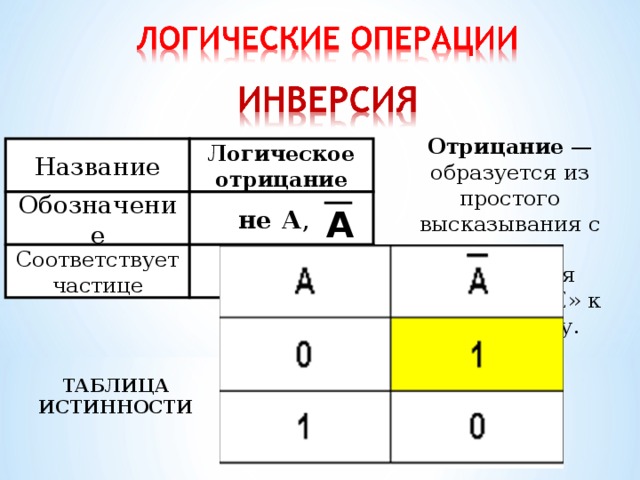
Отрицание — образуется из простого высказывания с помощью добавления частицы «НЕ» к сказуемому.
Импликация — образуется соединением двух высказываний в одно с помощью оборота речи «ЕСЛИ …, ТО …».
Эквивалентность — образуется соединением двух высказываний при помощью оборота речи «ТОГДА И ТОЛЬКО ТОГДА».
Задание для самостоятельного решения.
Составьте и запишите по 2 - 3 примера на каждую логическую операцию, а так же не забудьте представить свои высказывания на языке алгебры логики.

 Получите свидетельство
Получите свидетельство Вход
Вход

























 Презентация по информатике "Математическая логика. Основные понятия" (4.75 MB)
Презентация по информатике "Математическая логика. Основные понятия" (4.75 MB)
 0
0 2129
2129 429
429 Нравится
1
Нравится
1


