Линейные уравнения с параметрами

Методическая разработка занятия элективного курса

Системы линейных уравнений, содержащие параметр.

автор

Никитина Марина Геннадьевна

Кандидат педагогических наук, доцент

Санкт-Петербург

2017 г.

Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами наиболее трудной и важной частью решения таких задач является исследование процесса в зависимости от параметров. Решение таких задач требует не только знаний свойств функций и уравнений, умения выполнять алгебраические преобразования, но и высокой логической культуры и хорошей техники исследования.
В учебниках математики, по которым учатся наши дети, нет теоретических сведений и систематизированного набора заданий с параметрами, а вот в контрольно-измерительных материалах для сдачи ЕГЭ, такие задания имеются. Поэтому для хорошей подготовки и успешной сдачи экзамена данная разработка необходима.
Кроме того, эта разработка поможет довести решение простейших уравнений до автоматизма, а умение решать уравнения играет в математике огромную роль т. к. они являются неотъемлемой частью многих задач, систем, применяются при это поможет сэкономить время на экзамене, для более сложных заданий. 
Цель методической разработки:
Доведение до автоматизма применение алгоритмов решения систем линейных уравнений, изучаемых в основной школе.
Расширение спектра решаемых уравнений, посильных для обучающихся.
Задачи:
Обобщение, систематизация и углубление знаний по теме «Системы линейных уравнений, содержащие параметр.

Развитие познавательных интересов и творческих способностей обучающихся.
Предоставление обучающимся возможности проанализировать и оценить свои способности к математической деятельности.
Облегчение выбора профиля в средней школе.
Формы и методы работы.

Формы работы необходимые для успешной работы как общеклассные (при повторении необходимого теоретического материала или при систематизации тех или иных знаний), так и индивидуальные (при выполнении упражнений, сдаче зачёта), кроме того, можно использовать и групповые формы работы (при отыскании решения нестандартных, трудных систем уравнений).
Методы работы могут быть также разнообразными. От фронтального опроса (при повторении), до эвристической беседы (при объяснении необходимых новых теоретических сведений), а также создания ситуации успеха при выполнении самостоятельных работ.
Главное, чтобы формы и методы работы располагали к самостоятельному поиску решений, повышать интерес к изучению предмета, развивать интуицию и скорость мышления.

Планируемые результаты.

Произойдёт расширение знаний, облегчение решения некоторых задач, требующих создания и исследования математической модели.
Данная математическая разработка даст учителю возможность поможет учителю ,который применяет на своих уроках что-то подчеркнуть ему еще неизвестное или сэкономить время при подготовке к элективному занятию.

.

Системы линейных уравнений, содержащие параметр.

Цель: обобщить знания учащихся по теме линейные уравнения, системы линейных уравнений, графики линейной функции, корни системы линейных уравнений, определяемые по графикам. Применить эти знания на более высоком уровне понимания в системах, содержащих параметр.

Ход занятия:

1.Повторить уравнение прямой, записанное с угловым коэффициентом.

y=kx+b y=5x+3 y=6x+7

2.Записать уравнение в общем виде.

ax + by + c=0 5x-y-3=0 6x-y+7=0

3.Уравнение прямой на плоскости записывается в виде: .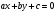

Две прямые и совпадают, если ,

параллельны, если ,

пересекаются, если .

Если рассматривать систему из двух линейных уравнений:,

то по аналогии с вышесказанным: система имеет одно решение при ;

ни одного решения при ;

множество решений при .

4. Как это реализуется на практике.

Пример 1. При каких значениях параметра система 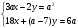не имеет решений, имеет множество решений, имеет одно решение?

Решение. Для того, чтобы данная система не имела решений, необходимо выполнение условия: .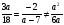

Решая уравнение 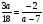или 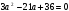, находим . Подстановкой убеждаемся, что при 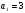не выполнено неравенство 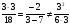, а при неравенство 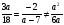выполнено, т.е. при 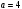система не имеет решений, при система имеет множество решений и при и при 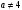система имеет единственное решение.

5. Задачи для самостоятельного решения.

Проверить на доске. Вызвать двух учеников.

1. При каких значениях параметра система не имеет решений.

2. Найти все значения параметра , при которых система не имеет решений.

3. При каких значениях параметра система имеет единственное решение.

4. При каких значениях для любого существует хотя бы одно такое, что система имеет решение.

5. Задания на карточках для выполнения во время самоподготовки.

1. Исследовать систему уравнений:

.

2. Исследовать систему уравнений:

.

3. Исследовать систему уравнений:

.

4. Исследовать систему уравнений:

.

7. Итог занятия.

Сегодня мы занимались математическим моделированием. Мы моделировали математические ситуации, связанные с расположением прямых на плоскости. Не решая уравнения, а анализируя коэффициенты, мы подбирали различные значения параметров. Этот метод предполагает понимания Вами особенности данной системы. В задаче №18 на ЕГЭ возможна такая задача, содержащая систему линейных уравнений и параметр, но наверняка она будет обременена дополнительными сложностями. Ваша задача увидеть систему линейных уравнений, вспомнить условия при которых система имеет одно решение, бесконечно много решений или не имеет решений. А дальше уже поймете что делать. Не бойтесь, моделируйте, анализируйте. Задачи с параметром это новый уровень осознания Вами математики.

8. Рефлексия. Ребята. Достаточно ли я доходчиво объяснила тему «Системы линейных уравнений, содержащие параметр»?