Уравнение (неравенство) с параметрами — математическое уравнение (неравенство), внешний вид и решение которого зависит от значений одного или нескольких параметров.
Решить уравнение с параметром означает:
Найти все системы значений параметров, при которых данное уравнение имеет решение.
Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.
Уравнения с параметром могут быть как линейными, так и нелинейными.
Пример линейного уравнения с параметром:
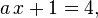
Пример нелинейного уравнения с параметром:
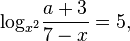
где 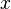 — независимая переменная
— независимая переменная 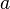 — параметр.
— параметр.
Аналогично подразделяются и неравенства. Ниже будут представлены примеры решений уравнений и неравенств с параметрами.
Примеры
Пример 1.При каком 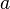 квадратное уравнение
квадратное уравнение 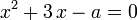 имеет ровно один корень?
имеет ровно один корень?
Решение. Любое квадратное уравнение имеет одно решение, когда его дискриминант равен нулю. Итак, дискриминант нашего уравнения: 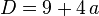 . Далее имеем:
. Далее имеем: 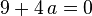 , откуда
, откуда 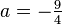 .
.
Ответ: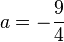 .
.
Пример 2. При каком 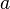 система уравнений :
система уравнений :
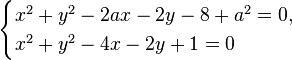 .
.
имеет ровно два решения?
Решение. Сначала надо преобразовать два уравнения системы, выделив в них полные квадраты: 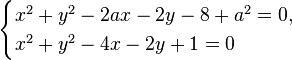

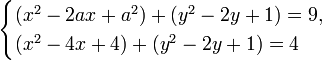

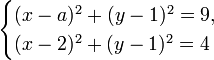
Нетрудно догадаться, что эти два равенства системы есть ни что иное, как уравнения окружностей. Первая окружность имеет центр в точке 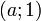 , радиус
, радиус 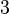 , а вторая центр в точке
, а вторая центр в точке 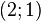 и радиус
и радиус 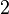 . Если построить схематично эти окружности в одной системе координат, то можно заметить, что их общих точек пересечения будет две в том случае, если
. Если построить схематично эти окружности в одной системе координат, то можно заметить, что их общих точек пересечения будет две в том случае, если 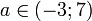 . И задачу можно считать решённой.
. И задачу можно считать решённой.
Ответ: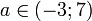 .
.
Пример 3. При всех 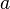 решить неравенство
решить неравенство 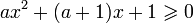 .
.
Решение. Рассмотрим три случая:
Если  , то неравенство приобретает вид ;
, то неравенство приобретает вид ;
Если  , то все коэффициенты квадратного трехчлена будут положительны, значит, решение неравенства можно представить в виде , где
, то все коэффициенты квадратного трехчлена будут положительны, значит, решение неравенства можно представить в виде , где  ,
, - корни многочлена и
- корни многочлена и  . Далее находим:
. Далее находим:
Следовательно, , если  и , если
и , если  .
.
3. Если  , то ветви параболы направлены вниз, естественно решение в общем виде будет выглядеть вот так: .
, то ветви параболы направлены вниз, естественно решение в общем виде будет выглядеть вот так: .
Нам остается лишь записать ответ.
Ответ: если  , то ; если
, то ; если  , то ; если
, то ; если  , то ; если
, то ; если  , то
, то  .
.


 Получите свидетельство
Получите свидетельство Вход
Вход


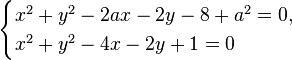 .
.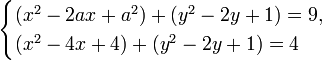
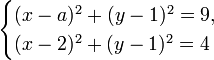









 Уравнение (неравенство) с параметрами (методический материал) (46.46 КB)
Уравнение (неравенство) с параметрами (методический материал) (46.46 КB)
 0
0 901
901 73
73 Нравится
0
Нравится
0





