Программа элективного курса "Алгебра"
11 класс
Пояснительная записка.
Программа составлена на основе программы элективного курса « Алгебра +: рациональные и иррациональные алгебраические задачи». Автор Земляков А.Н., Москва, Бином, Лаборатория знаний, 2007 год.
Программа курса предназначена для углубления знаний по математике, для поддержки основного базового курса, а так же для подготовки учащихся к экзаменам.
Рабочая программа рассчитана на 68 часов. Программа автора Землякова А.Н. рассчитана на 48 часов. Поэтому в программу добавлены 20 часов, это позволяет сделать разработанный автором курс, за счет рассмотрения на занятиях тех тем, которые автор предлагает для самостоятельного обучения. Программа курса предполагает развитие у школьников навыков организации умственного труда и самообразования, распознание и раскрытие их способностей.
Цели элективного курса:
повысить математическую культуру учащихся при решении задач повышенного уровня в рамках школьного курса математики;
дать учащимся, проявляющим повышенный интерес к математике, возможность углубленного изучения основного курса путем рассмотрения задач, требуемых нестандартного подхода при своем решении.
сформировать и отработать навыки исследовательской деятельности учащихся на содержательном теоретическом материале и специально подобранных практических упражнениях, развить интерес и склонности учащихся к математике и потенциальные творческие способности учащихся, не ограничивая заранее сверху уровень сложности используемого задачного материала;
создать общее представление об элементарной алгебре и применяемых в ней методах как о составляющей всей математики как науки.
Задачи:
получение знаний об основных логических и содержательных типах алгебраических задач: уравнений, неравенств, систем, совокупностей с рациональными, иррациональными функциями/ выражениями; овладение навыками соответствующих алгебраических преобразований выражений и логических преобразований алгебраических задач;
овладение логическими, аналитическими, графическими методами решения алгебраических задач с изучаемыми классами функций и выражений;
освоение методов решения и исследования вычислительных и логических задач с параметрами;
получение конкретного представления о взаимосвязях высшей математики с элементарной алгеброй.
Ожидаемый результат:
Методическое обеспечение
1. Земляков А.Н., Элективный курс « Алгебра +: рациональные и иррациональные алгебраические задачи». Учебное пособие.Москва, Бином, Лаборатория знаний, 2006 год
2. Земляков А.Н., Элективный курс « Алгебра +: рациональные и иррациональные алгебраические задачи». Методическое пособие. Москва, Бином, Лаборатория знаний, 2007 год
Структура курса
Логика алгебраических задач – 8 ч
Многочлены и полиноминальные алгебраические уравнения – 15 ч
Рациональные алгебраические уравнения и неравенства – 10 ч
Рациональные алгебраические системы – 19 ч
Иррациональные алгебраические задачи – 16 ч
Тематическое планирование
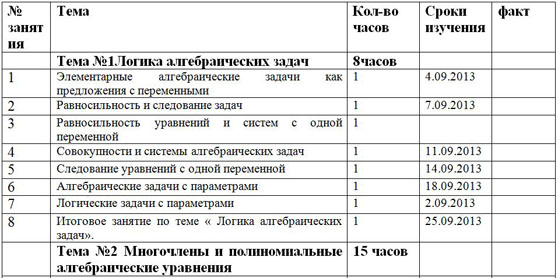
| № занятия | Тема | Кол-во часов | Сроки изучения | факт |
|
| Тема №1Логика алгебраических задач | 8часов |
|
|
| 1 | Элементарные алгебраические задачи как предложения с переменными | 1 | 4.09.2013 |
|
| 2 | Равносильность и следование задач | 1 | 7.09.2013 |
|
| 3 | Равносильность уравнений и систем с одной переменной | 1 |
|
|
| 4 | Совокупности и системы алгебраических задач | 1 | 11.09.2013 |
|
| 5 | Следование уравнений с одной переменной | 1 | 14.09.2013 |
|
| 6 | Алгебраические задачи с параметрами | 1 | 18.09.2013 |
|
| 7 | Логические задачи с параметрами | 1 | 2.09.2013 |
|
| 8 | Итоговое занятие по теме « Логика алгебраических задач». | 1 | 25.09.2013 |
|
|
| Тема №2 Многочлены и полиномиальные алгебраические уравнения | 15 часов |
|
|
| 9 | Многочлены. Степень многочлена. Кольца многочленов. | 1 | 28.09.2013 |
|
| 10 | Делимость и деление многочленов | 1 | 2.10.2013 |
|
| 11 | Теорема Безу. Корни многочленов. | 1 | 5.10.2013 |
|
| 12 | Делимость многочленов на двучлен | 1 | 9.10.2013 |
|
| 13 | Полностью разложимые многочлены. Теоремы Виета | 1 | 12.10.2013 |
|
| 14 | Формула Ньютона. Треугольник Паскаля | 1 | 16.10.2013 |
|
| 15 | Квадратный трехчлен: линейная замена, график, корни, разложение, теорема Виета. | 1 | 19.10.2013 |
|
| 16 | Квадратичные неравенства, метод интервалов. | 1 | 23.10.2013 |
|
| 17 | Кубические многочлены. Решение кубических уравнений. | 1 | 26.10.2013 |
|
| 18 | Уравнения 4 степени: схема Феррари | 1 | 30.10.2013 |
|
| 19 | Простейшие полиномиальные уравнения | 1 |
|
|
| 20 | Линейные замены, основанные на симметрии | 1 | 13.11.2013 |
|
| 21 | Метод разложения. Поиск рациональных корней | 1 | 16.11.2013 |
|
| 22 | Разложение методом неопределенных коэффициентов | 1 | 20.11.2013 |
|
| 23 | Итоговое занятие по теме « Многочлены» | 1 | 23.11.2013 |
|
|
| Тема №3 Рациональные алгебраические уравнения и неравенства | 10 часов |
|
|
| 24 | Рациональные алгебраические выражения и задачи | 1 | 27.11.2013 |
|
| 25 | Метод замены | 1 | 30.11.2013 |
|
| 26 | Симметричные уравнения. | 1 | 4.12.2013 |
|
| 27 | Кососимметричные уравнения. | 1 | 7.12.2013 |
|
| 28 | Простейшие рациональные неравенства. | 1 | 11.12.2013 |
|
| 29 | Методы решения рациональных алгебраических неравенств. | 1 | 14.12.2013 |
|
| 30 | Сведение к системам неравенств | 1 | 18.12.2013 |
|
| 31 | Метод интервалов | 1 | 21.12.2013 |
|
| 32 | Метод замены | 1 | 25.12.2013 |
|
| 33 | Неравенства с двумя переменными | 1 | 28.12.2013 |
|
|
| Тема 4 Рациональные алгебраические системы | 19 |
|
|
| 34 | Решение уравнений с двумя переменными | 1 | 15.01.2014 |
|
| 35 | Однородные уравнения с двумя переменными | 1 | 18.01.2014 |
|
| 36 | Решение систем. Метод подстановки. | 1 | 22.01.2014 |
|
| 37 | Однородные системы | 1 | 25.01.2014 |
|
| 38 | Метод замены | 1 | 29.01.2014 |
|
| 39 | Симметричные системы | 1 | 01.02.2014 |
|
| 40 | Системы Виета | 1 | 5.02.2014 |
|
| 41 | Решение систем методом разложения | 1 | 8.02.2014 |
|
| 42 | Метод оценок | 1 | 12.02.2014 |
|
| 43 | Метод итераций | 1 | 15.02.2014 |
|
| 44 | Сведение уравнений к системам | 1 | 19.02.2014 |
|
| 45 | Оценка значений переменных | 1 | 22.02.2014 |
|
| 46 | Системы с тремя переменными. Метод подстановки. | 1 | 26.02.2014 |
|
| 47 | Метод замены | 1 | 1.03.2014 |
|
| 48 | Использование однородности | 1 | 5.03.2014 |
|
| 49 | Система Виета с тремя переменными | 1 | 12.03.2014
|
|
| 50 | Симметричные системы | 1 | 15.03.2014
|
|
| 51-52 | Метод разложения | 2 | 19.03.2014 22.03.2014 |
|
|
| Тема 5 Иррациональные алгебраические задачи | 16 часов |
|
|
| 53- 54 | Иррациональные алгебраические выражения. Уравнения с квадратными радикалами. Замена переменной | 2 | 2.04.2014 5.04.2014 |
|
| 55 | Неэквивалентные преобразования с проверкой | 1 | 9.04.2014 |
|
| 56 | Метод эквивалентных преобразований | 1 | 12.04.2014 |
|
| 57 | Сведение уравнений к системам | 1 | 16.04.2014 |
|
| 58 | Освобождение от кубических радикалов | 1 | 19.04.2014 |
|
| 59 | Использование монотонности. Использование однородности. | 1 | 23.04.2014 |
|
| 60 | Неравенства с радикалами. Почему неравенства с радикалами сложнее уравнений | 1 | 26.04.2014 |
|
| 61 | Метод интервалов при решении иррациональных неравенств | 1 | 30.04.2014 |
|
| 62 | Использование монотонности при решении неравенств | 1 | 03.05.2014 |
|
| 63-64 | Уравнения с модулями | 2 | 07.05.2014 10.05.2014 |
|
| 65-66 | Неравенства с модулями | 2 | 14.05.2014 17.05.2014 |
|
| 67-68 | Комбинированные задачи с модулями | 2 | 21.05.2014 24.05.2014 |
|
|
| Итого часов | 68 |
|
|
Предметные умения, которыми должны овладеть учащиеся по изучении данного курса:
- умение проводить логически грамотные преобразования выражений и эквивалентные преобразования алгебраических задач (уравнений, неравенств, систем, совокупностей);
- умение использовать основные методы при решении алгебраических задач с различными классами функций (рациональными и иррациональными алгебраическими), в том числе: методы замены, разложения, подстановки, эквивалентных преобразований, использования симметрии, однородности, оценок, монотонности;
- умение принимать и правильно интерпретировать задачи с параметрами, логические и кванторные задачи; умение применять изученные методы исследования и решения задач с параметрами: аналитический и координатный.
Общеинтеллектуальные умения:
- умение анализировать различные задачи и ситуации, выделять главное, достоверное в той или иной информации;
- владение логическим, доказательным стилем мышления, умение логически обосновывать свои суждения;
- умение конструктивно подходить к предлагаемым задачам;
- умение планировать и проектировать свою деятельность, проверять и оценивать её результаты.
Общекультурные компетенции:
- понимание элементарной математики как неотъемлемой части математики, методы которой базируются на многих разделах математики высшей;
- понимание роли элементарной математики в развитии математики, роли математиков в развитии современной элементарной математики;
- восприятие математики как развивающейся фундаментальной науки, являющейся неотъемлемой составляющей науки, цивилизации, общечеловеческой культуры во взаимосвязи и взаимодействии с другими областями мировой культуры.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Программа элективного курса "Алгебра+" (11 класс) (0.11 MB)
Программа элективного курса "Алгебра+" (11 класс) (0.11 MB)
 0
0 1595
1595 183
183 Нравится
0
Нравится
0



