Муниципальное казенное общеобразовательное учреждение Тагарская СОШ Кежемского района Красноярского края
|
РАССМОТРЕНО На заседании МО учителей математики Протокол № ____________ от «___» __________2013 г. Руководитель МО
|
СОГЛАСОВАНО Заместитель директора МКОУ Тагарской СОШ О.И.Безруких
___________________
«___» _________2013 г. |
УТВЕРЖДЕНО Директор МКОУ Тагарской СОШ А.А. Рукосуев
____________________ Приказ № ___________ «___» _______ 2013 г. |
РАБОЧАЯ ПРОГРАММА
элективного учебного курса
по математике
«Алгебра плюс: элементарная алгебра
с точки зрения высшей математики»
для 10-11 класса
на 2013 – 2014 учебный год
ступень обучения: общее образование
уровень: базовый
Составитель:
Титов Антон Олегович
учитель математики
д. Тагара, 2013-2014 учебный год
Пояснительная записка
Рабочая программа элективного учебного предмета «Алгебра плюс: Элементарная алгебра с точки зрения высшей математики» для учащихся 10 – 11 класса составлена на основе авторской программы А.Н. Землякова, кандидата пед. наук, ведущего научного сотрудника лаборатории дифференциации образования ЦЭПД РАО, г.Черниголовка, Московская обл. Из этой программы взяты модули «Рациональные алгебраические уравнения и неравенства», «Рациональные алгебраические системы», «Иррациональные алгебраические задачи». Из этих модулей исключены несколько тем, не нарушающих их логику. Программа рассчитана на 69 часов (10 – 11 класс), исходя из расчёта 1 час в неделю.
Данная программа элективного курса по математике даёт широкие возможности повторения и обобщения курса алгебры и основ анализа. В курсе разбирается большое количество сложных задач, которые понадобятся учащимся как при учёбе в высшей школе, так и при подготовке к ЕГЭ. Темы, предложенные этой программой, значительно расширяют и углубляют уровень знаний, предусмотренных базовым уровнем общеобразовательной программы по алгебре и началам анализа в 10 – 11 классе.
Цель курса:
повторение и обобщение курса алгебры и основ анализа, знакомство учащихся с материалом, не предусмотренным государственной программой, но который необходимо знать абитуриенту, желающему поступить в ВУЗ. В курсе предусмотрено решение большого числа сложных задач, многие из которых понадобятся как при учебе в высших учебных заведениях, так и при подготовке к Единому государственному экзамену.
Задачи курса:
знакомство учащихся с разнообразными методами решения задач как соответствующих программному материалу, так и более сложных задач, выходящих за рамки программного материала, в частности рассматриваются методы решения уравнений высших степеней, решение неравенств и уравнений, содержащих модули, решения задач с параметрами.
Календарное поурочно-тематическое планирование элективного учебного предмета для учащихся 10 класса «Алгебра плюс: элементарная алгебра с точки зрения высшей математики».
1 час в неделю, всего 35 часов
| № урока | Содержание программного материала | Кол-во часов | Сроки | Примечание |
|
| Рациональные алгебраические уравнения
| 25 |
|
|
| 1. | Представление о рациональных алгебраических выражениях. | 1 |
|
|
| 2-3 | Симметрические и возвратные многочлены и уравнения. | 2 |
|
|
| 4-5 | Дробно – рациональные алгебраические уравнения. Общая схема решения. | 2 |
|
|
| 6-8 | Методы замены при решении дробно – рациональных уравнений. | 3 |
|
|
| 9-10 | Дробно – рациональные алгебраические неравенства. Общая схема решения методом сведения к совокупностям системы. | 2 |
|
|
| 11-13 | Метод интервалов решения дробно – рациональных алгебраических неравенств. | 3 |
|
|
| 14-15 | Метод оценки. Использование монотонности. Метод замены при при решении уравнений. | 2 |
|
|
| 16-18 | Уравнения с модулями. Раскрытие модулей – стандартные схемы. Метод интервалов при раскрытии модулей. | 3 |
|
|
| 19-20 | Неравенства с двумя переменными. Множества решений на координатной плоскости. Стандартные неравенства. Метод областей. | 2 |
|
|
| 21-23 | Неравенства с модулями. Простейшие неравенства. Схемы освобождения от модулей в неравенствах. | 3 |
|
|
| 24-25 | Эквивалентные замены разностей модулей в разложенных и дробных неравенствах («правило знаков»). | 2 |
|
|
|
| Рациональные алгебраические системы
| 10 |
|
|
| 26 | Уравнения с несколькими переменными. Рациональные уравнения с двумя переменными. Однородные уравнения с двумя переменными. | 1 |
|
|
| 27-28 | Рациональные алгебраические системы. Метод подстановки. Метод исключения переменной. Равносильные линейные преобразования систем. | 2 |
|
|
| 29-30 | Однородные системы уравнений с двумя переменными.
| 2 |
|
|
| 31 | Замена переменных в системах уравнений.
| 1 |
|
|
| 32-33 | Система Виета и симметрические системы с двумя переменными. | 2 |
|
|
| 34-35 | Сведение уравнений к системам.
| 2 |
|
|
Календарное поурочно-тематическое планирование элективного учебного предмета для учащихся 11 класса «Алгебра плюс: алгебра с точки зрения высшей математики».
1 час в неделю, всего 34 часа
| № урока |
Содержание программного материала | Кол-во часов | Сроки | Примечание |
|
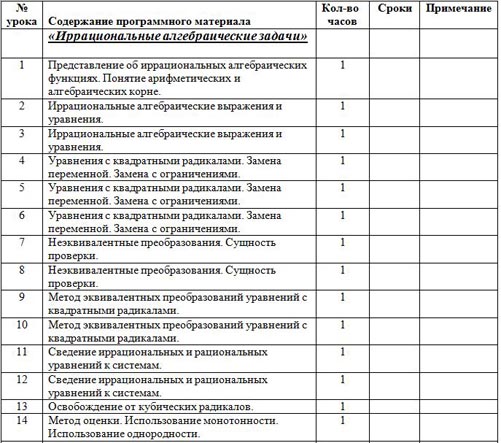
| «Иррациональные алгебраические задачи»
|
|
|
|
| 1 | Представление об иррациональных алгебраических функциях. Понятие арифметических и алгебраических корне. | 1
|
|
|
| 2 | Иррациональные алгебраические выражения и уравнения. | 1 |
|
|
| 3 | Иррациональные алгебраические выражения и уравнения. | 1 |
|
|
| 4 | Уравнения с квадратными радикалами. Замена переменной. Замена с ограничениями. | 1 |
|
|
| 5 | Уравнения с квадратными радикалами. Замена переменной. Замена с ограничениями. | 1 |
|
|
| 6 | Уравнения с квадратными радикалами. Замена переменной. Замена с ограничениями. | 1 |
|
|
| 7 | Неэквивалентные преобразования. Сущность проверки. | 1 |
|
|
| 8 | Неэквивалентные преобразования. Сущность проверки. | 1 |
|
|
| 9 | Метод эквивалентных преобразований уравнений с квадратными радикалами. | 1 |
|
|
| 10 | Метод эквивалентных преобразований уравнений с квадратными радикалами. | 1 |
|
|
| 11 | Сведение иррациональных и рациональных уравнений к системам. | 1 |
|
|
| 12 | Сведение иррациональных и рациональных уравнений к системам. | 1 |
|
|
| 13 | Освобождение от кубических радикалов. | 1 |
|
|
| 14 | Метод оценки. Использование монотонности. Использование однородности. | 1 |
|
|
| 15 | Метод оценки. Использование монотонности. Использование однородности. | 1 |
|
|
| 16 | Иррациональные алгебраические неравенства. Почему неравенства с радикалами сложнее уравнений. | 1 |
|
|
| 17 | Иррациональные алгебраические неравенства. Почему неравенства с радикалами сложнее уравнений. | 1 |
|
|
| 18 | Иррациональные алгебраические неравенства. Почему неравенства с радикалами сложнее уравнений. | 1 |
|
|
| 19 | Эквивалентные преобразования неравенств. Стандартные схемы освобождения от радикалов в неравенствах (сведения к системам и совокупностям систем). | 1 |
|
|
| 20 | Эквивалентные преобразования неравенств. Стандартные схемы освобождения от радикалов в неравенствах (сведения к системам и совокупностям систем). | 1 |
|
|
| 21 | «Дробно – иррациональные» неравенства. Сведения к совокупностям систем. | 1 |
|
|
| 22 | «Дробно – иррациональные» неравенства. Сведения к совокупностям систем. | 1 |
|
|
| 23 | «Дробно – иррациональные» неравенства. Сведения к совокупностям систем. | 1 |
|
|
| 24 | Метод интервалов при решении иррациональных неравенств. | 1 |
|
|
| 25 | Метод интервалов при решении иррациональных неравенств. | 1 |
|
|
| 26 | Метод интервалов при решении иррациональных неравенств. | 1 |
|
|
| 27 | Замена при решении иррациональных неравенств. | 1 |
|
|
| 28 | Замена при решении иррациональных неравенств. | 1 |
|
|
| 29 | Использование монотонности и оценок при решении неравенств. | 1 |
|
|
| 30 | Использование монотонности и оценок при решении неравенств. | 1 |
|
|
| 31 | Иррациональные алгебраические системы. Основные приёмы. | 1 |
|
|
| 32 | Иррациональные алгебраические системы. Основные приёмы. | 1 |
|
|
| 33 | Смешанные системы с двумя переменными. Иррациональные уравнения с модулями и параметрами. | 1 |
|
|
| 34 | Смешанные системы с двумя переменными. Иррациональные уравнения с модулями и параметрами. | 1 |
|
|
Требования к уровню подготовки выпускников
В результате изучения курса «Алгебра плюс: элементарная алгебра с точки зрения высшей математики» учащиеся должны:
| Элементы содержания | Знать | Уметь |
| Рациональные алгебраические уравнения и неравенства
| Знать основные принципы и методы решения алгебраических уравнений. Знать общую схему решения дробно-рациональных уравнений. Знать метод интервалов и метод оценки. Понимать нестандартные формулировки задачи. | Уметь решать дробно-рациональные уравнения. Уметь применять эти методы для решения дробно-рациональных неравенств. Уметь решать нестандартные по формулировке задачи |
| Рациональные алгебраические системы | | |
| Иррациональные алгебраические задачи | | |
Для реализации содержания программы используется литература:
1) С.Н. Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин. Алгебра и начала
Учебник 10 класс. Москва «Просвещение» 2008 г.,Учебник 11 класс. Москва «Просвещение» 2009.
А.Ш. Алимов, Ю.М. Колягин Алгебра и начала анализа.Учебник 10-11 класс. Москва «Просвещение» 2007 г.
Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Конкурсные задачи по математике. М.: Наука, 1992.
4) Цыпкин А.Г. Справочник по математике для средних учебных заведений. – 3-е изд. – М.: Наука, 1983.
5) Шарыгин И.Ф. «Факультативный курс по математике. Решение задач», 10 кл. Москва, «Просвещение», 1989г.
6) И.Ф.Шарыгин, В.И.Голубев «Факультативный курс по математике. Решение задач», 11 кл., Москва, «Просвещение», 1991г.
7) М.Л.Галицкий, М.М Мошкович, С.И. Шварцбурд., «Углубленное изучение курса алгебры и математического анализа», Москва, «Просвещение», 1990г.
А также тренировочные материалы для подготовки к ЕГЭ.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа элективного курса по математике «Алгебра плюс: элементарная алгебра с точки зрения высшей математики» (26.5 КB)
Рабочая программа элективного курса по математике «Алгебра плюс: элементарная алгебра с точки зрения высшей математики» (26.5 КB)
 0
0 800
800 86
86 Нравится
0
Нравится
0


