Итоговый тест по математике, 7 класс

Итоговый тест по математике, 7 класс

Рейтинг формируется путём подсчёта общего количества баллов, полученных учащимися за выполнение первой и второй частей работы. За каждое верно решенное задание первой части учащемуся начисляется 1 балл. Во второй части работы около каждого задания указано количество баллов, которые засчитываются в рейтинговую оценку ученика при верном выполнении этого задания. Балл, приписанный каждому заданию, характеризует относительную сложность этого задания в работе.

Работа состоит из двух частей и содержит 11 заданий. На выполнение работы даётся 45 мин.

Для оценивания результатов выполнения работы применяются два количественных показателя: отметки «2», «3», «4», или «5» и рейтинг – сумма баллов за верно выполненные задания.

Оценка «2» выставляется, если ученик набрал менее 6 баллов. Отметка «3» выставляется за 6 - 8 баллов.

Отметка «4» выставляется, если набрано от 9 до 12 баллов.

Для получения отметки «5» необходимо набрать 13 - 16 баллов. С критериями оценивания и структурой работы необходимо ознакомить учащихся до проведения итоговой работы. Вариант 1

1. Упростите 5(2а + 1) – 3

Ответ:

1. Вынесите общий множитель за скобки 18а³  6а ²

Ответ:

_3⁴ _3  3⁴

1. Упростите выражение:

₃3 _{ 3}10

Ответ:

1. Упростите выражение ⁽х − 6⁾² − 2х(−3х − 6).

Ответ:

1. Решите уравнение: 5у + 2⁽3 − 4у⁾ = 2у + 21

Ответ:

1. Боковая сторона равнобедренного треугольника на 8 см меньше основания. Найдите стороны треугольника, если известен периметр треугольника 44 см.

Ответ:

1. Представьте многочлен в виде произведения Ответ:

х ²  ху  4х  4 у

1. Вычислите координаты точки пересечения прямых 2х + 3у = – 12 и 4х – 6у = 0

Ответ:

Часть 2.

1. (2 балла) Решите уравнение: (х  2)²  8х  (х 1)(х  1)

1. (3 балла) Решите систему уравнений:

^{2(3х  у)  5  2х  3у,}



_5  (х  2 у)  4 у  16.

1. (3 балла) Решите задачу:

Один из смежных углов в 2 раза больше другого. Найдите больший смежный угол.

7 класс

Вариант 2

1. Упростите 3(4х + 2) – 5

Ответ:

1. Вынесите общий множитель за скобки 8а ⁴  2а³

Ответ:

Упростите выражение: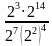

Ответ:

1. Упростите выражение ⁽а − 5⁾² − а(−10 − 2а)

Ответ:

1. Решите уравнение 3⁽2 − 3у⁾ + 5у = 2у − 6

Ответ:

1. Основание равнобедренного треугольника на 5 см больше боковой стороны. Найдите стороны треугольника, если известен периметр треугольника 35 см.

Ответ:

1. Представьте многочлен в виде произведения 2а  ас  2с  с ²

Ответ:

1. Вычислите координаты точек пересечения прямых х + 3у = – 12 и 4х – 6у = – 12

Ответ:

Часть 2.

1. (2 балла) Решите уравнение (х  3)²  х  (х  2)(2  х)

1. (3 балла) Решите систему уравнений:

1. (3 балла) Решите задачу:

^{2(3х  2 у)  9  4х  21,}



^2х  10  3  (6х  5 у).

Один из смежных углов в 4 раза больше другого. Найдите больший смежный угол.

Ответы

Вариант 1		Вариант 2
Часть 1
1	10а + 2		1	12х – 1
2	6а2(3а + 1)		2	2а3(4а + 1)
3	27		3	4
4	7х2 + 36		4	3а2 + 25
5	− 3		5	2
6	20 см, 12 см, 12 см		6	10 см, 10 см, 15 см
7	(х – у)(х – 4)		7	(2 – с)(а – с)
8	(– 3; – 2)		8	(– 6; – 2)
Часть 2
9	– 1,25		9	– 2,6
10	(– 7; 3)		10	(– 4; 5)
11	120⁰		11	144⁰

Решение второй части:

1. вариант

9. (х  2)²  8х  (х 1)(х  1) х² − 4х + 4 + 8х = х² − 1 4х = −5

х = −1,25. Ответ: −1,25



^{2(3х  у)  5  2х  3у,}

10.

_5  (х  2 у)  4 у  16.

� ,

6х − 2у − 5 = 2х − 3у 5 − х + 2у = 4у + 16

�

4х + у = 5

−х − 2у = 11^,

� ,

8х + 2у = 10

−х − 2у = 11 7х = 21

х = 3,

Если х = 3, то 4 ∙ 3 + у = 5

у = −7. Ответ: (– 7; 3)

11. Один из смежных углов в 2 раза больше другого. Найдите больший смежный угол.

Пусть градусная мера меньшего из углов равна х, тогда градусная мера большего равна 2х.

Сумма смежных углов равна 180^°.

х + 2х = 180^°

х = 60^°, Ответ: 120⁰

1. вариант

9. (х  3)²  х  (х  2)(2  х) х² + 6х + 9 − х = х² − 4 5х = −13

х = −2,6. Ответ: −2,6

10.

^{2(3х  2 у)  9  4х  21,}



^2х  10  3  (6х  5 у).

� ,

6х + 4у + 9 = 4х + 21

2х + 10 = 3 − 6х − 5у

� ,

2х + 4у = 12

8х + 5у = −7

�

−8х − 16у = −48 8х + 5у = −7 ^,

−11у = −55

у = 5,

Если у = 5, то 2х + 4 ∙ 5 = 12

х = −4. Ответ: (– 4; 5)

11. Один из смежных углов в 4 раза больше другого. Найдите больший смежный угол.

Пусть градусная мера меньшего из углов равна х, тогда градусная мера большего равна 4х.

Сумма смежных углов равна 180^°.

х + 4х = 180^°

х = 36^°, Ответ: 144⁰