Открытый урок по информатике
На тему
Двоичная арифметика
Предмет: Информатика
Учитель: Аюпова З.А
8 «Б»
19.10.2017г.
1 четверть
Раздел «Информация и информационные процессы»
Тема урока: Двоичная арифметика
Цели обучения :
Образовательные:
познакомить учащихся с двоичной системой счисления, указать ее недостатки и преимущества использования в вычислительной технике;
Развивающие:
развивать логическое мышление; формировать навыки выполнения арифметических действий с двоичными числами;
Воспитательные:
прививать интерес к предмету.
Оборудование: компьютер, учебник, доска, мел.
План урока:
I. Организационный момент /3 мин/
II.Формативное оценивание Д/з/7 мин/
III. Закрепление знаний и умений /20 мин/
IV. Выставление оценок. Рефлексия /7 мин/
V. Домашнее задание /3 мин/
Ход урока:
Организационный момент
Приветствие, проверка отсутствующих.
Постановка целей урока
Формативное оценивание Д/з
Системой счисления называется совокупность набора специальных знаков (цифр) и правил для записи чисел
Перевести число 1101 (2) в десятичную систему счисления
_____________________________________________________________________________
_____________________________________________________________________________
Перевести число 17 (8) в десятичную систему счисления
_____________________________________________________________________________
_____________________________________________________________________________
Расположить числа в порядке возрастания.
1112 А216, 7610 17 (8)
___________________________________________________________________________
___________________________________________________________________________
___________________________________________________________________________
___________________________________________________________________________
Закрепление знаний и умений
После предложенных ответов учащихся, комментирую и объясняю, что сегодня на уроке мы научимся правильно выполнять арифметические действия в двоичной системе счисления.
Двоичная система счисления издавна была предметом пристального внимания многих учёных. П.С.Лаплас писал о своём отношении к двоичной (бинарной) системе счисления великого математика Г.Ф.Лейбница: «В своей бинарной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль – небытие и что высшее существо создает всё из небытия точно таким же образом, как единица и нуль в его системе выражают все числа ». Эти слова подчеркивают удивительную универсальность алфавита состоящего всего из двух символов.
Двоичная арифметика.
Для того чтобы лучше освоить двоичную систему счисления, необходимо освоить выполнение арифметических действий над двоичными числами.
Сложение.
Таблица сложения двоичных чисел проста.
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
1 + 1 + 1 = 11
При сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания.
Вычитание.
0 – 0 = 0
0 – 1 = 11
1 – 0 = 1
1 – 1 = 0
Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведённой таблицей вычитания с учетом возможных заёмов из старших разрядов.
Пример.

Умножение.
Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя.
Пример.
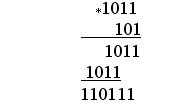
Деление.
При делении столбиком приходится в качестве промежуточных результатов выполнять действия умножения и вычитания.
Пример.
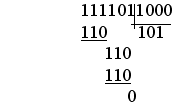
III. Закрепление знаний и умений
Решите задачи.
Выполните сложение:
1001001 + 10101 (ответ 1011110);
101101 + 1101101 (ответ 10011010)
11000,11 + 11010,11 (ответ 110011,1)
Выполните вычитание:
10001000 – 1110011 (ответ 10101)
1101100 – 10110110 (ответ – 1001010)
110101,101 – 1001,111 (101011,11)
Выполните умножение:
100001*111,11 (ответ: 11111111,11)
10011*1111,01 (ответ: 100100001,11)
Выполните деление:
1000000 / 1110 (ответ:100)
11101001000/111100 (ответ: 11111)
Решение примеров на системы исчислений:
| 1. Переведите из двоичной системы в десятичную, восьмеричную и шестнадцатеричную системы: | |
| А) 1011001 Б) 111000 В) 11101101 Г) 1000011 | А) 111111 Б) 1001001 В) 11100111 Г) 100110101 |
| 2. Переведите из шестнадцатеричной системы в десятичную: | |
| А) 9ЕА Б) F8B В) 185 | А) 288 Б) С8Е В) А3D |
| 3. Переведите из восьмеричной системы в десятичную: | |
| А) 222 Б) 324 В) 155 | А) 777 Б) 665 В) 245 |
| 4. Переведите из десятичной системы в восьмеричную и шестнадцатеричную: | |
| А) 311 Б) 515 В) 2433 | А) 488 Б) 1048 В) 685 |
| 5. Двоичная арифметика: | |
| А) 101101+10011 Б) 101101+110010 В) 110001 – 11101 Г) 11100-1011 | А) 110101 + 10111 Б) 110111 + 101011 В) 101101 – 10111 Г) 100100 - 11011 |
Тема « Система счисления»- одна из традиционных в курсе информатике. Являясь смежной с темами курса математики она вносит вклад и в математическое образование.
Но как показывает практика данная тема остается одной из самых трудных для понимания в школьном курсе информатике. Чтобы заинтересовать учеников можно использовать такую форму деятельности учащихся как графическая работа.
Суть работы заключается в следующем. Вам будут розданы карточки где
каждая координата точки записана в двоичной системе координат. Вам надо перевести координаты точек в десятичную систему счисления и, применяя знания по математике, построить точки в программе MICROSOFT EXCEL.
Нарисуйте фигуру
Каждой группе выдается карточка, содержащая таблицу с координатами точек, записанными в двоичной системе счисления, и система координат. Для выполнения задания необходимо:
а) перевести координаты точек в десятичную систему;
б) проверить правильность с помощью программы Калькулятор (этот пункт при желании можно пропустить);
в) построить по ним фигуру в координатной плоскости по вариантам:
Для выполнения этого задания вам понадобятся не только знания, полученные сегодня на уроке, но и математические знания. Каждому ученику выдается тетрадный лист с нанесенной на нем системой координат (заранее подготавливается учителем) – .
Пояснение к заданию:
каждая координата точки записана в двоичной системе координат. Вам надо перевести координаты точек в десятичную систему счисления и, применяя знания по математике, построить точки на системе координат, соединить их.
I вариант (буква Г)
Отметьте и последовательно соедините на координатной плоскости точки, координаты которых приведены в двоичной системе счисления.
| № точки | Двоичный код | Десятичный код |
| 1 | (101;101) |
|
| 2 | (101;101000) |
|
| 3 | (11001;101000) |
|
| 4 | (11001;100011) |
|
| 5 | (1010;100011) |
|
| 6 | (1010;101) |
|
| 7 | (101;101) |
|
Ответ: (5;5), (5;40), (25;40), (25;35), (10;35), (10;5), (5;5).
I вариант. Звезда
| № точки | Двоичный код | Десятичный код |
| 1 | (10; 1111) |
|
| 2 | (1000; 10000) |
|
| 3 | (1011; 10110) |
|
| 4 | (1110; 10000) |
|
| 5 | (10100; 1111) |
|
| 6 | (10000; 1010) |
|
| 7 | (10010; 100) |
|
| 8 | (1011; 111) |
|
| 9 | (100; 100) |
|
| 10 | (110; 1010) |
|
| 11 | (10; 1111) |
|
Ответ: (2;15), (8;16), (11; 22), (14; 16), (20; 15), (16; 10), (18; 4), (11; 7), (4;4), (6;10), (2;15)
II вариант. Ракета
| № точки | Двоичный код | Десятичный код |
| 1 | (1000; 10) |
|
| 2 | (101; 10) |
|
| 3 | (1000; 1010) |
|
| 4 | (1000; 10101) |
|
| 5 | (1011; 11001) |
|
| 6 | (1110; 10101) |
|
| 7 | (1110; 1010) |
|
| 8 | (10001; 10) |
|
| 9 | (1110; 10) |
|
| 10 | (1110; 111) |
|
| 11 | (1100; 111) |
|
| 12 | (1101; 10) |
|
| 13 | (1001;10) |
|
| 14 | (1010; 111) |
|
| 15 | (1000; 111) |
|
| 16 | (1000; 10) |
|
Ответ: (8;2), (5;2), (8;10), (8;21),(11;25), (14;21), (14;10),(17;2),(14;2), (14;7), (12;7), (13;2), (9;2), (10;7), (8;7), (8;2).
Суммативное оценивание
IV. Выставление оценок. Рефлексия
| Рефлексия | «Светофор»
|
|
|
|
V. Домашнее задание
Выучить правила выполнения арифметических действий в двоичной системе счисления, а так же таблицы сложения, вычитания и умножения в двоичной системе счисления.
Стр.18 задания 1

 Получите свидетельство
Получите свидетельство Вход
Вход











 Двоичная арифметика (30.75 KB)
Двоичная арифметика (30.75 KB)
 0
0 1614
1614 48
48 Нравится
0
Нравится
0







