Посмотрите на следующие пять многогранников.

Они являются правильными, так как у каждого из них все грани – одинаковые правильные многоугольники, в каждой вершине одного многоугольника сходится одно и то же число рёбер, а соседние грани сходятся под равными углами.
Правильный тетраэдр – многогранник, составленный из 4 правильных треугольников.
Куб – многогранник, составленный из 6 квадратов.
Правильный октаэдр – многогранник, составленный из 8 правильных треугольников.
Правильный додекаэдр – многогранник, составленный из 12 правильных пятиугольников.
Правильный икосаэдр – многогранник, составленный из 20 правильных треугольников.
Давайте составим таблицу, в которую запишем число вершин, рёбер и граней у каждого многогранника. Затем для каждого многогранника найдём число, равное числу вершин плюс число граней минус число рёбер.
Тетраэдр. У него 4 вершины, 4 грани и 6 рёбер.
Куб. У него 8 вершин, 6 граней и 12 рёбер.
Октаэдр. У этого многогранника 6 вершин, 8 граней и 12 рёбер.
Додекаэдр. У него 20 вершин, 12 граней и 30 рёбер.
Икосаэдр. У этого многогранника 12 вершин, 20 граней и 30 рёбер.
Заполним последний столбец таблицы. Найдём число, равное числу вершин плюс число граней минус число рёбер.

Обратите внимание, что в последнем столбце таблицы для всех многогранников получился один и тот же результат – два.
Число вершин, граней и рёбер связано таким соотношением не только у правильных, но и у всех других многогранников. Вы можете проверить это для любых взятых наугад многогранников.
Это соотношение называется формулой Эйлера.

Его доказал математик Леонард Эйлер. Этот величайший учёный родился в Швейцарии, но почти полжизни провёл в России. Он внёс огромный вклад в становление русской науки. В 1750 году Леонард Эйлер установил связь между числом вершин, рёбер и граней для многогранников. Это заложило фундамент нового раздела математики – топологии.
Рассмотрим ещё одну особенность правильных многогранников.
Тетраэдр. Если центры его граней считать вершинами нового многогранника, то мы снова получим тетраэдр.

Теперь давайте сразу возьмём куб и октаэдр. Заметим, что если центры граней куба считать вершинами нового многогранника, то получим октаэдр, а если центры граней октаэдра считать вершинами нового многогранника, то получим куб.

Аналогично для додекаэдра и икосаэдра. Если центры граней додекаэдра считать вершинами нового многогранника, то получим икосаэдр, а если центры граней икосаэдра считать вершинами нового многогранника, то получим додекаэдр.

История правильных многогранников уходит в глубокую древность. Совершенные формы и математические закономерности, присущие правильным многогранникам, являлись причиной того, что им приписывались различные магические свойства. Все 5 геометрических фигур (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр) издавна были спутниками волшебников и звездочётов.
Сейчас вы видите развёртки эти многогранников.

Если вы потрудитесь над их изучением, то сможете изготовить модели многогранников из бумаги.
Если сделать такие модели из цветной бумаги, то у вас получатся геометрические игрушки, которые вы можете использовать как украшение для новогодней ёлки.

 Получите свидетельство
Получите свидетельство Вход
Вход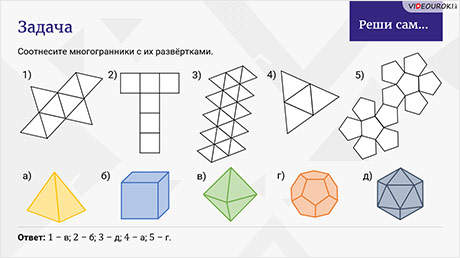




 9636
9636

