Геометрия – одна из самых древних наук, она возникла ещё до нашей эры. Слово «геометрия» в переводе с греческого означает «землемерие». Возникновение и развитие геометрии было связано с тем, что людям необходимо было выполнять различные измерительные работы при разметке земельных участков, проведении дорог, строительстве зданий и сооружений.
Считается, что истоки геометрии находились в Древнем Египте, ведь строительство храмов и пирамид требовало геометрических знаний, позволяющих выполнять сложные чертёжные и измерительные работы. Многочисленные памятники письменности свидетельствуют о том, что уже около 4000 лет назад египтяне имели большой запас геометрических сведений.
В начале VI в. до н. э. с развитием мореплавания и торговли накопленные египтянами знания о свойствах фигур стали достоянием учёных Древней Греции. Постепенно происходит переход от практической к теоретической геометрии. Огромный вклад в формирование геометрии внёс древнегреческий философ и математик Фалес.
Важную роль в развитии геометрии сыграл древнегреческий учёный Евклид, который жил в Александрии в III в. до н. э. Его заслуга состояла в том, что он систематизировал накопленный к тому времени богатый геометрический материал. Итогом геометрических исследований Евклида стал научный труд, состоящий из 13 книг, который называется «Начала».
Таким образом, геометрия возникла на основе практической деятельности людей, а в дальнейшем сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.
А сейчас давайте поговорим об инструментах, которые мы будем использовать, чтобы начертить какую-либо фигуру или измерить какие-либо величины.
Итак, линейка. С её помощью можно: проводить прямые линии, измерять отрезки, строить отрезки данной длины. Обратите внимание, что бывают линейки и без делений. С помощью такой линейки можно только проводить прямые линии.

Циркуль. С помощью циркуля можно строить окружности, сравнивать отрезки по величине, откладывать на прямой отрезки заданной длины.

Транспортир. Этот инструмент используют для измерения и построения углов.
Шкала транспортира – это полуокружность. Центр этой полуокружности
отмечен на транспортире чёрточкой. Будем называть его серединой транспортира. Штрихи
шкалы транспортира делят полуокружность на 180 частей. Одна часть называется
градусом. Следовательно, шкала транспортира содержит 180 градусов. Слово
«градус» заменяют знаком  .
.

При этом обратите внимание, что на транспортире две шкалы.
Если сторона угла совпадает с правой половиной основания транспортира, то используют внутреннюю шкалу, а если с левой, то – внешнюю.
Так, например, измерим вот такой угол.

Транспортир накладываем на угол так, чтобы вершина угла совпала с чёрточкой – серединой основания транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона укажет на величину угла в градусах.
Получается, что этот угол равен  .
.
Посмотрите, сторона угла совпала с правой половиной основания транспортира и для измерения угла мы использовали внутреннюю шкалу транспортира.
А теперь давайте с вами решим несколько задач, которые покажутся вам совсем непохожими, но каждая из них некоторым образом относится к геометрии.
Задача первая. Двенадцать спичек выложены так, как показано на рисунке:
а) уберите две спички так, чтобы образовалось два неравных квадрата;
б) переложите три спички так, чтобы образовалось три равных квадрата.
Решение.
а)

б)

Задача вторая. Разделите фигуру, изображённую на рисунке, на четыре равные части так, чтобы линия разреза шла по сторонам квадратов.

Решение.

Задача третья. Можно ли нарисовать фигуру, изображённую на рисунке, не отрывая карандаша от бумаги и не проводя более одного раза никакой линии?

Решение.

Решить эту задачу можно, если начать рисовать фигуру с любой вершины.

А теперь посмотрите на следующую фигуру (закрытый конверт).

На первый взгляд, она проще, так как содержит меньшее количество линий. Но решить для неё такую задачу, то есть нарисовать, не отрывая карандаша от бумаги и не проводя более одного раза никакой линии этой фигуры, мы не можем. Почему это нельзя сделать, а также как решать подобные задачи, мы узнаем на одном из наших следующих занятий.

 Получите свидетельство
Получите свидетельство Вход
Вход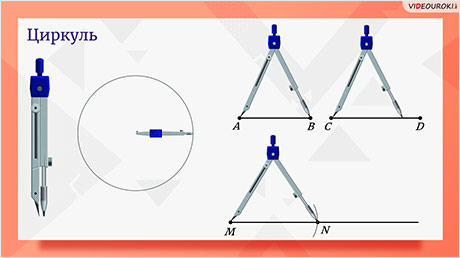




 11036
11036