Геометрия – это наука, которая занимается изучением геометрических фигур. Также она изучает форму и взаимное расположение фигур в пространстве.
Если посмотреть вокруг, то можем сказать, что мы живём в пространстве трёх измерений, то есть в трёхмерном пространстве.
Представьте, что перед вами стоит дом. Что можно о нём сказать?
В этом доме два подъезда. Он пятиэтажный.
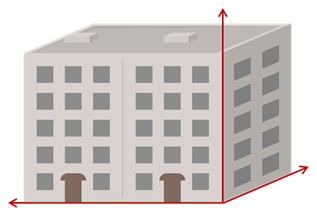
Мы можем сказать, что этот дом длиной в 2 подъезда, шириной в 2 окна и высотой в 5 этажей. Получается, чтобы представить дом, нам понадобилось задать три величины – длину, ширину и высоту. Эти три измерения мы с вами используем каждый день, говоря о предметах, которые нас окружают. Например, длина ленты, ширина окна, высота горы…
Все предметы в окружающем нас мире имеют три измерения, но далеко не у всех можно указать длину, ширину, высоту.
Теперь посмотрим на следующие предметы: коробка, брус, кирпич.
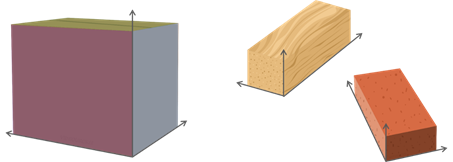
Все эти предметы имеют форму параллелепипеда. Но точнее, прямоугольного параллелепипеда, так как все грани являются прямоугольниками. У каждого из этих предметов можно указать длину, ширину и высоту. Многие окружающие нас предметы имеют форму параллелепипеда.
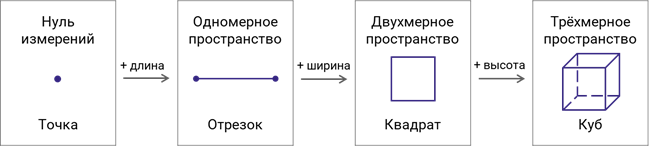
Прямоугольный параллелепипед – это геометрическое тело, которое полностью можно описать тремя измерениями – длиной, шириной и высотой. Можно сказать, что параллелепипед считается символом нашего пространства.
Отметим, что мы можем говорить о длине, ширине и высоте параллелепипеда, расположенного конкретным образом на земле (или на другой поверхности). Высотой в этом случае называют измерение, направленное вертикально вверх от земли. В случае, если мы не знаем, как расположен параллелепипед, говорить о длине, ширине и высоте не совсем верно.
А теперь представим, что высота исчезнет и останется два измерения – длина и ширина. Тогда весь мир станет плоским.
В математике говорят, что плоскость является двухмерным пространством. Плоскость представляется идеально ровной, гладкой и неограниченной во всех направлениях.

Например, гладкая поверхность стекла даёт представление о части плоскости. Здесь рассматриваются такие фигуры, как треугольник, квадрат, круг, прямоугольник.

Если мы уберём ещё одно измерение – ширину, то останется одномерное пространство с одним измерением – длиной. Этот мир полностью лежит на прямой. Прямая простирается неограниченно в обе стороны.

Туго натянутая нить даёт нам представление о части прямой. В одномерном пространстве рассматриваются такие фигуры, как луч, отрезок.

В геометрии существует фигура, которая не имеет измерений. Это точка. Точка является самой маленькой геометрической фигурой.

Сейчас посмотрите на схему, которая показывает, как с увеличением измерений изменяются и усложняются геометрические фигуры.
А теперь давайте поговорим об изображении объёмных тел на плоскости. Как, например, нарисовать улицу, убегающую вдаль, чтобы это выглядело как в реальности, чтобы чувствовалась глубина пространства.
Перспектива – техника изображения объёмных тел на плоскости. Она позволяет «обмануть» зрение. Хорошим примером является картина венгерского художника Виктора Вазарели «Изучение перспективы».

Посмотрите, на ней фигура чем дальше находится от нас, тем меньших размеров изображается. А все линии, уходящие вглубь, сходятся в одной точке.
Отметим, что кроме перспективы, есть и другие средства изображения трёхмерного пространства на плоскости.
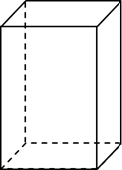
Посмотрите на прямоугольный параллелепипед.

Если бы мы не знали, что это прямоугольный параллелепипед, то не смогли бы понять, что находится за видимыми гранями этой фигуры. Поэтому, чтобы получить полное представление о том, какая фигура изображена, надо нарисовать то, что нам не видно, то, что находится за видимыми гранями.
И сделать мы бы это могли вот таким образом.
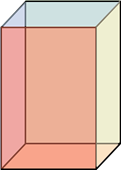
Но теперь стало непонятно, как по отношению к нам расположен этот параллелепипед: какие грани спереди, а какие – сзади. Чтобы получить полное представление об изображаемой фигуре и её расположении по отношению к нам, договорились те линии (рёбра), которые не видны, изображать пунктирными.
Сейчас посмотрите на четырёхугольник. У него четыре вершины и четыре стороны. Посмотрите на шестиугольник. У него шесть вершин и шесть сторон.

А теперь посмотрите на прямоугольный параллелепипед. У него восемь вершин и шесть граней.
Получается, что если известно число вершин у многоугольника, то сразу можно сказать, сколько у него сторон. А вот для объёмных тел (многогранников) это не так.
А теперь давайте с вами решим несколько задач.
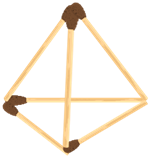
Задача первая. Из шести спичек составьте четыре треугольника со сторонами, равными длине спички.
Решение.
Задача вторая. Каким образом продавец тремя прямыми разрезами разделил головку сыра на восемь равных частей?
Решение.

Задача третья. Изобразите многогранник, у которого шесть вершин и шесть граней.
Решение.

Получили многогранник, у которого шесть вершин и шесть граней, – пирамиду, в основании которой лежит пятиугольник.

 Получите свидетельство
Получите свидетельство Вход
Вход




 7997
7997





