Давайте изобразим некоторую простую замкнутую ломаную линию. При этом звенья ломаной не должны пересекаться друг с другом. Эта ломаная разбивает всю плоскость на две части. Меньшая из двух частей плоскости ограничена нашей замкнутой ломаной. Большая часть простирается неограниченно.

Геометрическая фигура, которая состоит из простой замкнутой ломаной и части плоскости, ограниченной этой ломаной, называется многоугольником. Звенья ломаной называются сторонами многоугольника, а вершины ломаной – вершинами многоугольника.
Слово «многоугольник» указывает на то, что у фигуры много углов. Давайте посчитаем, сколько углов у данного многоугольника. У этого многоугольника 5 углов. Поэтому этот многоугольник называют пятиугольником.
Тогда если у многоугольника 6 углов, то его называют шестиугольником.
Многоугольник, у которого 4 угла, называют четырёхугольником, у которого 7 углов – семиугольником, у которого 9 углов – девятиугольником и так далее.
Обратите внимание, что у любого многоугольника вершин столько же, сколько и углов.
Сторон у многоугольника столько же, сколько и углов. Действительно, у пятиугольника – 5 сторон, у четырёхугольника – 4 стороны, у семиугольника – 7 сторон, а у девятиугольника – 9 сторон.
Самый простой многоугольник – это треугольник. Он состоит из 3 углов, 3 вершин и 3 сторон.
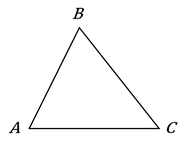
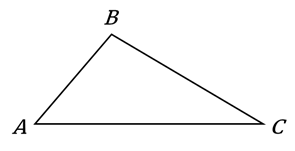
Вершины треугольника принято называть большими латинскими буквами. Обозначим вершины данного треугольника буквами А, B и C.
Для упрощения записи треугольник в математике обозначается значком
 и указанием
его вершин (
и указанием
его вершин ( ). Читается:
«треугольник
). Читается:
«треугольник 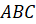 ».
».
Огромное семейство треугольников можно разделить на группы по числу равных сторон.
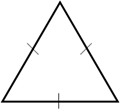
Итак, посмотрите на такой треугольник. У него нет равных сторон. В этом можно убедиться с помощью линейки. Треугольник, у которого нет равных сторон, называется разносторонним.
Посмотрите на следующий треугольник. У него 2 стороны равны. Это можно проверить с помощью линейки. Треугольник, у которого есть две равные стороны, называется равнобедренным.
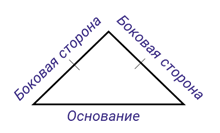
На рисунке равные стороны принято обозначать равным количеством чёрточек. Отметим, что равные стороны равнобедренного треугольника называют боковыми сторонами, а третью его сторону – основанием.
Теперь посмотрите на следующий треугольник. У него все 3 стороны равны. В этом можно убедиться с помощью линейки. Треугольник, у которого все 3 стороны равны между собой, называется равносторонним (или правильным).
Вы уже знаете, что углы бывают прямыми, острыми и тупыми.
Напомним, что прямой угол равен  . Если угол
меньше
. Если угол
меньше  , то его
называют острым. Если угол больше
, то его
называют острым. Если угол больше  , но меньше
, но меньше 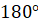 градусов, то
его называют тупым.
градусов, то
его называют тупым.
Тогда все треугольники можно разделить на группы в зависимости от величин углов.
Посмотрите на первый треугольник. У него все 3 угла меньше  , то есть
острые.
, то есть
острые.
Треугольник, у которого все углы острые, называется остроугольным.
Посмотрите на следующий треугольник.

У него 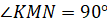 , то есть
прямой. Треугольник, у которого есть прямой угол, называется прямоугольным.
, то есть
прямой. Треугольник, у которого есть прямой угол, называется прямоугольным.
И ещё один треугольник.
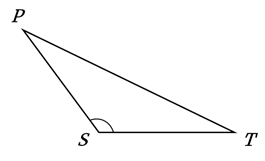
У него 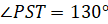 , то есть
тупой.
, то есть
тупой.
Треугольник, у которого есть тупой угол, называется тупоугольным.
Напомним, что углы треугольника можно измерить с помощью транспортира.
Измерим углы произвольного треугольника 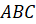 . У него
. У него  ,
, 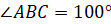 , а
, а  . Найдём сумму
этих углов. Она равна
. Найдём сумму
этих углов. Она равна 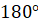 .
.
Запомните! Сумма углов треугольника
равна 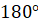 .
.
Соединяя треугольники друг с другом, можно образовывать другие фигуры.
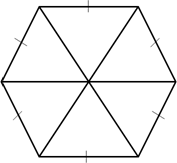
Возьмём, например, 6 правильных, то есть равносторонних, треугольников, которые имеют общую вершину. Они образуют шестиугольник, причём правильный, так как все его стороны равны между собой. Отметим, что шестиугольник является плоской фигурой, как и сам треугольник.
А вот если мы возьмём правильный треугольник и к его стороне приставим ещё 3 таких треугольника таким образом, чтобы у них одна вершина оказалась общей, то получим объёмное геометрическое тело. Это же пирамида.

При этом не забудем невидимую линию пирамиды изобразить пунктиром. Данная пирамида имеет 4 грани, 4 вершины и 6 рёбер. Её называют треугольной, так как боковые треугольники опираются на треугольник.
В зависимости от того, на какой многоугольник опираются треугольники, пирамиды бывают треугольные, четырёхугольные, пятиугольные и так далее. При этом многоугольник, на который опираются треугольники, в геометрии называется основанием пирамиды, а треугольники, которые опираются на основание, называются боковыми гранями.
Треугольную пирамиду также называют тетраэдром, что означает «четыре грани».
Сейчас давайте возьмём треугольную, четырёхугольную и пятиугольную пирамиды и разрежем их по рёбрам боковых граней.

Тогда мы получим фигуры, которые называются развёртками этих пирамид.

Треугольник лежит в основе разнообразных строительных и архитектурных сооружений. Роль треугольника в строительстве очень велика, так как он обладает важным свойством, которое называется жёсткостью. Оно состоит в следующем. Если взять три рейки и соединить их попарно, то получится треугольник, изменить форму которого можно, лишь сломав рейку.

Теперь мы с вами рассмотрим три основные задачи на построение треугольников, если заданы: две стороны и угол между ними; сторона и два прилежащих к ней угла; три стороны.
Построим треугольник по двум сторонам и углу между ними.
В  сторона
сторона 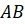 равна 4 см, сторона
равна 4 см, сторона 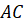 равна 6 см,
а угол между ними
равна 6 см,
а угол между ними 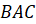 равен
равен  . Постройте
по этим данным треугольник
. Постройте
по этим данным треугольник  .
.
В первую очередь построим угол, равный  . Для этого
отметим произвольную точку и начертим луч с началом в этой точке. Теперь
наложим транспортир так, чтобы его середина совпала с началом луча, а луч
прошёл через начало отсчёта на шкале. На этой шкале найдём штрих, который
соответствует
. Для этого
отметим произвольную точку и начертим луч с началом в этой точке. Теперь
наложим транспортир так, чтобы его середина совпала с началом луча, а луч
прошёл через начало отсчёта на шкале. На этой шкале найдём штрих, который
соответствует  , и проведём
луч через этот штрих. Вершину угла обозначим буквой
, и проведём
луч через этот штрих. Вершину угла обозначим буквой 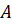 .
.
Теперь на одной стороне угла отложим отрезок 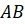 , равный 4
см, а на другой – отрезок
, равный 4
см, а на другой – отрезок 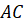 , равный 6
см. Затем проведём отрезок
, равный 6
см. Затем проведём отрезок  . Таким
образом,
. Таким
образом,  построен.
построен.
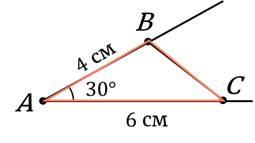
Отметим, что по двум сторонам и углу между ними можно построить единственный треугольник.
Построим треугольник по стороне и двум углам. В  сторона
сторона 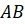 равна 5 см,
угол
равна 5 см,
угол 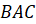 равен
равен  , угол
, угол 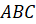 равен
равен 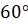 . Постройте
по этим данным т
. Постройте
по этим данным т .
.
Проведём прямую, на которой отложим отрезок 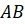 , равный 5
см. Теперь с помощью транспортира построим угол с вершиной в точке
, равный 5
см. Теперь с помощью транспортира построим угол с вершиной в точке 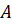 , равный
, равный 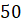 , и стороной,
лежащей на данной прямой. Затем построим угол с вершиной в точке
, и стороной,
лежащей на данной прямой. Затем построим угол с вершиной в точке 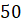 , равный
, равный 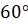 , и стороной,
лежащей на данной прямой. Точку пересечения других сторон углов обозначим
буквой
, и стороной,
лежащей на данной прямой. Точку пересечения других сторон углов обозначим
буквой 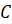 . Это и есть
третья вершина треугольника. Вот таким образом
. Это и есть
третья вершина треугольника. Вот таким образом  построен.
построен.

Отметим, что по стороне и двум прилежащим к ней углам можно
построить единственный треугольник, но при этом величины заданных углов не
могут быть произвольными. Позже вы узнаете, что такое построение возможно, если
сумма заданных углов меньше 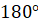 .
.
И построим треугольник по трём сторонам. В  сторона
сторона 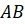 равна 4 см,
сторона
равна 4 см,
сторона  равна 3 см,
сторона
равна 3 см,
сторона 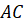 равна 2 см.
Постройте по этим данным
равна 2 см.
Постройте по этим данным  .
.
Проведём прямую, на которой отложим отрезок 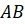 , равный 4
см. Теперь с помощью циркуля построим окружность с центром в точке
, равный 4
см. Теперь с помощью циркуля построим окружность с центром в точке 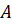 и радиусом 2
сантиметра. Построим окружность с центром в точке
и радиусом 2
сантиметра. Построим окружность с центром в точке 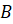 и радиусом 3
см. Точку пересечения этих окружностей обозначим буквой
и радиусом 3
см. Точку пересечения этих окружностей обозначим буквой 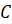 . Обратите
внимание, что мы можем выбрать любую из двух точек пересечения окружностей, так
как получающиеся треугольники равны. Соединим точки
. Обратите
внимание, что мы можем выбрать любую из двух точек пересечения окружностей, так
как получающиеся треугольники равны. Соединим точки 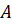 и
и 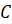 ,
, 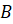 и
и 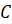 и получим
искомый
и получим
искомый  .
.

Отметим, что по трём сторонам можно построить единственный треугольник. При этом важно знать, что три данных отрезка могут служить сторонами треугольника, если сумма длин двух меньших отрезков больше длины наибольшего из них.

 Получите свидетельство
Получите свидетельство Вход
Вход




 4451
4451