Задачи на разрезание и складывание фигур

«Семь раз отмерь, один раз отрежь!» Эта пословица предостерегает вас от поспешности в решении задач на разрезание.

Задачами на разрезание увлекались многие учёные с древнейших времён. Решения многих простых задач на разрезание были найдены ещё древними греками, китайцами, но первое научное сочинение на эту тему принадлежит перу Абул-Вефа, знаменитого персидского астронома X века, жившего в Багдаде.

Всерьёз геометры занялись решением задач на разрезание фигур на наименьшее число частей и последующее составление из них фигур лишь в начале XX века.

Одним из основоположников этого увлекательного раздела геометрии был знаменитый составитель головоломок Генри Эрнест Дьюдени. Свои первые небольшие задачи он начал публиковать в различных журналах. А в 1907 году вышла в свет его первая книга «Кентерберийские головоломки», которая впоследствии неоднократно переиздавалась.

Задачи на разрезание увлекательны прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берётся за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению.

Задача первая. На рисунке изображён квадрат со стороной в 4 клетки. Разделите квадрат на 2 равные части так, чтобы линия разреза шла по сторонам клеток. Способы разрезания квадрата на 2 части будем считать различными, если части квадрата, полученные при одном способе разрезания, не равны частям, полученным при другом способе. Сколько всего решений имеет задача?

Решение.

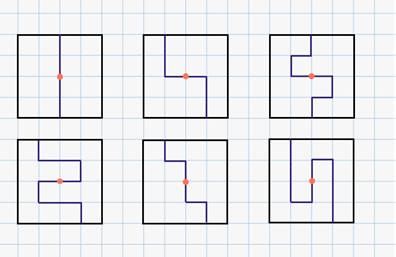
Отметим, что задача на разрезание на две или несколько одинаковых частей решена верно, если эти части можно наложить одна на другую так, что они совпадут (при этом разрешается наложить их наизнанку).

Квадрат можно разделить на две равные части и вот таким способом…

Но это решение и наше второе решение одинаковы, так как полученные в них фигуры можно совместить наложением, если повернуть один из квадратов на .

Ответ: 6.

Задача вторая. Разделите квадрат размером  клетки на 4 равные части так, чтобы линия разреза шла по сторонам клеток. Сколько всего решений имеет задача?

Решение.

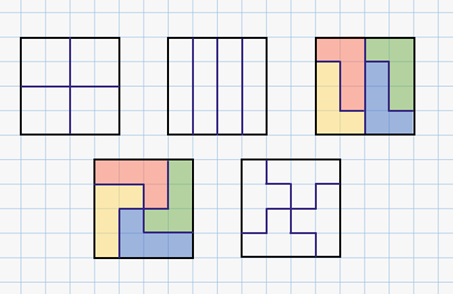
Обратите внимание на третий и четвёртый способы. Эти два способа различны, но части, на которые разрезается квадрат такими способами, одинаковые.

Ответ: 5.

Задача третья. Разделите фигуры, изображённые на рисунке, на 2 равные части. Разрезать можно не только по линиям клеток, но и по их диагоналям.

Решение.

На одном из предыдущих занятий мы с вами познакомились с игрой, которая называется пентамино. Эта игра была придумана в -x гг. XX в. американским математиком Соломоном Голомбом. Она быстро увлекла не только школьников и студентов, но и профессоров математики. Набор пентамино содержит 12 фигурок, каждая из которых составлена из 5 одинаковых квадратов, причём квадраты «соседствуют» друг с другом только сторонами. «Пента» в переводе с греческого означает «пять».

Все элементы этой игры обозначаются латинскими буквами, форму которых они напоминают.

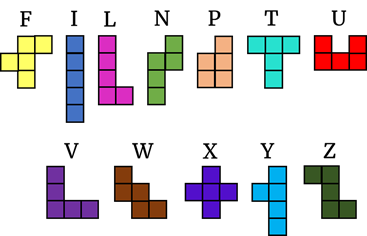
Из 12 фигур пентамино сложим прямоугольник размером . Фигурки пентамино можно переворачивать. Сейчас на рисунке вы видите один из возможных вариантов решения данной задачи.

Эту задачу впервые в 1965 году решил Джон Флетчер. Существует ровно 2339 различных укладок пентамино в прямоугольник такого размера, не считая повороты и отражения целого прямоугольника. Вы можете изготовить из картона набор пентамино и попробовать найти другие решения этой задачи.

Ранее мы уже говорили, что задача на сложение прямоугольника из всех фигурок пентамино без перекрытий и зазоров является очень распространённой. Каждый из 12 элементов игры состоит из 5 квадратов, а значит, прямоугольник должен получиться площадью 60 единичных квадратов.

Возможны прямоугольники размером  (выше мы уже сложили один из таких), ,  и .

На следующем слайде вы видите прямоугольники этих размеров, сложенные из фигур пентамино.

Отметим, что для прямоугольника размером  существует 1010 решений. Для прямоугольника размером  – 368 решений. Для прямоугольника размером  – всего 2 решения.

Прямоугольники размером и  составить нельзя, так как большинство фигур не поместятся по ширине.

Также на одном из предыдущих занятий мы с вами познакомились с паркетом, который был составлен из элемента пентамино в форме буквы Т. Из других фигур пентамино также можно составить паркеты.

В пентамино можно играть и вдвоём следующим образом. Двое игроков по очереди выбирают 1 из 12 фигур и располагают её на свободных клетках квадратного поля размером . Проигрывает тот, кто первым не сможет разместить на поле ни одного пентамино. А если всё же фигурки удалось разместить на доске, то выигрывает человек, который ходил последним.

Поле размером  полностью нельзя покрыть 12 элементами игры. Это поле состоит из 64 клеток, а значит, останется 4 свободные клетки. А вот если вырезать из середины квадрат из 4 клеток, то оставшиеся 60 клеток покрываются 12 фигурками пентамино. На данном рисунке изображено покрытие, которое предложил Голомб.

Сейчас вы видите ещё один вариант покрытия квадрата размером восемь на восемь с вырезанной серединой.

Вы тоже можете попробовать найти хотя бы один вариант покрытия такой фигуры.

Решим ещё одну задачу. 12 фигур пентамино уложены в коробку размером  так, как показано на рисунке. Попробуйте разместить ещё один комплект пентамино на оставшемся свободном поле.

Вот таким образом можно заполнить свободное поле ещё одним комплектом пентамино.