Посмотрите на фигуры, которые изображены на рисунке.

Это не квадраты, не прямоугольники… Как можно описать эти фигуры человеку, который их не видит?
Первая фигура похожа на букву Н. Можно сказать, что это буква Н с двумя перекладинами.
А что можно сказать про вторую фигуру?
Вторая фигура похожа на букву Г. Точнее, это буква Г, лежащая на боку.
А теперь опишите фигуру, изображённую на следующем рисунке. Это буква ТЭ.
Сейчас мы с вами приступим к выполнению заданий и будем называть эту фигуру буквой Т.
Задание первое. Раскрасьте фигуру, изображённую на рисунке а, буквами Т такой формы, как на рисунке б.
Отметим, что при выполнении этого задания букву Т можно поворачивать как угодно.
Решение. Буква Т состоит из 5 клеток.

Задание второе. Имеется лист клетчатой
бумаги размером  клеток.
Вырежьте из него как можно больше букв Т такой формы, как показано на рисунке.
клеток.
Вырежьте из него как можно больше букв Т такой формы, как показано на рисунке.
Решение. Начнём вырезать фигуры в виде буквы Т из верхнего левого угла листа бумаги.

Так, из листа бумаги мы смогли вырезать 16 фигур в форме буквы Т.
Задание третье. Можно ли завернуть куб в букву Т в один слой? Если можно, то изобразите эту букву. Укажите её размеры, если ребро куба равно 1у см.
Решение. В «букву Т» получится в один
слой завернуть куб с длиной ребра, равной  см.
см.

Теперь вы можете выполнить вот такое задание. Составьте конструкцию из трёх-четырёх букв Т и, не показывая её соседу по парте, словесно опишите её. Вам нужно описать фигуру так, чтобы ваш приятель смог её нарисовать. Если получилось, поменяйтесь ролями: теперь он объясняет, а вы рисуете.
А сейчас посмотрите на лебедей, которых изобразил голландский художник Мауриц Эшер.

Они образуют, как говорят математики, «паркет». Здесь каждая птица плотно прилегает к своим соседям без малейших зазоров, совсем как плашки паркетного пола. Правильным называется такой паркет, который составлен повторением одной и той же фигуры. Например, на следующем рисунке круги не образуют паркета, а зелёные и красные фигуры образуют.

Паркеты могут получаться и при соединении различных фигур. На данном рисунке – два квадрата разных размеров.

А вот если не обращать внимание на окраску, то можно заметить, что на самом деле этот паркет составлен вот из таких фигур…

Из фигур в форме буквы Т тоже можно составить паркет. Посмотрите, здесь каждая фигура плотно прилегает к соседним. Причём этот паркет является правильным, так как он представляет собой повторение одной и той же фигуры. При этом обратите внимание, что буква Т состоит из 5 равных квадратов. Такую фигуру называют пентамино.

Пентамино – пятиклеточные полимино, то есть плоские фигуры, каждая из которых состоит из 5 одинаковых квадратов, соединённых между собой сторонами.
Также этим словом называют очень известную логическую игру и головоломку одновременно. Она прекрасно тренирует геометрическое воображение у детей и взрослых. Элементами в этой игре являются плоские фигуры, каждая из которых состоит их 5 одинаковых квадратов. Всего существует 12 элементов пентамино. Все элементы обозначаются латинскими буквами, форму которых они напоминают.
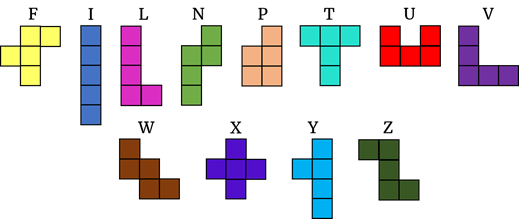
Видим, что фигура в форме буквы Т, состоящая из 5 одинаковых квадратов, является элементом этой игры.
При решении задач и головоломок фигурки можно вертеть и переворачивать, поэтому при изготовлении игры своими руками элементы надо делать двухсторонними (то есть закрашивать с двух сторон).
Посмотрите, следующие фигуры сложены из элементов пентамино.

Давайте рассмотрим решение самой распространённой задачи. Необходимо сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Так как каждая фигура состоит из 5 квадратов, то прямоугольник должен быть площадью 12 умножить на 5, то есть 60 единичных квадратов.
В таком случае возможны прямоугольники размером  ,
,  ,
,  и
и  .
.
Важно отметить, что прямоугольники размером  и
и  составить
из пентамино не получится, так как многие фигуры просто не поместятся по
ширине.
составить
из пентамино не получится, так как многие фигуры просто не поместятся по
ширине.
В прямоугольник размером  мы
можем уложить пентамино вот таким образом.
мы
можем уложить пентамино вот таким образом.

Существует ещё 1 способ укладки прямоугольника такого размера.
А вот для прямоугольника размером  существует
2339
существует
2339 различных
способов. Посмотрите на один из них.
различных
способов. Посмотрите на один из них.

Для прямоугольника размером  существует
1010 решений. Вот одно из них.
существует
1010 решений. Вот одно из них.

Для прямоугольника размером  – 368 решений. Вы видите одно из них.
– 368 решений. Вы видите одно из них.


 Получите свидетельство
Получите свидетельство Вход
Вход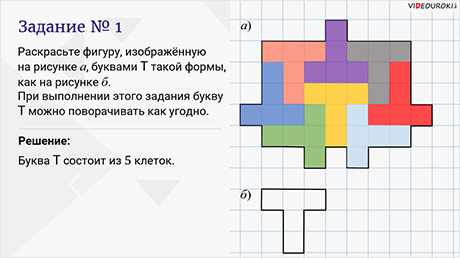




 13590
13590