Степень числа

Представим себе такую историю…

– И что это за число-то такое? – не мог понять Саша.

– Что случилось? – поинтересовался у друга Паша.

– Недавно я услышал, что человек состоит из клеток. И вот мне стало интересно, что это за клетки такие и сколько их в нашем теле.

– Это на самом деле интересно! – воскликнул Паша. – Расскажешь, что ты уже узнал?

– Все мы состоим из крошечных клеток, – начал Саша. – Это такие маленькие кирпичики, из которых построено всё наше тело. Они настолько мелкие, что увидеть их можно лишь в микроскоп.

Клетки обладают всеми признаками живого. Они способны размножаться, расти, обмениваться веществами и энергией с окружающей средой, реагировать на изменения, происходящие в этой среде.

– А сколько клеток в нашем теле? – спросил Паша.

– В энциклопедии я прочитал, что клеток в нашем теле вот такое число 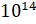, – расстроенно сказал Саша. – Но вот только я не понимаю, что это за число такое…10…а 14 к чему? И почему 14 такое маленькое?

– Давай спросим у Электроши, – предложил Паша. – Он точно всё знает.

– Ребята, прежде чем я вам расскажу о подобных числах, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь вернёмся к вашему вопросу, – продолжил Электроша. – Как вы знаете, сумму нескольких равных слагаемых удобно записывать с помощью произведения. Вот, например, 10 + 10 + 10 + 10 + 10 записывают короче: .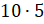

Для произведения, в котором все множители равны, математики тоже придумали способ, с помощью которого такое произведение можно записать короче. Вот вы не могли расшифровать число, обозначающее количество клеток в теле человека. А эта запись обозначает произведение.

– Произведение? – удивились мальчишки.

– Да! Произведение! А точнее говоря, эта запись означает, что нужно .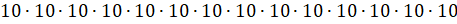

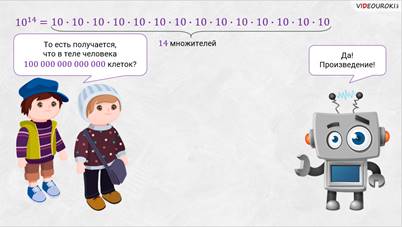
– То есть получается, что в теле человека 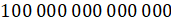клеток? – посчитали мальчишки.

– Получается так! – улыбнулся Электроша. – Кстати, такой способ записи произведения одинаковых множителей придумали давным-давно. Ещё в Древнем Египте учёные обратили внимание на то, что когда нужно выполнить умножение какого-либо числа на себя много раз, то на это тратится огромное количество ненужных усилий. Более того, такая операция ещё и вела к значительным финансовым затратам. Согласно действовавшим тогда установкам на оформление любых записей, каждое действие с числом должно было подробно описываться.

Самый простейший папирус тогда стоил весьма внушительную сумму денег. Вот умным египтянам и пришлось искать выход из сложившейся ситуации. Конечно, впоследствии ещё не один математик внёс усовершенствование в данный способ написания подобного произведения.

– Понятно! Такая запись обозначает произведение. Правильно? – спросили ребята.

– Не просто произведение, а произведение нескольких одинаковых множителей. –––––– Запомните! Выражение 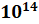называют степенью и читают «десять в пятой степени» или «пятая степень числа десять».

Обратите внимание: в записи степени участвуют два числа. Число, которое возводится в степень, называют основанием степени. В нашем случае это число 10. Другое число называют показателем степени. В нашем случае это 14. Число 14 показывает, сколько множителей, каждый из которых равен десяти, содержит произведение. Само же действие называют возведением в степень.

– Давайте попробуем прочитать следующие выражения: 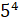, , 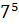, , 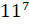, , 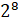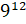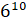– предложил Электроша.

– В первой строчке записаны «пять в четвёртой степени», «семь в пятой степени» и «одиннадцать в седьмой степени», – начал Паша.

– Во второй строчке – «восьмая степень числа два», «двенадцатая степень числа девять» и «десятая степень числа шесть», – продолжил Саша.

– Запомните! – сказал Электроша. –  Степенью числа a с натуральным показателем 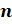, большим единицы называется произведение эн одинаковых множителей, каждый из которых равен числу a.

В общем виде степень с основанием a и показателем 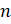 записывают так: .

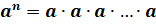Читают такую запись: «а в степени эн» или «эн-ая степень числа а».

– Электроша, вот ты в определении говоришь, что натуральный показатель больший единицы, – решили уточнить ребята. – А что, показатель степени не может быть равным единице?

– Может, – ответил Электроша, – но это один из особых случаев степени. Давайте порассуждаем. Если показатель степени равен единице, то что это значит?

– Это значит, что основание степени надо взять множителем один раз, – ответили мальчишки.

– Хорошо! Но как это представить? Взяли основание, а второго множителя нет. Так получается?

– Ну да, – задумались мальчишки.

– Поскольку в математике не принято рассматривать произведение, состоящее из одного множителя, то договорились, что 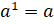, – продолжил Электроша. Вообще первая степень любого числа равна этому числу. Например, 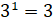, а .

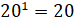– Электроша, ты сказал, что показатель степени равный единице – это один из особых случаев. А какие ещё есть особые случаи? – спросили ребята.

– Запомните! – начал Электроша. – Любое число в нулевой степени равно единице.

Ноль в любой натуральной степени равен нулю. А вот выражение ноль в нулевой степени считают не имеющим смысла.

 Единица в любой степени равна единице.

– А теперь прочитайте вот такие выражения: 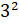, , 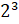– предложил Электроша.

– В первом случае записано «три во второй степени», – начал Паша.

– А во втором – «два в третьей степени», – продолжил Саша.

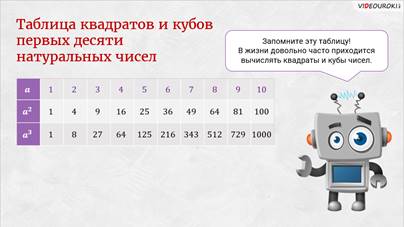
– Молодцы! – похвалил ребят Электроша. – Но часто в жизни вы можете услышать и другие, особые названия второй и третьей степени числа. Вторую степень числа чаще называют квадратом числа. Третью степень числа называют кубом числа. Тогда наше первое выражение можно ещё прочитать как «три в квадрате». А второе можно прочитать как «два в кубе».

На экране вы видите таблицу квадратов и кубов первых десяти натуральных чисел. Запомнив эту таблицу, вы сильно облегчите себе жизнь в будущем. Ведь в жизни довольно часто нам приходится вычислять квадраты и кубы чисел.

– А теперь давайте найдём значение следующего выражения: 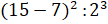– предложил Электроша.

– Электроша, а как выполнять вычисления, когда в выражениях есть степень? – задумались ребята. – Раньше у нас всё было просто: выполняли действия в скобках, потом умножение и деление, если они присутствовали в выражениях, а потом сложение и вычитание.

– Возведение числа в степень – это пятое арифметическое действие, – начал Электроша. Запомните! В выражениях со степенями, не содержащими скобки, сначала выполняют возведение в степень, затем умножение и деление, а в конце сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

– Теперь понятно! – обрадовались мальчишки. – В нашем выражении есть скобки. Значит, первым выполним действие в скобках. У нас вычитание. 15 – 7 = 8. Затем выполним действия со степенями. 8² = 64. А 2³ = 8. Осталось выполнить деление. 64 : 8 = 8.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: возведите в степень:

а) ;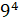

б) ;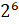

в) .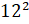

Решение: первое выражение девять в четвёртой степени. Нужно 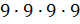. Получим 6561.

Следующее выражение два в шестой степени. Нужно 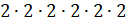. Получим 64.

И последнее выражение двенадцать в квадрате. Мы должны 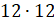. Получим 144.

Следующее задание: в каждый из овалов впишите значение выражения 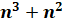при значении буквы 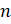, указанном в соответствующем уголке фигуры.

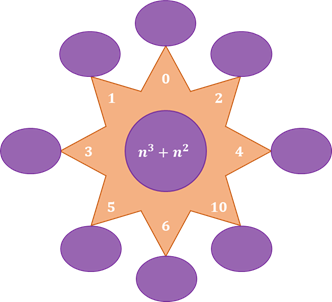
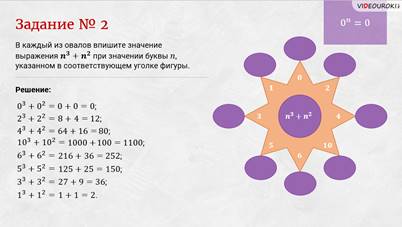
Решение: первое число 0. Подставим его в выражение 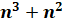. Мы помним, что ноль в любой степени равен нулю. Тогда 0 + 0 = 0.

Следующее число 2. Подставим его в наше выражение. Получим 2³ + 2². Два в кубе – это 8, а два в квадрате – это 4. Тогда 8 + 4 = 12.

Третье число 4. Подставим его в выражение. 4³ = 64. 4² = 16. Имеем 64 + 16. Получаем 80.

Следующее число 10. 10³ = 1000. 10² = 100. 1000 + 100 = 1100.

Перейдём к следующему числу. 6³ = 216. 6² = 36. 216 + 36 = 252.

Следующее число 5. Подставим его в выражение. Посчитаем. Получим 150.

Перейдём к следующему числу. Подставим его в выражение. Посчитаем. Получим 36.

И последнее число 1. Подставим его в наше выражение. Мы знаем, что единица в любой степени равна единице. Тогда получаем 1 + 1 = 2.