Представим себе такую историю…
– И как же мне это всё посчитать? – задумался Саша.
– Что случилось? – спросил у друга Паша.
– Родители предложили сделать ремонт в моей комнате, – сказал Саша.
– Да это же здорово! – порадовался за друга Паша. – Ремонт – это очень увлекательное и творческое дело.
– Конечно, ремонт – это здорово! – согласился Саша. – Но проблема в том, что родители сказали, что я должен посчитать площади стен, потолка и пола. А я не знаю, как это сделать.
– Ну, это не проблема, – сказал Паша. – Какой формы стены, потолок и пол в твоей комнате?
– Прямоугольной, – ответил Саша. – У меня, кстати, есть схема моей комнаты с размерами.
– Так показывай скорее, – предложил Паша.

– Так, так, – начал рассуждать Паша, – начнём с потолка. Он имеет форму прямоугольника размерами 5 на 4 метра. Точно такую же форму и размеры имеет пол. Что касается стен, то у нас две равные стены прямоугольной формы с размерами 5 на 3 метра и две равные стены прямоугольной формы с размерами 3 на 4 метра.
– Хорошо! – сказал Саша. – С размерами мы разобрались. А дальше как? Как нам это поможет?
– Нам понадобятся знания о площади, – сказал Паша. – Но что-то я немного запутался. У тебя ведь на одной стене есть окно квадратной формы и дверь прямоугольной формы. Их же не нужно оклеивать обоями. Давай обратимся к Электроше. Он точно сможет нам помочь.

– Ребята, прежде чем я вам расскажу о площади, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь вернёмся к вашему вопросу, – продолжил Электроша. – С такой величиной, как площадь, мы часто встречаемся в повседневной жизни. Для того чтобы положить новую плитку в вашей квартире, вам нужно приобрести определённое её количество, которое будет зависеть от площади вашей комнаты. Размер земельного участка также характеризуется площадью.

– Так что же мы понимаем под словом «площадь»?
– Площадь – это та часть плоскости, которая находится внутри фигуры, – предположили ребята.
– Правильно! – похвалил ребят Электроша. – Если говорить в общем, то площадь – это геометрическая величина, с помощью которой можно определить размер какой-либо поверхности геометрической фигуры. Кстати, измерение площадей считают одним из самых древних разделов геометрии. Даже само слово «геометрия» (в переводе с греческого – ‘землемерие’) связывают именно с измерением площадей.
– А как вы думаете, что нужно знать для того, чтобы измерить площадь фигуры? – спросил у ребят Элетроша.
– Наверное, нужно знать единицу измерения площади, – предположили мальчишки.
– Правильно! – похвалил ребят Электроша. – Напомню, что для измерения отрезков мы вводили единичный отрезок, а для измерения углов – единичный угол.

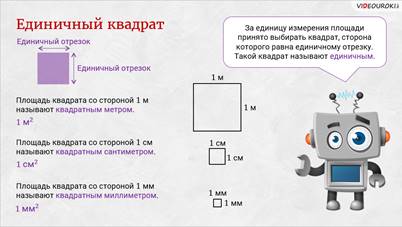
А вот за единицу измерения площади принято выбирать квадрат, сторона которого равна единичному отрезку. Такой квадрат называют единичным.
Площадь квадрата со стороной 1 метр называют квадратным
метром. Пишут так:  .
.
Площадь квадрата со стороной 1 сантиметр
называют квадратным сантиметром. Пишут так: 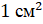 .
.
Площадь квадрата со стороной 1 миллиметр
называют квадратным миллиметром. Пишут так:  .
.
– Как вы думаете, что значит измерить площадь фигуры? – спросил у ребят Электроша.
– Измерить площадь фигуры – значит подсчитать, сколько единичных квадратов в ней помещается, – сказали мальчишки.
– Молодцы! – похвалил ребят Электроша. – Проще всего измерить площадь прямоугольника. Посмотрите: на листке бумаги изображён прямоугольник. Он состоит из четырёх полос, каждая из которых разбита на 5 квадратов со стороной 1 сантиметр. Не трудно посчитать, что весь прямоугольник состоит из 20 единичных квадратов. Обратите внимание: мы 4 умножили на 5 и получили 20. То есть площадь нашего прямоугольника равна 4 сантиметра умножить на 5 сантиметров и равна 20 квадратным сантиметрам.

Запомните! Площадь прямоугольника равна произведению
длин его соседних сторон. В буквенном виде формулу площади прямоугольника
записывают так:  , где
, где  – площадь,
– площадь,  и
и  – длины соседних сторон прямоугольника.
Важно понимать, что длина и ширина прямоугольника должны быть выражены в одних
и тех же единицах измерения.
– длины соседних сторон прямоугольника.
Важно понимать, что длина и ширина прямоугольника должны быть выражены в одних
и тех же единицах измерения.

– А теперь посмотрите на следующий рисунок, – сказал Электроша. – Что за фигура на нём изображена?
– Это квадрат со стороной 5 сантиметров, – сказал Паша.
– Хорошо! Давайте вычислим его площадь.
– Квадрат – это тоже прямоугольник, только у него все стороны равны, – начал рассуждать Саша. Воспользуемся формулой площади прямоугольника. 5 умножим на 5 и получим, что площадь нашего квадрата 25 квадратных сантиметров.

– Молодец! – похвалил Сашу Электроша. – Поскольку у квадрата все стороны равны, то его
площадь вычисляют по формуле:  , где
, где  – площадь, а – длина стороны
квадрата. Кстати, именно поэтому вторую степень числа называют квадратом числа.
– площадь, а – длина стороны
квадрата. Кстати, именно поэтому вторую степень числа называют квадратом числа.

– А теперь посмотрите на следующие три фигуры. Что вы можете сказать о них? – спросил у ребят Электроша.
– Первые две фигуры равны, так как они совпадают при наложении, – ответили мальчишки. А вот третья фигура отличается от них, то есть не равна ни первой, ни второй фигурам. Правда, она состоит из того же количества единичных квадратов.

– Вы верно заметили, – подтвердил Электроша. – Про такие фигуры говорят, что их площади равны. Запомните! Равные фигуры имеют равные площади. Однако если площади фигур равны, то не обязательно будут равными сами фигуры.

– Посмотрите на листке изображена фигура. Давайте попробуем найти её площадь.
– Какая-то неправильная фигура здесь нарисована, – задумались мальчишки.
– Данная фигура состоит из прямоугольника и
двух квадратов. Площадь прямоугольника равна  (см2). В свою очередь площадь каждого квадрата
равна 1 квадратному сантиметру. А тогда площадь всей фигуры равна 6 + 1 + 1. И
равна 8 квадратным сантиметрам.
(см2). В свою очередь площадь каждого квадрата
равна 1 квадратному сантиметру. А тогда площадь всей фигуры равна 6 + 1 + 1. И
равна 8 квадратным сантиметрам.

Запомните! Площадь фигуры равна сумме площадей фигур, из которых она состоит.

– А теперь вернёмся к единицам измерения площадей. Как мы уже говорили, площадь измеряется в квадратных единицах. Они будут различными в зависимости от размера измеряемой площади. Так, квадратным метром удобно пользоваться при расчёте площадей стен, потолка или пола. Кстати, квадратный метр принят за международную единицу измерения площадей.
Если речь идёт о маленьких предметах, то вводят квадратные дециметры, квадратные сантиметры или квадратные миллиметры. Последние нужны, если фигура не больше ногтя.
При измерении площади города или страны самыми подходящими оказываются квадратные километры. Но есть ещё и другие единицы для измерения площадей. Так, например, для измерения площади земельных участков используют ар и гектар.
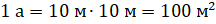 .
.
 .
.
В быту ар называют соткой.
– Ну а теперь, ребята, давайте посмотрим, как вы всё поняли, и посчитаем площади стен, потолка и пола Сашиной комнаты.
– Начнём с потолка, – предложили ребята. – Потолок является прямоугольником со сторонами 5 и 4 метра. Его площадь будет равна 20 квадратным метрам. Пол имеет такую же форму и размеры. Значит, его площадь тоже равна 20 квадратным метрам.

– Молодцы! – похвалил ребят Электроша. – Перейдём к стенам.
– У нас две стены прямоугольной формы с размерами 3 на 4 метра. Площадь каждой стены будет равна 12 квадратным метрам. Ещё у нас есть две стены прямоугольной формы с размерами 5 на 3 метра. Тогда их площадь будет равна 15 квадратным метрам.

– Всё правильно! – сказал Электроша. – Но на одной из этих стен расположены окно и дверь. Их оклеивать не нужно. Значит, мы должны из площади этой стены вычесть площадь окна и площадь двери.
– Окно квадратной формы с размерами 2 на 2 метра. Его площадь будет равна 4 квадратным метрам. Дверь прямоугольной формы с размерами 1 на 2 метра. Значит, её площадь равна 2 квадратным метрам. Осталось вычесть эти площади из площади стены. Получаем, что под поклейку обоями остаётся площадь девять квадратных метров.


 Получите свидетельство
Получите свидетельство Вход
Вход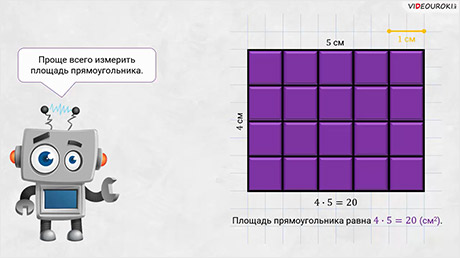



 0
0 3049
3049