Тема урока «Прямоугольный параллелепипед. Пирамида»
Представим себе такую историю…
– Да разве бывают такие длиннющие слова? – возмущался Саша.
– Что случилось? – поинтересовался Паша.
– Нам задали разгадать математический кроссворд, – сказал Саша. — А я застрял на одном слове.
– Что за слово ты не можешь разгадать? – решил уточнить Паша.
– Представляешь, это какое-то геометрическое тело, название которого состоит из четырнадцати 14 букв, – продолжал возмущаться Саша. — А ещё в этом слове есть три буквы ЭЛ и три буквы ПЭ. Да разве бывают такие слова?

– Мне кажется, я догадался! – сказал Паша. — Попробуй записать в кроссворд слово «параллелепипед».
– Как ты сказал? – решил переспросить Саша. – Па-ла-лле-ле…, па-ра-ре-ре…, па-ла-ре-ле… Да что за мудрёное слово-то такое? Язык поломаешь, пока выговоришь!
– И совсем это слово не мудрёное, – улыбнулся Паша, – а интересное. С предметами, имеющими форму параллелепипеда, ты встречаешься каждый день.
– Не встречал я такие предметы, – сказал Саша. — А если бы встречал, то уж точно бы знал это слово.
– Встречал, встречал – продолжил Паша. — Форму прямоугольного параллелепипеда можно разглядеть в зданиях на улице. Чемодан, шкаф, комод, коробка конфет, спичечный коробок, упаковочная коробка, пакет сока, микроволновка, холодильник, системный блок компьютера тоже имеют форму параллелепипеда. И даже сейчас мы с тобой находимся внутри параллелепипеда. Ведь комната – это тоже пример прямоугольного параллелепипеда.

– Но в кроссворде же было написано, что это название геометрического тела, – перебил Саша, – а ты мне тут предметы всякие перечисляешь. Они же не геометрические тела.
– Если ты внимательно посмотришь на все эти предметы, – продолжил Паша, – и не будешь обращать внимания на их цвет, материал, из которого они сделаны, их назначение и разные мелочи, то заметишь, что все они похожи своей формой. Все эти предметы напоминают геометрическое тело – прямоугольный параллелепипед.
– Забавно! – задумался Саша. — Они и впрямь похожи формой. А расскажи мне про этот па-ра-лле-ле-пи-пед поподробнее.

– Ты знаешь, лучше обратиться к Электроше, – предложил Паша, – я думаю, он больше сможет рассказать.
– Ребята, прежде чем я вам расскажу о прямоугольном параллелепипеде, давайте немного разомнёмся и выполним устные задания, – предложил Электроша. (пауза)
– Давайте сверимся! Посмотрите, что у вас должно было получиться! (пауза)

– А теперь вернёмся к вашему вопросу, – продолжил Электроша. — Итак, прямоугольный параллелепипед – это такая объёмная фигура, а точнее, это геометрическое тело, которое состоит из шести 6 прямоугольников.
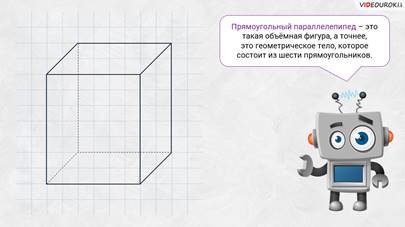
– Электроша, ты сказал «прямоугольный» параллелепипед, – решил уточнить Саша. – А что, бывают ещё и другие параллелепипеды?
– Да, бывают и непрямоугольные параллелепипеды, – ответил Электроша, – но мы с ними познакомимся в старших классах. А сейчас мы поговорим о прямоугольном параллелепипеде.

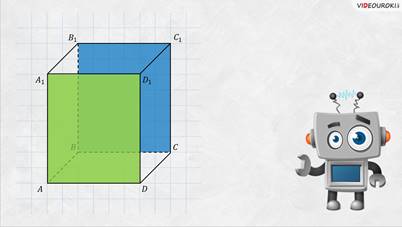
– Посмотрите на экран. На рисунках изображены два прямоугольных параллелепипеда. Правда, на первом рисунке представлена модель прямоугольного параллелепипеда, а на втором – его математическое представление – изображение.
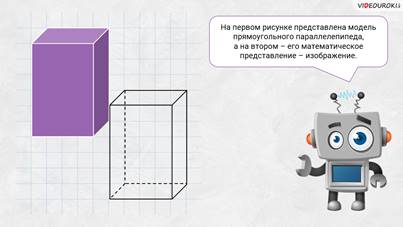
– Электроша, а у прямоугольного параллелепипеда тоже есть свои элементы, как и у других геометрических фигур? – спросил Паша.
–
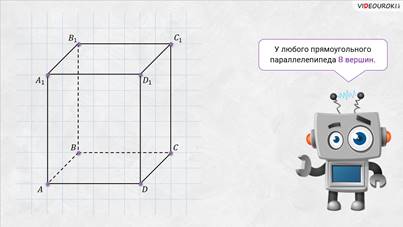
Конечно! – сказал Электроша. — Давайте рассмотрим прямоугольный параллелепипед 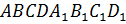 А Бэ Цэ Дэ А
один Бэ один Цэ один Дэ один.
А Бэ Цэ Дэ А
один Бэ один Цэ один Дэ один.
У
любого прямоугольного параллелепипеда восемь 8 вершин.
Так, у нашего прямоугольного параллелепипеда вершинами являются точки 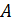 А,
А,
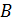 Бэ,
Бэ,
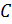 Цэ,
Цэ,
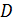 Дэ,
Дэ,
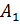 А один,
А один,
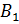 Бэ один,
Бэ один,
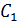 Цэ один
и
Цэ один
и 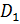 Дэ один.
Дэ один.
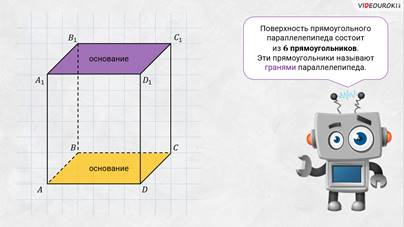
Поверхность
прямоугольного параллелепипеда состоит из шести 6 прямоугольников.
Эти прямоугольники называют гранями параллелепипеда. Так, у
нашего параллелепипеда есть верхняя грань 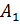 А один
А один 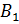 Бэ один
Бэ один 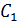 Цэ один
Цэ один 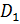 Дэ один,
нижняя грань
Дэ один,
нижняя грань  А Бэ Цэ Дэ.
Эти грани ещё называют основаниями
прямоугольного параллелепипеда.
А Бэ Цэ Дэ.
Эти грани ещё называют основаниями
прямоугольного параллелепипеда.
Дальше
– передняя грань 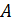 А
А 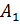 А один
А один 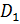 Дэ один
Дэ один 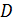 Дэ,
задняя грань
Дэ,
задняя грань 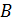 Бэ
Бэ 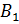 Бэ один
Бэ один 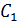 Цэ один
Цэ один 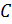 .Цэ
.Цэ
и И две
боковые грани 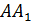 А А один
А А один 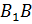 Бэ один Бэ
и
Бэ один Бэ
и 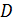 Дэ
Дэ 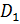 Дэ один
Дэ один 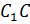 Цэ один Цэ.
Цэ один Цэ.
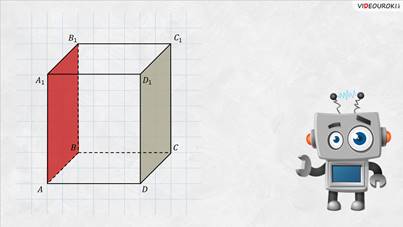
Обратите внимание: грани, расположенные напротив друг друга, не имеют общих вершин. Такие грани называют противолежащими, или вы можете ещё услышать противоположными. Запомните! Противолежащие грани прямоугольного параллелепипеда равны.
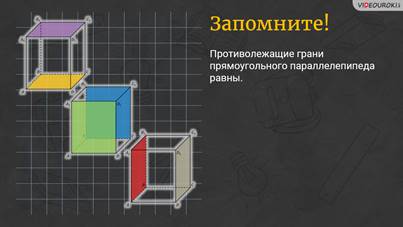
– То есть в нашем параллелепипеде три 3 пары равных граней? – решил уточнить Саша.
–
Правильно! У прямоугольного параллелепипеда три 3 пары
равных граней, – ответил Электроша. — Продолжим дальше рассматривать наш
параллелепипед. Стороны граней называют рёбрами прямоугольного
параллелепипеда. Всего прямоугольный параллелепипед имеет двенадцать 12 рёбер.
Обратите внимание: рёбра 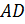 А Дэ,
А Дэ,
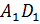 А один Дэ один,
А один Дэ один,
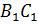 Бэ один Цэ
один и
Бэ один Цэ
один и 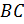 Бэ Цэ
равны. Рёбра
Бэ Цэ
равны. Рёбра 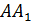 А А один,
А А один,
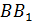 Бэ Бэ один,
Бэ Бэ один,
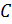 Цэ
Цэ 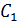 Цэ один
и
Цэ один
и 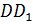 Дэ Дэ один
тоже равны. Также равны и рёбра
Дэ Дэ один
тоже равны. Также равны и рёбра 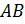 А Бэ,
А Бэ,
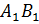 А один Бэ один,
А один Бэ один,
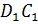 Дэ один Цэ
один и
Дэ один Цэ
один и 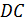 Дэ Цэ.
Дэ Цэ.
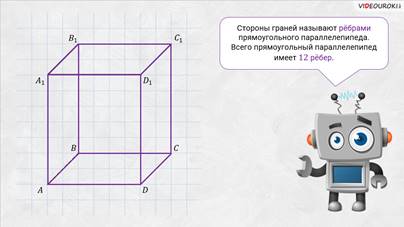
– Электроша, получается, что у прямоугольного параллелепипеда восемь 8 вершин, шесть 6 граней и двенадцать 12 рёбер? – решил уточнить Паша.
– Именно так, – подтвердил Электроша. — Это и есть основные элементы прямоугольного параллелепипеда.
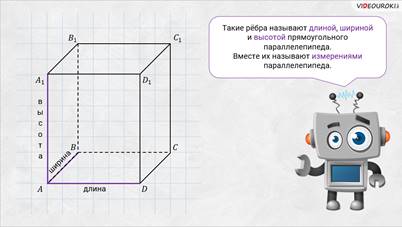
Посмотрите: в каждой вершине прямоугольного параллелепипеда сходятся три ребра. Такие рёбра называют длиной, шириной и высотой прямоугольного параллелепипеда. Вместе их называют измерениями параллелепипеда.
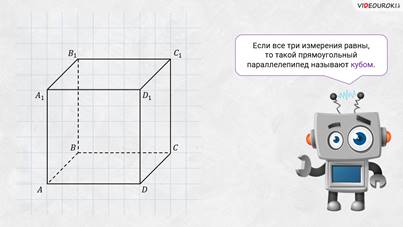
– Если все три измерения равны, то такой прямоугольный параллелепипед называют кубом, – продолжил Электроша. Нетрудно догадаться, что поверхность куба состоит из шести 6 равных квадратов. Кроме того, все двенадцать 12 рёбер куба также равны.
– Тела имеют разные свойства. Одним из свойств является масса, которую находят с помощью весов. А вот другим свойством тел является площадь поверхности.
– Это как площадь в прямоугольнике? – спросил Саша.
–
Да, – ответил Электроша, – отличие лишь в том, что прямоугольный параллелепипед
– это объёмная фигура, а так как прямоугольный параллелепипед имеет шесть 6 граней
– прямоугольников, причём противолежащие грани его попарно равны, то площадь
поверхности прямоугольного параллелепипеда будет равна сумме площадей его шести 6 граней,
при этом площади противолежащих граней будут равны. Запомните! Площадью
поверхности параллелепипеда называют сумму площадей всех его граней. Если
измерения нашего прямоугольного параллелепипеда обозначить таким образом: a
– его длина, бэ b –
ширина и цэ c –
высота, то площадь его поверхности можно вычислить следующим образом: 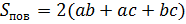 ….
….

Если
прямоугольный параллелепипед является кубом с длиной ребра равной а, то площадь
его поверхность можно записать так: 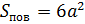 ….
….

– А теперь давайте проведём небольшой эксперимент – предложил Электроша. — Возьмём коробку, имеющую форму прямоугольного параллелепипеда.
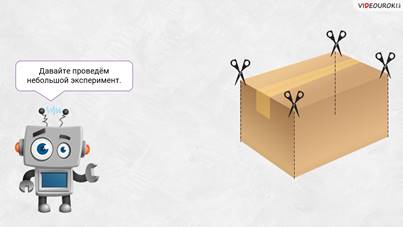
Откроем её, затем разрежем по четырём вертикальным рёбрам, а потом развернём.

– И что за странную фигуру мы получили? – спросил Саша.
– Фигуру, которая у нас получилась, называют развёрткой прямоугольного параллелепипеда. С помощью развёртки можно изготовить модель прямоугольного параллелепипеда.
Как вы думаете, вот такая развёртка какому геометрическому телу принадлежит?

– Да это же развёртка куба! – догадался Паша. — Она состоит из шести 6 равных квадратов.
– Молодец! – похвалил Пашу Электроша. — А теперь посмотрите на следующую картинку. Что вы видите на ней?

– Да это же одно из семи чудес света – египетские пирамиды, – воскликнули ребята, — нам про них рассказывали на уроках истории.
– Молодцы! – похвалил ребят Электроша. — Среди множества разнообразных геометрических тел есть большая группа, которая называется многогранниками.

Многогранники – это геометрические тела, поверхность которых состоит из многоугольников. Параллелепипед и пирамида являются видами многогранников.
– Электроша, а расскажи нам про пирамиды, – попросили робота мальчишки.
– С радостью, – улыбнулся Электроша. — Посмотрите на рисунок. На нём изображена пирамида.
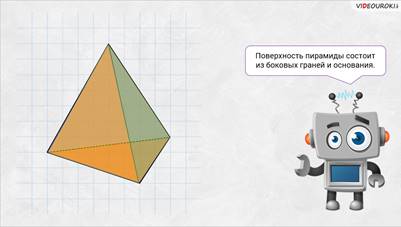
Нетрудно заметить, что поверхность нашей пирамиды состоит из боковых граней и основания. Причём боковые грани пирамиды всегда являются треугольниками, имеющими общую вершину. Эту общую вершину боковых граней называют вершиной пирамиды. А стороны граней называют рёбрами пирамиды.
– Электроша, ты сказал, что пирамида состоит из боковых граней и основания и что все боковые грани — всегда треугольники. А что, в основании пирамиды может лежать не треугольник? – спросил Паша.
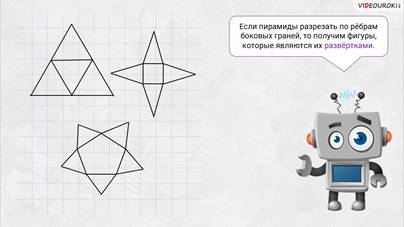
– Хороший вопрос! – обрадовался Электроша. — В основании пирамиды может лежать любой многоугольник. И в зависимости от того, какой многоугольник лежит в основании, все пирамиды можно разделить на треугольные, четырёхугольные, пятиугольные и так далее. Перед вами примеры таких пирамид.
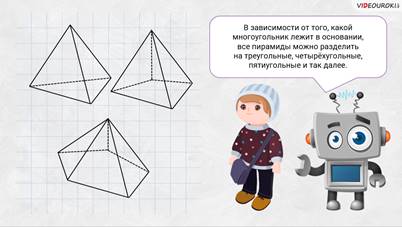
– Если пирамиды разрезать по рёбрам боковых граней, то получим фигуры, которые являются их развёртками.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
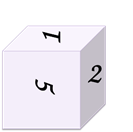
Задание первое: есть четыре изображения одного кубика с разных сторон.
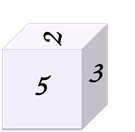
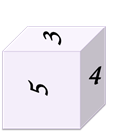
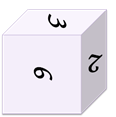
Восстановите развёртку данного кубика по известной её части.
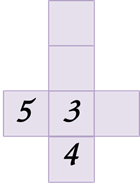
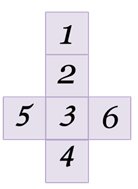
Решение: из первого изображения видно, что единичка 1 расположена над двойкой2. Рассматривая второе изображение кубика, можно сделать вывод, что тройка 3 расположена под двойкой2. Из следующего изображения делаем вывод, что четвёрка 4 расположена под тройкой3. А из последнего изображения можем заметить, что шестёрка 6 расположена справа от тройки3. Сопоставляя все сделанные выводы и часть развёртки, которая известна, получим следующую развёртку кубика…:
Следующее задание: Миша хочет покрасить деревянный брусок в форме прямоугольного параллелепипеда. Сколько потребуется краски, если измерения этого бруска два 2 сантиметра, три 3 сантиметра, четыре 4 сантиметра и известно, что для покраски одного квадратного сантиметра поверхности потребуется два 5 грамма краски?

Решение: прежде
чем узнать, сколько понадобится краски, нужно вычислить площадь поверхности
бруска. Так как брусок имеет форму прямоугольного параллелепипеда, то можем
воспользоваться формулой площади поверхности прямоугольного параллелепипеда: 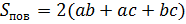 ….
Подставим измерения нашего бруска в формулу. Получим:
….
Подставим измерения нашего бруска в формулу. Получим: 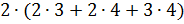 два умножить
на сумму произведений двух и трёх, двух и четырёх, трёх и четырёх.
Посчитаем и получим, что площадь поверхности нашего бруска равна пятидесяти
двум52 квадратным сантиметрам.
два умножить
на сумму произведений двух и трёх, двух и четырёх, трёх и четырёх.
Посчитаем и получим, что площадь поверхности нашего бруска равна пятидесяти
двум52 квадратным сантиметрам.
Из
условия задачи мы знаем, что на один 1 квадратный
сантиметр поверхности потребуется два 2 грамма краски.
Значит, 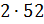 два умножим на
пятьдесят два. Получим сто четыре104 грамма.
два умножим на
пятьдесят два. Получим сто четыре104 грамма.
Ответ: сто четыре104 грамма краски потребуется для покраски бруска.

– Паша, Саша, молодцы! – воскликнул Электроша. — Ну и давайте напоследок повторим, что нового вы сегодня узнали.
Многогранники – это геометрические тела, поверхность которых состоит из многоугольников.
Параллелепипед и пирамида являются видами многогранников.
Прямоугольный параллелепипед – это многогранник, поверхность которого состоит из шести прямоугольников.
У прямоугольного параллелепипеда восемь вершин, шесть граней и двенадцать рёбер.
Грани прямоугольного параллелепипеда, расположенные напротив друг друга и не имеющие общих вершин, называют противолежащими.
Противолежащие грани прямоугольного параллелепипеда равны.
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, называют измерениями (длиной, шириной и высотой).
Если все три измерения равны, то такой прямоугольный параллелепипед называют кубом.
Площадью поверхности параллелепипеда называют сумму площадей всех его граней.
Пирамида – это многогранник, у которого все боковые грани — треугольники.
В зависимости от того, какой многоугольник лежит в основании, все пирамиды можно разделить на треугольные, четырёхугольные, пятиугольные и так далее.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 6329
6329

