Представим себе такую историю…
– Паша, а ты когда-нибудь собирал кубик Рубика? – спросил Саша.
– Конечно! И не один раз, – ответил Паша. – Кстати, кубик Рубика отличная игрушка-головоломка, которая развивает логическое мышление.
– Да, мне тоже он очень нравится! – продолжил Саша. – Я вот сегодня собрал кубик Рубика за 15 минут. Пока собирал, задумался, а сколько всего маленьких кубиков в нём?
– И в правду, – задумался Паша, – и сколько же их там?
– Не знаю! – ответил Саша. – Сколько ни пытался их пересчитать, всё сбивался. В общем, так и не получилось у меня их сосчитать.

– А давай спросим у Электроши! – предложил Паша. – Он точно знает, как их посчитать.
– Ребята, прежде чем я вам расскажу о прямоугольном параллелепипеде, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
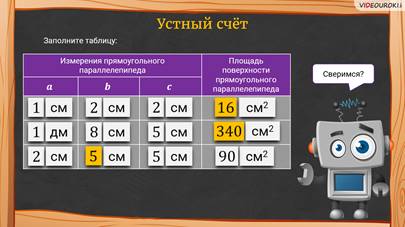
– А теперь вернёмся к вашему вопросу, – продолжил Электроша. – Только сначала ответьте мне на вопрос: какую форму имеет кубик Рубика?
– Кубик Рубика имеет форму прямоугольного параллелепипеда, а точнее – форму куба, – ответили мальчишки.
– Молодцы! – похвалил ребят Электроша. – Важным свойством любого геометрического тела является его вместимость, то есть объём фигуры. Величина объёма даёт нам представление о том, какую часть пространства занимает интересующий нас объект.

Кстати, с такой величиной, как объём, мы очень часто встречаемся в нашей жизни. Может, вы сможете привести примеры, когда мы интересуемся объёмом? – спросил у ребят Электроша.
– Например, объём коробки с соком, объём бассейна, объём школьного кабинета, – начал Саша.
– Ещё нам нужно знать объём топливного бака машины, показатели потребления газа или воды на счётчиках, – продолжил Паша.

– Хорошие примеры! – похвалил ребят Электроша. – А как вы думаете, что нужно знать для того, чтобы измерить объём? – спросил у ребят Электроша.
– Наверное, нужно знать единицу измерения объёмов, – предположили мальчишки.
– Правильно! – подтвердил Электроша. – Напомню, что для измерения отрезков мы вводили единичный отрезок, для измерения углов – единичный угол, а для измерения площадей фигур – единичный квадрат.
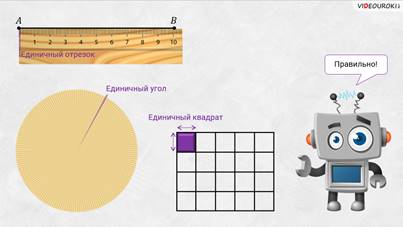
Для измерения объёмов также вводятся единицы измерения. За единицу измерения объёма выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Например, объём куба с ребром 1 миллиметр
называют кубическим миллиметром. Пишут так: 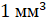 .
.
Объём куба с ребром 1 сантиметр называют кубическим
сантиметром. Пишут так: 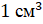 .
.
Объём куба с ребром 1 дециметр называют кубическим
дециметром. Пишут так: 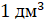 .
.

Всем хорошо известна и такая единица объёма,
как 1 литр. Пишут так 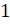 дм3
дм3 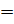
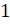 л. Это другое название кубического
дециметра.
л. Это другое название кубического
дециметра.

Объём куба с ребром 1 метр называют кубическим
метром. Пишут так: 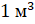 .
.
Объём куба с ребром 1 километр называют кубическим
километром. Пишут так: 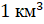 .
.

Легко заметить, что название единицы объёма получается из названия единицы длины присоединением прилагательного «кубический».
– Как вы думаете, что значит измерить объём фигуры? – спросил у ребят Электроша.
– Измерить объём фигуры – значит подсчитать, сколько единичных кубов в ней помещается, – сказали мальчишки.
– Молодцы! – похвалил ребят Электроша. – Проще всего измерить объём прямоугольного параллелепипеда. Чем мы сейчас и займёмся.
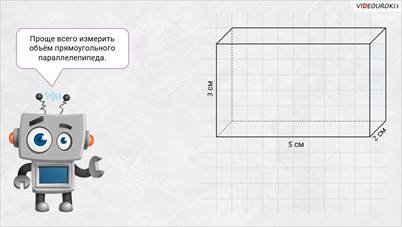
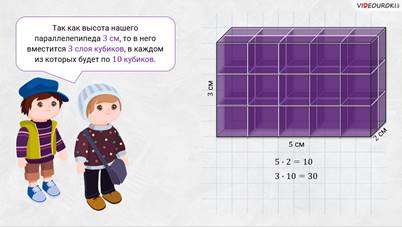
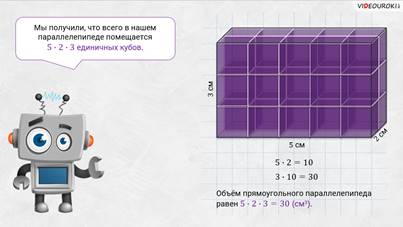
– Посмотрите: на листке бумаги изображён прямоугольный параллелепипед со следующими измерениями: длина 5 сантиметров, ширина 2 сантиметра и высота 3 сантиметра. Давайте посчитаем, сколько единичных кубов может в нём поместиться.
– Начнём укладывать кубики на дно прямоугольного параллелепипеда, – предложили мальчишки. – Итак, сначала положим на дно ряд единичных кубиков со стороной 1 сантиметр вдоль длинной стены. Видим: поместилось 5 таких кубиков. Затем вдоль этих кубиков уложим ещё 1 ряд. Тоже получим ещё пять кубиков.
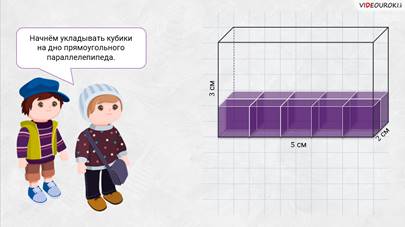
– Хорошо! – сказал Электроша. – Тогда сколько всего кубиков у вас поместилось на дне прямоугольного параллелепипеда?
– На дне параллелепипеда помещается слой из 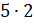 единичных кубиков, то есть слой из 10 кубов.
единичных кубиков, то есть слой из 10 кубов.
– Молодцы! – похвалил ребят Электроша. – А чтобы заполнить весь прямоугольный параллелепипед, сколько в него нужно вложить таких слоёв?
– Так как высота нашего параллелепипеда 3 сантиметра, то в него вместится 3 слоя кубиков, в каждом из которых будет по 10 кубиков. Тогда получается, что весь прямоугольный параллелепипед можно заполнить 30 кубиками.
– Всё правильно! – согласился Электроша. – Мы получили, что всего в нашем параллелепипеде
помещается 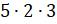 единичных кубов. Поэтому объём нашего параллелепипеда равен
единичных кубов. Поэтому объём нашего параллелепипеда равен 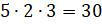 (см3).
(см3).
– Электроша, получается, что три измерения прямоугольного параллелепипеда позволяют посчитать, сколько всего кубиков в нём поместится? – спросил Паша.
– Да, – ответил Электроша. – Запомните! Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Формулу для вычисления объёма прямоугольного
параллелепипеда в буквенном виде можно записать следующим образом: 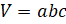 , где
, где 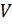 – объём,
– объём, 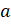 ,
, 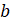 и
и 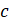 – измерения прямоугольного параллелепипеда.
При вычислениях обязательно нужно обращать внимание, чтобы все измерения
прямоугольного параллелепипеда были выражены в одинаковых единицах.
– измерения прямоугольного параллелепипеда.
При вычислениях обязательно нужно обращать внимание, чтобы все измерения
прямоугольного параллелепипеда были выражены в одинаковых единицах.

– А теперь давайте решим одну задачку, – предложил Электроша. – Определите объём блока бумаги, если длина одного листа 20 миллиметров, ширина – 15 миллиметров, а всего в блоке помещается 500 таких листов (считать толщину листа равной 1 миллиметру).
– Сначала вычислим площадь одного листа, –
сказал Паша, – она будет равна 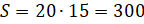 (мм2).
(мм2).
– А потом площадь этого листа умножим на
количество листов, помещающихся в блоке, – продолжил Саша, – то есть 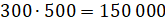 (мм3).
(мм3).

– Молодцы! – похвалил ребят Электроша. – Обратите внимание: блок бумаги имеет форму прямоугольного параллелепипеда. Значит, мы с вами сейчас нашли объём параллелепипеда, но с помощью другой формулы. Запомните! Объём прямоугольного параллелепипеда равен произведению площади основания на высоту.
В буквенном виде эту формулу записывают так: 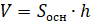 , где
, где 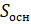 – площадь основания прямоугольного
параллелепипеда,
– площадь основания прямоугольного
параллелепипеда, 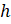 – его высота.
– его высота.

– А теперь давайте всё же вернёмся к вашему первоначальному вопросу, – продолжил Электроша. – Вы хотели выяснить, сколько кубиков содержится в кубике Рубика. Мы с вами уже определили, что эта замечательная игрушка имеет форму прямоугольного параллелепипеда, а если быть точнее, то форму куба. Может, вы уже сможете посчитать количество маленьких кубиков, из которых состоит кубик Рубика?
– Так, – начал рассуждать Саша, – длина
нашего кубика Рубика состоит из 3 маленьких кубиков, точно
такие же ширина и высота. Значит, в нашем кубике Рубика
помещается 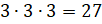 маленьких кубиков.
маленьких кубиков.

– Всё правильно! – сказал Электроша. – Изначально кубик Рубика состоял из 27 связных между собой разноцветных кубиков, но затем его конструкция упростилась до набора из 26 маленьких кубиков, а вместо внутреннего кубика разместился хитроумный скрепляющий механизм. Кстати, а вы знаете кем, как и когда была придумана эта замечательная игрушка? – спросил Электроша.
– Не знаем, – ответили мальчишки.
– Скажу вам только, что знаменитый кубик Рубика придумал венгерский преподаватель архитектуры Эрно Рубик в 1974 году.

А вот уже историю его создания и усовершенствования вы можете изучить на досуге.
– А теперь смотрите, мы с вами определили,
что наш кубик Рубика имеет форму куба. Поскольку у
куба все рёбра равны, то его объём вычисляют по формуле: 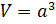 , где
, где 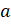 – длина ребра куба. Именно поэтому третью
степень числа называют кубом числа.
– длина ребра куба. Именно поэтому третью
степень числа называют кубом числа.

А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: объём класса 96 кубических метров. Найдите высоту стены, если площадь пола 32 квадратных метра.

Решение: класс имеет форму прямоугольного
параллелепипеда. Нам известна площадь пола, то есть площадь основания
прямоугольного параллелепипеда. Значит, можем воспользоваться формулой для
вычисления объёма прямоугольного параллелепипеда через площадь основания и
высоту: 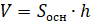 . Выразим из этой формулы высоту:
. Выразим из этой формулы высоту: 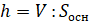 . И подставим в получившуюся формулу объём класса и площадь пола:
. И подставим в получившуюся формулу объём класса и площадь пола: 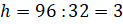 (м). Получаем, что высота стены равна 3 метрам.
(м). Получаем, что высота стены равна 3 метрам.

Следующее задание: длина аквариума 80 сантиметров, ширина 45 сантиметров, высота 65 сантиметров. Сколько литров воды нужно налить, чтобы уровень воды был ниже верхнего края аквариума на 5 сантиметров?

Решение: высота нашего аквариума 65
сантиметров, а воду нужно налить так, чтобы её уровень был ниже верхнего края
аквариума на 5 сантиметров. Значит, от высоты аквариума отнимем 5 сантиметров:  . Получим, что высота уровня воды равна 60 сантиметрам. Воспользуемся
формулой для вычисления объёма прямоугольного параллелепипеда:
. Получим, что высота уровня воды равна 60 сантиметрам. Воспользуемся
формулой для вычисления объёма прямоугольного параллелепипеда:
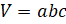 . Получим, что в аквариум нужно налить
. Получим, что в аквариум нужно налить 
 (см3). Переведём в литры. Мы знаем, что
(см3). Переведём в литры. Мы знаем, что  л
л  дм3 , а значит, равен
дм3 , а значит, равен  см3 . Тогда получаем, что в
аквариум нужно налить
см3 . Тогда получаем, что в
аквариум нужно налить  см3
см3  л.
л.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 3599
3599

