– Сок и кекс или молоко и булочка? – размышлял Саша, идя по улице.
Паша спросил у Саши: А, что ты такое бормочешь? Что это за сок и кекс или молоко и булочка?
– Паша, понимаешь, – сказал Саша, – мама сказала, что на полдник я могу выбирать сок, компот или молоко и кекс, булочку или яблочный пирог. Вот я иду и решаю, что же я хочу съесть. Вариантов выбора очень много.

– Да, Саша, ты прав, – согласился с другом Паша, – выбирать всегда трудно. А вот интересно, сколько всего вариантов может получиться? Может, их будет сто тысяч миллионов?

И Саша предложил Паше вместе с ним подсчитать все варианты возможного полдника.
– Я могу выбрать сок и булочку – это один вариант. Могу выбрать сок и кекс – это второй вариант. А могу компот и булочку – начал перечислять варианты Саша.
Ещё ты можешь выбрать молоко и булочку.

– Да, – сказал Саша, – так мы будем перебирать до вечера. Вот бы узнать, сколько всего вариантов полдника у меня получится.
Паша предложил пойти к их другу – роботу Электроше.
– Электроша, привет. У нас для тебя новый вопрос. Смотри, Саше на полдник предложили на выбор напиток: молоко, компот и сок, а к напитку, тоже на выбор, предложили кекс, булочку и яблочный пирог. Как нам подсчитать все возможные варианты? И можно ли это сделать?
– Да, мальчики, все варианты подсчитать можно, и сделать это просто, – ответил робот. Но давайте сделаем небольшую разминочку и немного порешаем устно.

– Вернёмся к вашей задаче, – продолжил Робот. На самом деле, таких задач, в которых нужно сделать выбор, очень много. Просыпаясь, мы выбираем что одеть, чем позавтракать. Собираясь куда-то ехать, мы выбираем маршруты и так далее.

Такие задачи называют комбинаторными.
Саша переспросил: Как? Ком-би-на-тор-ные? А почему их назвали именно так?
– Потому что в таких задачах необходимо подсчитать все возможные случаи или, по-другому, все возможные комбинации.

– А-а-а, – протянул Паша, – теперь понятно! А как же решать такие задачи?
– Сейчас всё расскажу, – ответил Электроша. Давайте составим таблицу.
В первой строке запишем: Кекс, булочка, яблочный пирог, а в первом столбце – сок, компот и молоко.

Теперь в пустые клеточки запишем сочетания. Для удобства все названия сократим до одной буквы. Но, чтобы различить компот и кекс, компот обозначим двумя буквами Ко. В этой клеточке пересекаются сок и кекс, поэтому запишем здесь СК. В эту клеточку нам что надо записать, Саша? – спросил робот у мальчика.
Мальчик начал размышлять: В этой клеточке пересекаются сок и булочка, значит, сюда надо вписать буквы С и Б.

– Молодец, Саша! – похвалил мальчика робот.
– Теперь ты, Паша, попробуй.
Паша подумал немного и сказал: В этой клеточке надо писать С и Я, потому что она стоит на пересечении сока и яблочного пирога.

– Молодцы, ребята! Вы всё верно поняли, – похвалил детей робот. – Теперь для вас не составит труда заполнить всю таблицу и подсчитать, сколько вариантов полдника получится.

Мальчики вместе заполнили таблицу и ответили на свой вопрос: Ого! – воскликнул Паша, – смотри, Саша, тебе надо выбирать из 9 вариантов.
– Да, – согласился Саша, – это не так уж и много.
Тут Электроша решил прервать мальчиков: Сейчас я вам покажу ещё один способ решения вашей задачи. С помощью дерева.
– Какого ещё дерева? – удивились ребята. Берёзы, липы или клёна?
– Нет, – успокоил Сашу и Пашу робот, – для решения комбинаторных задач очень удобно использовать специальное дерево возможных вариантов. Это схема, на которой все варианты чётко видны. Сейчас сами всё увидите.
Итак. Мы с вами выбираем варианты полдника, поэтому сверху напишем «Полдник».
У нас 3 варианта выбора напитка. От полдника опустим 3 линии и подпишем их соответственно: С (сок), Ко (компот) и М (молоко). Для каждого из напитков можно выбрать один из 3 десертов, значит, от каждой буквы опускаем по 3 линии и подписываем: К (кекс), Б (булочка) и Я (яблочный пирог). Теперь нам остаётся подсчитать, сколько «веточек» у нас получилось. Их будет 9. Значит, и вариантов полдника будет 9.

– Здорово! – восхитились мальчишки, – и мы хотим построить такие деревья. Электроша, можешь для нас придумать задачи?
И робот составил для мальчиков такое задание.
– В кружок бальных танцев записались 2 мальчика – Костя и Женя, и 3 девочки – Оля, Настя и Вика. Какие танцевальные пары девочки и мальчики могут организовать?
Паша предложил назвать дерево выбора: «Кружок бальных танцев». Но тут вмешался Электроша.
– Иногда, когда название для дерева выбора сложно подобрать или оно очень большое, сверху ставят просто звёздочку.
Теперь Саша решил внести свою лепту в решение задачи.
– В паре обязательно должен быть мальчик, мальчиков всего 2, значит, от названия надо опустить 2 линии и подписать: К (Костя) и Ж (Женя).
– Девочек у нас 3, – добавил Паша, – значит, от каждой буквы надо опустить по 3 линии и подписать О (Оля), Н (Настя) и В (Вика).
Теперь подсчитаем, сколько «веточек» у нас получилось, и увидим, что из двух мальчиков и трёх девочек можно составить 6 пар. Правильно?

– Да, – сказал Электроша, – вы справились.
Тут Паша спросил: Вот интересно, а если бы мы в дереве начинали не с мальчиков, а с девочек, у нас получился бы такой же ответ?
– Попробуйте, – предложил робот ребятам. – Решите эту задачу ещё раз.
– Итак, – начал Паша. Девочка должна быть в паре обязательно, значит, от названия опускаем 3 линии и ставим буквы О, Н, и В. Теперь от каждой буквы опускаем по 2 линии, потому что мальчиков у нас всего 2, и ставим буквы К и Ж. И опять получаем 6 пар. То есть совсем нет разницы, с чего начинать?

– Конечно, нет, – сказал робот, – дело в том, что с помощью дерева выбора мы перебираем все возможные варианты. Поэтому и нет разницы, с чего начинать.
Выполним ещё одно задание. Сколько трёхзначных чисел можно составить из цифр 0, 3 и 7?
Саша начал решать: Сверху поставим звёздочку, а то называть дерево выбора «Трёхзначное число» – это очень долго. У нас 3 числа, значит, опустим 3 линии и напишем 0, 3, 7.
– Подожди, Саша, – перебил друга Паша. – А разве трёхзначное число может начинаться с нуля? Это же тогда получится двухзначное число. Или нет? Рассуди нас, Электроша.
– Да, ты прав, Паша, – сказал робот. – Действительно, условие о том, что нам надо составить трёхзначное число, уже сразу показывает, что 0 первым стоять не может.
Чтобы вам было удобнее, давайте подпишем, какую цифру числа мы выбираем.
– Я всё понял, – сказал Саша. – От звёздочки мы должны опустить 2 линии и подписать их 3 и 7. Это будут варианты для первой цифры трёхзначного числа.
А вот теперь от каждого числа уже можно опустить 3 линии и написать 3 числа: 0, 3 и 7. Ведь эти «веточки» определяют вторую цифру трёхзначного числа, а она может быть любой, даже нулём. Третью цифру тоже можно выбрать из трёх цифр.
Теперь давайте подсчитаем общее количество чисел, которое получилось.

Оказалось, что из цифр 0, 3 и 7 можно составить 18 трёхзначных чисел.
– Вы так хорошо справляетесь с моими задачами, что я хочу показать вам, как ещё можно решать комбинаторные задачи, – сказал мальчикам Электроша.
– При встрече 4 друга обмениваются рукопожатиями. Сколько всего рукопожатий получилось? Сначала давайте попробуем решить эту задачу с помощью дерева выбора.
– Назовём это дерево «Рукопожатия». У нас 4 мальчика, значит, опускаем 4 линии. Для удобства мальчиков будем обозначать числами от 1 до 4.
Каждый должен поздороваться с каждым. То есть от каждой цифры надо опустить по 3 палочки и поставить числа.
Теперь давайте выпишем все получившиеся варианты. Посмотрите, у нас есть варианты 1 2 и 2 1. То есть первый мальчик пожимает руку второму и второй пожимает первому. Но это одно и то же рукопожатие, поэтому вычеркнем все лишние получившиеся варианты и получим, что всего будет сделано 6 рукопожатий.

Но эту задачу можно было решить проще.
– Как проще? – спросил Саша.
– Да, Саша, есть ещё один способ решения именно таких комбинаторных задач. Отметим 4 точки. Это будут друзья, про которых говорится в условии.
Рукопожатия обозначают, что каждые 2 точки должны быть соединены. Проведём отрезки через каждые 2 точки. Нам остаётся только подсчитать, сколько отрезков получится. Их 6, то есть всего было сделано 6 рукопожатий.

Ответ получился тот же, но решали мы задачу намного быстрее.

 Получите свидетельство
Получите свидетельство Вход
Вход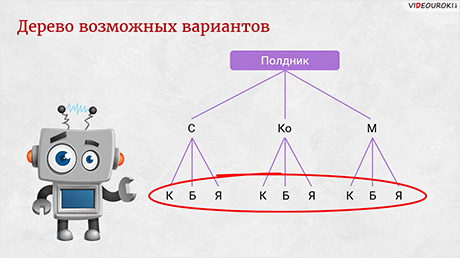



 0
0 3880
3880

