Вероятности элементарных событий. Равновозможные элементарные события

Прежде чем приступить к рассмотрению новой темы, напомним, что элементарными событиями (или элементарными исходами) называют события случайного эксперимента, которые нельзя разделить на более простые.

В каждом эксперименте можно выделить элементарные события, из которых состоят все остальные события.

В результате случайного эксперимента обязательно наступает только одно элементарное событие.

Поговорим о вероятностях элементарных событий.

Пусть 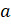,  и  – элементарные события некоторого случайного эксперимента. Обозначим вероятности событий ,  и .

Можно считать, что весь случайный эксперимент – это одно большое событие, которое обязательно наступит (оно достоверно), и приписать ему максимальную вероятность, равную 1.

В результате эксперимента какое-то одно из одно из элементарных событий обязательно наступает. Причём только одно (два элементарных события наступить не могут).

Поэтому вероятности элементарных событий нужно назначать, следуя двум правилам.

Первое правило. Вероятности элементарных событий неотрицательны.

Второе правило. Сумма вероятностей всех элементарных событий равна 1.

Тогда для элементарных событи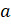й ,  и  должно выполняться равенство

.

Это свойство вероятностей является отражением такого же свойства частот: в любом наборе сумма частот значений равна 1.

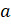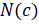Повторим рассматриваемый случайный эксперимент  раз. Пусть элементарное событие  произошло  раз, элементарное событие  произошло  раз, а элементарное событие  произошло  раз.

Тогда частоты элементарных событи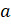й ,  и  соответственно равны , , . Сумма этих частот равна 1.

В некоторых случаях вероятности элементарных событий можно рассчитать. В других случаях их можно оценить с помощью частот, проведя множество наблюдений. А иногда вероятности элементарных событий никак не удаётся определить.

Особым является случай, когда элементарные события в эксперименте имеют одинаковые шансы. Например, при однократном бросании игрального кубика могут наступить элементарные события: выпадет 1 очко, выпадет 2 очка, выпадет 3 очка, выпадет 4 очка, выпадет 5 очков и выпадет 6 очков.

Если игральный кубик симметричный, то есть правильный, то шансы этих шести элементарных событий одинаковы.

Или, например, при однократном подбрасывании монеты могут наступить элементарные события: выпадет орёл, выпадет решка.

Если монета математическая, то есть симметричная, то шансы этих двух элементарных событий одинаковы.

Если в случайном эксперименте шансы всех элементарных событий одинаковы, то он называется случайным экспериментом с равновозможными элементарными событиями.

При двукратном подбрасывании игрального кубика может наступить одно из 36 элементарных событий, и все они равновозможны.

Опыты с равновозможными элементарными событиями возникают при бросании игральных кубиков, подбрасывании монет, в лотереях, жребиях, социологических исследованиях и других искусственных экспериментах.

Но равновозможные элементарные события возникают не только в играх или опросах.

Например, в мобильных телефонах используются алгоритмы шифрования. В этих алгоритмах применяются случайные числа – десятичные дроби, которые с равными шансами выбираются из интервала от 0 до 1. Программа для создания случайных чисел называется генератором случайных чисел.

В природе опыты с равновозможными элементарными событиями встречаются очень редко.

Предположим, что в некотором случайном эксперименте  элементарных событий. Вероятность каждого элементарного события равна .

Запишем сумму  слагаемых, каждое из которых равно , как .

Из этого равенства получим, что .

Сформулируем правило, позволяющее назначать вероятности элементарных событий.

Если в случайном эксперименте ровно  равновозможных элементарных событий, то вероятность каждого из них равна .

Эксперименты с равновозможными элементарными событиями очень важны, несмотря на то что в природе они практически не встречаются. А всё потому, что с помощью искусственных опытов с равновозможными событиями часто удаётся находить приближённые решения важных сложных задач. Также эксперименты с равновозможными событиями удобны при изучении теории вероятностей, так как теорию вероятностей начинают изучать именно с таких опытов. Но будьте осторожны, ведь не во всех экспериментах элементарные события равновозможны.

Давайте поговорим об ошибке Д'Аламбера – французского учёного, который жил в XVIII веке. Он изучал математику и физику. В 1764 году был избран почётным членом Санкт- Петербургской академии наук, хотя ни разу не был в России.

В случайном эксперименте монету подбрасывают 2 раз. Этот эксперимент может окончиться одним из 4 элементарных событий: оба раза выпадет орёл, первый раз выпадет орёл, а второй раз – решка, первый раз выпадет решка, а второй раз – орёл, оба раза выпадет решка. Эти события равновозможны из-за симметричности монеты, и вероятность каждого из них равна .

Если же вместо того чтобы бросить монету 2 раза, мы одновременно бросим две одинаковые монеты, то элементарные события «орёл-решка» и «решка-орёл» покажутся нам одним событием, так как монеты одинаковы. Значит, в этом опыте только три элементарных события: «два орла», «две решки» и «орёл и решка».

Можно подумать, что вероятность каждого из этих событий равна  (так и посчитал Д'Аламбер). Но на самом деле эти элементарные события не являются равновозможными. Так, вероятность события «два орла» равна , вероятность события «две решки» тоже равна , а вероятность события «орёл и решка» равна .

Выполним несколько заданий.

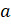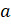Задание первое. Случайный эксперимент может окончиться одним из трёх элементарных событий: ,  и . Чему равна вероятность события , если известны вероятности событий  и ?

Решение.

Задание второе. В некотором случайном эксперименте все элементарные события равновозможны. Найдите вероятность каждого элементарного события, если всего в этом эксперименте количество элементарных событий равно: а) 15; б) 50; в) 100.

Решение.

Задание третье. Все элементарные события случайного опыта равновозможны. Сколько элементарных событий в этом опыте, если вероятность каждого равна: а) ; б) ; в) ?

Решение.

До встречи на следующих занятиях!