Решение систем неравенств с одной переменной

Давайте решим задачу: нужно заполнить водой пустой бассейн вместимостью 3000 л. Сколько литров воды в час нужно наливать в бассейн, чтобы через 2 часа он был наполнен более половины и чтобы через 3 часа бассейн не переполнился?

Решение:

Когда необходимо найти такие значения х, при которых одновременно верны два неравенства с одной переменной, их записывают совместно и говорят, что они образуют систему неравенств.

Фигурная скобка показывает, что нужно найти такие значения х, при которых оба неравенства системы обращаются в верные числовые неравенства.

Система, которую мы записали для решения задачи – это пример системы линейных неравенств с одной переменной.

Определение:

Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.

В виде системы может быть записано и любое двойное неравенство.

Например

Решить систему неравенств – значит найти все её решения или доказать, что решений нет.

Рассмотрим несколько примеров решения систем линейных неравенств с одной переменной.

Пример 1: решим систему неравенств.

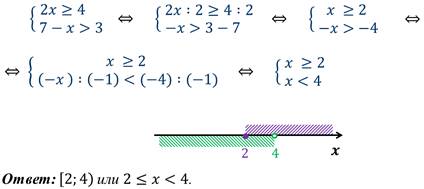
Пример 2: решим систему неравенств.

Решение:

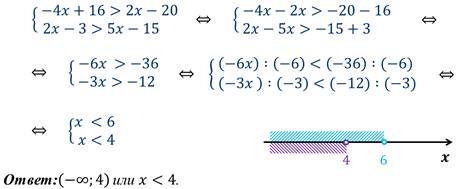
Пример 3: решим систему неравенств.

Решение:

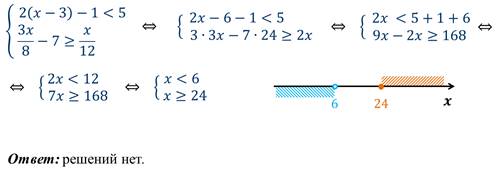
Пример 4: решим двойное неравенство.

Решение:

Запишем алгоритм решения систем линейных неравенств с одной переменной.

Для того чтобы решить систему неравенств, надо:

1. Решить каждое из неравенств системы.

2. Изобразить множество решений каждого неравенства на координатной прямой.

3. Найти пересечение промежутков (если оно есть) и записать в виде обозначения промежутка или в виде неравенства, задающего этот промежуток, или сделать вывод об отсутствии решения системы.

Итоги: