Решение неравенств с одной переменной

Ранее мы с вами изучили свойства числовых неравенств. На этом уроке нам понадобятся следующие теоремы:

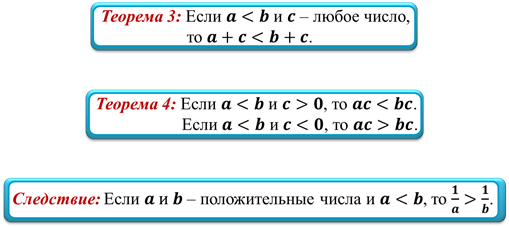
Зная основные свойства числовых неравенств, и умея их правильно применять, можно научиться решать неравенства. Чем мы и будем заниматься на этом уроке.

Итак, рассмотрим неравенство:

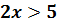
Такие неравенства называют неравенством с одной переменной или неравенством с одним неизвестным.

Но это не все решения данного неравенства. Чтобы найти все его решения, нужно рассмотреть следующие равносильные переходы.

Определение:

Решением неравенства с одной неизвестной называется значение переменной, которое обращает его в верное числовое неравенство.

Решить неравенство – это значит найти все его решения или доказать, что их нет.

Два неравенства называются равносильными, если каждое решение одного неравенства является решением другого, и наоборот, т.е. они имеют одни и те же решения. Равносильными называются и неравенства, которые не имеют решений.

Например:

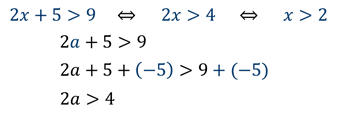
При решении неравенств используют следующие свойства:

Задание: решить неравенство:

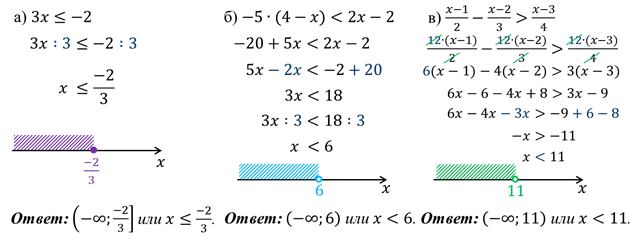
В каждом из рассмотренных примеров мы заменяли заданное неравенство равносильным ему неравенством вида 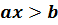 или 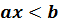, где а и b – некоторые числа.

Неравенства такого вида называют линейными неравенствами с одной переменной.

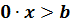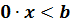Обратите внимание, в примерах мы получали линейные неравенства, в которых коэффициент при переменной не равен нулю. Но может случиться так, что при решении неравенства мы придём к линейному неравенству вида  или . Неравенство такого вида, а значит, и соответствующее исходное неравенство либо не имеют решений, либо их решением является любое число.

Например, решим неравенства:

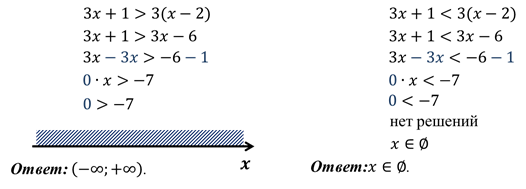
Итоги:

Неравенства вида 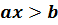, , 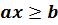,  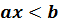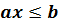называются линейными неравенствами с одной переменной.

Решением неравенства с одной неизвестной называется значение переменной, которое обращает его в верное числовое неравенство.

Решить неравенство – это значит найти все его решения или доказать, что их нет.

Два неравенства называются равносильными, если каждое решение одного неравенства является решением другого.

Равносильными называются и неравенства, которые не имеют решений.