Получите свидетельство
Вход
Как вы уже знаете, любое число можно отметить точкой на координатной прямой. Верно и обратное утверждение: каждой точке на координатной прямой соответствует какое-то число.
Также на координатной прямой можно отметить и множество чисел х, удовлетворяющих любому неравенству. Такое множество называют числовым промежутком. И в зависимости от типа неравенства выделяют виды числовых промежутков, которые имеют свои названия, обозначения и изображения на координатной прямой.
Вспомним типы неравенств.
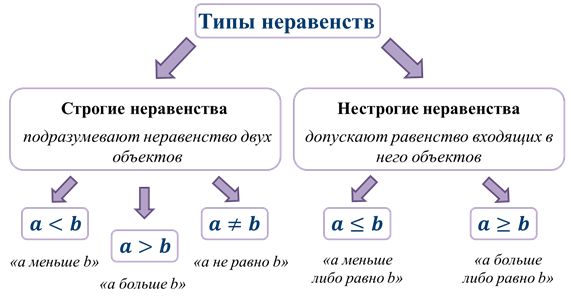
Рассмотрим виды числовых промежутков на конкретных примерах.
Пусть есть два числа: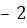 
и 
.
Множество всех чисел,
удовлетворяющих условию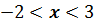 
называют интервалом.
Множество всех чисел,
удовлетворяющих условию 
называют числовым
отрезком.
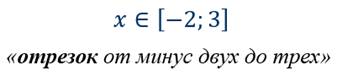
Множества чисел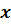 
, для которых
выполняются двойные неравенства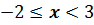 
или 
, называют полуинтервалами.
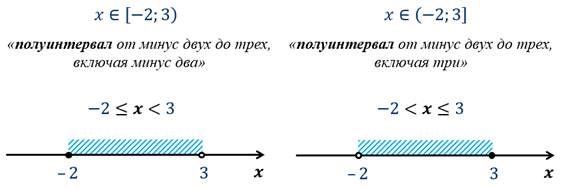
На экране вы видите, как изображают такие полуинтервалы на координатной прямой.
Как вы уже знаете, множество действительных чисел изображается всей координатной прямой. Его называют числовой прямой и обозначают так:
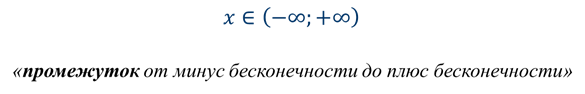
Рассмотрим другие виды числовых промежутков.
Множество чисел, удовлетворяющих
условию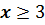 
называют числовым
лучом.
Множество чисел, удовлетворяющих
условию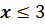 
называют числовым
лучом.
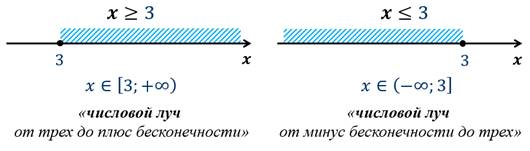
Множества чисел, удовлетворяющих
условиям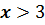 
или 
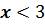называют открытым
числовым лучом.
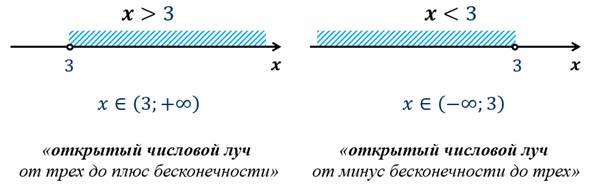
Заметим, что в обоих случаях число 3 не входит в множества.
Числовые отрезки, интервалы, полуинтервалы, числовые лучи и открытые числовые лучи называют числовыми промежутками.
Замечание: Если граничная точка в промежуток не входит, то на координатной прямой её изображают пустой точкой и в обозначении промежутка её выделяют круглой скобкой. Если же граничная точка входит в промежуток, то на координатной прямой её изображают закрашенной точкой и в обозначении промежутка выделяют квадратной скобкой.
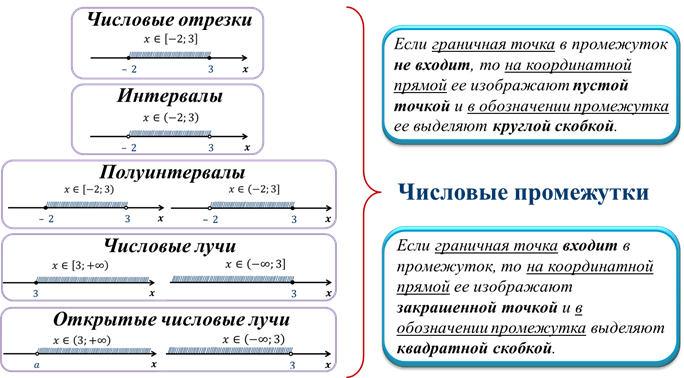
Запишем обозначения числовых
промежутков, их названия и изображение на координатной прямой для произвольных
чисел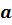 
и 
.
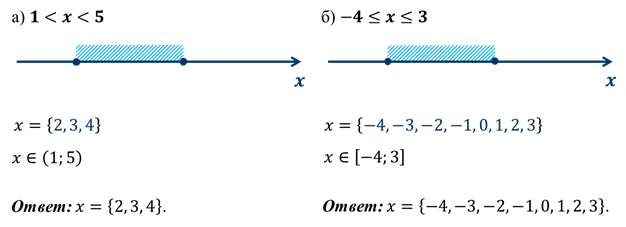
Задание: изобразить на координатной прямой множество чисел, удовлетворяющих неравенствам, и записать решение числовым промежутком.
Решение:
Задание: найдём все целые числа, удовлетворяющие неравенствам.
Решение:
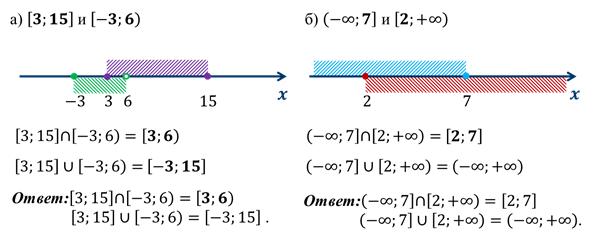
Имея представления о числовых промежутках можно находить их пересечение и объединение.
Например: найдём пересечение и объединение числовых промежутков:
Решение:
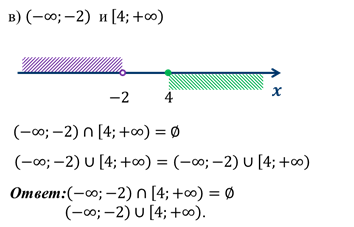
Итоги:
Интервал – это множество чисел, удовлетворяющих условию 𝑎<𝒙<𝑏.
Отрезок – это множество чисел, удовлетворяющих условию 𝑎≤𝒙≤𝑏.
Полуинтервал – это множество чисел, удовлетворяющих условиям 𝑎≤𝒙<𝑏 или 𝑎<𝒙≤𝑏.
Числовой луч – это множество чисел, удовлетворяющих условиям 𝒙≥𝑎 или 𝒙≤𝑎.
Открытый луч – это множество чисел, удовлетворяющих условиям 𝒙>𝑎 или 𝒙<𝑎.
0
17265
