Пересечение и объединение множеств

Понятие множества является одним из основных понятий математики. Оно не определяется через другие, уже известные понятия. Его смысл раскрывается лишь путём описания.

Например, множество знаков зодиака, множество животных, множество деревьев, множество точек на прямой, множество треугольников на плоскости и т.д. .

Т.е. под понятием «множества» мы понимаем совокупность некоторых объектов, объединённых по какому-нибудь общему признаку, свойству.

Определение:

Предметы, которые составляют определённое множество, называют его элементами.

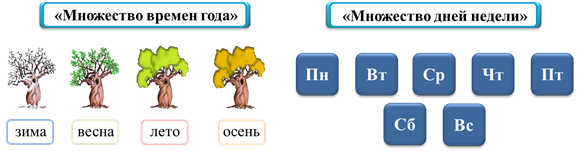
Например, множество времён года состоит из элементов: зима, весна, лето и осень. А множество дней недели из элементов: понедельник, вторник, среда, четверг, пятница, суббота и воскресенье.

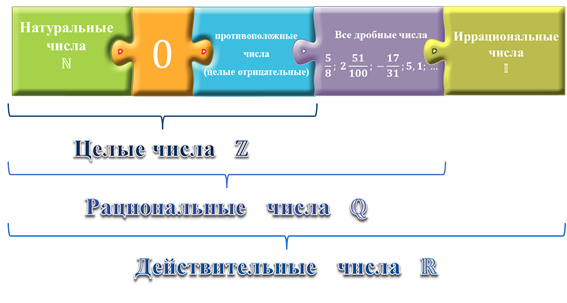
Так, в алгебре выделяют следующие множества, которые вам уже знакомы: это множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество действительных чисел.

Множества обозначают заглавными буквами латинского алфавита:

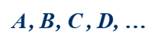
А его элементы – строчными:

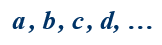
Если 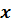 – элемент множества А, то записывают так: .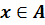

Если 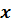 не является элементом множества А, то записывают так: .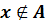

Множество, не имеющее ни одного элемента, называют пустым множеством.

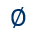
Примером, пустого множества может служить множество всех точек пересечения двух параллельных прямых. Понятно, что две параллельные прямые никогда не пересекутся и, следовательно, точек пересечения они не имеют вовсе.

Существует два типа множеств – конечные и бесконечные.

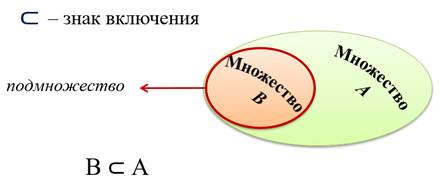
Пусть есть некоторые два множества А и В.

Пусть два множества А и В.

И пусть каждый элемент множества В является элементом множества А.

Тогда множество В является подмножеством множества А.

Пример:

Пусть А – множество натуральных делителей числа 24.

В – множество натуральных делителей числа 36.

Говорят, что множество С является пересечением множеств А и В.

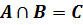
Сделаем вывод: пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.

Соотношение между множествами А, В и С можно изобразить с помощью специальных схем, которые называются кругами Эйлера. Смотрите, фигура, получившаяся при пересечении кругов (множества А и множества В), изображает множество С.

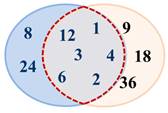
Пересечение множеств можно использовать тогда, когда надо найти элементы, которые удовлетворяют нескольким условиям.

Замечание: если два множества не имеют общих элементов, то пересечением этих множеств является пустое множество.

Напомним, что пустое множество принято обозначать таким знаком

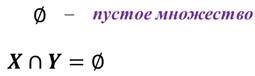
Например:

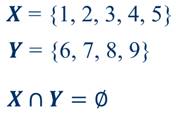
Теперь рассмотрим объединение множеств.

Пример:

Пусть А – множество натуральных делителей числа 24.

В – множество натуральных делителей числа 36.

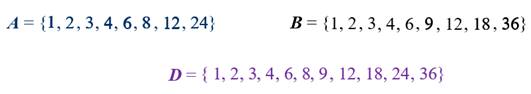
Говорят, что множество D является объединением множеств А и В.

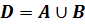
Сделаем вывод: объединением двух множеств называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.

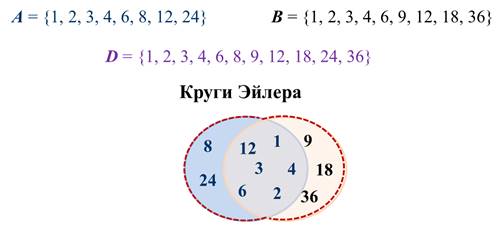
Замечание: если элемент входит в оба множества, то в объединённое он входит один раз.

Задание: даны множества А и В, причём А – множество чётных чисел не превосходящих 15, а В – множество двузначных чисел не превосходящих 20. Задайте множества А и В перечислением элементов и найдите их пересечение и объединение.

Решение:

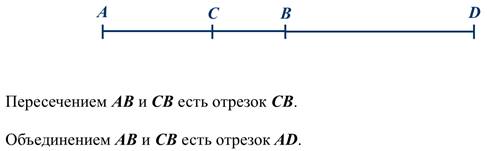
Задание: на экране изображены два отрезка АВ и CD. Какая фигура является: пересечением этих отрезков, объединением этих отрезков?

Решение:

Итоги:

Множество это совокупность некоторых объектов, объединённых по какому-нибудь общему признаку, свойству.

Предметы, которые составляют определённое множество, называют его элементами.

Пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.

Объединением двух множеств называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.