При измерении длин отрезков и площадей фигур, при взвешивании тел и других измерениях получаются числа, выражающие эти величины.

Ввиду погрешностей измерения полученные числа являются приближёнными значениями измеряемой величины.
У каждого из вас есть линейка и карандаш. Давайте попытаемся измерить длину карандаша.

Из рисунка видно, что длина карандаша чуть меньше 10 см. Если бы на этой линейке не было миллиметровых делений, то мы бы сказали, что длина карандаша равна 10 см. Но это было бы не совсем точное измерение.
Такую неточность называют погрешностью измерения.
В нашем случае, на линейке есть миллиметровые деления, поэтому мы можем измерить длину карандаша с более высокой точностью – 9,8 см.
Приближённое значение отличается от точного значения в этом случае на 0,2 см. Чтобы узнать, на сколько приближённое значение отличается от точного, надо из большего числа вычесть меньшее, т.е. найти модуль разности точного и приближённого значений. Этот модуль разности называют абсолютной погрешностью.

Определение:
Абсолютной погрешностью приближённого значения называют модуль разности точного и приближённого значений.
Значение абсолютной погрешности не всегда можно найти. Но обычно известна её оценка сверху – например, при измерении длины отрезка линейкой с сантиметровыми делениями абсолютная погрешность измерения не превышает 1 сантиметра, а при взвешивании на весах с гирями 100 грамм, 200 грамм, 500 грамм и 1 килограмм абсолютная погрешность взвешивания не превышает ста грамм.
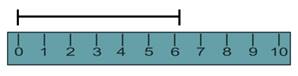

Посмотрите, на слайде изображён отрезок CD.
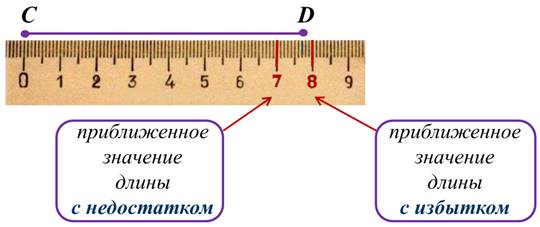
Его длина расположена между цифрами 7 см и 8 см. Понятно, что 7 см – это приближённое значение длины отрезка CD с недостатком, а 8 см – это приближённое значение длины отрезка CD с избытком.
Если истинную длину отрезка обозначить за х, то получим, что длина отрезка CD удовлетворяет неравенству:
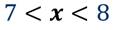
Пусть истинное
значение измеряемой величины равно 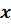 .
.
Измерение дало
результат 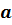 .
.
Тогда разность 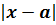 – это абсолютная погрешность измерения.
– это абсолютная погрешность измерения.
Число 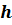 называют границей абсолютной погрешности
измерения, если выполняется неравенство:
называют границей абсолютной погрешности
измерения, если выполняется неравенство:
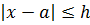
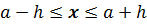
Принято писать 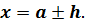
Точность приближённого значения зависит от многих причин. Если приближённое значение получено в процессе измерения, то, конечно же, его точность будет зависеть от прибора, с помощью которого выполнялось это измерение.
Вот, например, комнатный термометр. На нём деления нанесены через один градус. Это даёт возможность измерять температуру воздуха с точностью до 1 градуса. А на весах, у которых цена деления шкалы 20 г, можно взвешивать с точностью до 20 г. Или, к примеру, ещё, механические часы. Цена одного деления, которых 1 мин. По ним можно сказать время с точностью до 1 минуты.
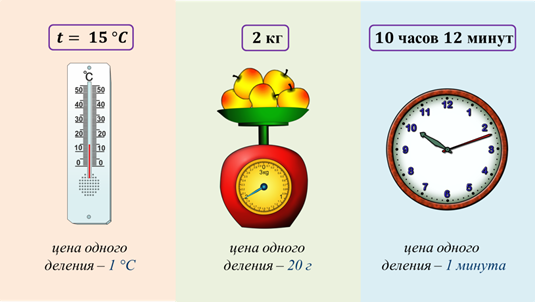
Для оценки качества измерения можно использовать относительную погрешность приближённого значения.
Определение:
Относительной погрешностью приближённого значения называется отношение абсолютной погрешности к модулю приближённого значения.
Относительную погрешность принято выражать в процентах. В тех случаях, когда абсолютная погрешность приближенного значения неизвестна, а известна лишь его точность, ограничиваются оценкой относительной погрешности.
Например: при измерении (в сантиметрах) длины книжной полки и толщины компакт-диска получили следующие результаты:
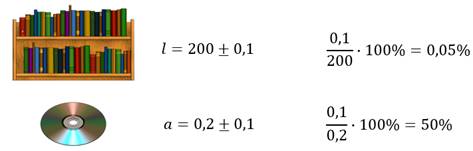
Чем меньше относительная погрешность измерения, тем оно точнее.
Итоги:
Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
Число 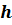 называют границей абсолютной погрешности измерения,
если выполняется неравенство:
называют границей абсолютной погрешности измерения,
если выполняется неравенство:
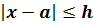
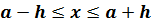
Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения.
Чем меньше относительная погрешность измерения, тем оно
точнее.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 15415
15415



