Сложение и умножение числовых неравенств

Вспомним основные свойства числовых неравенств, которые мы уже знаем.  

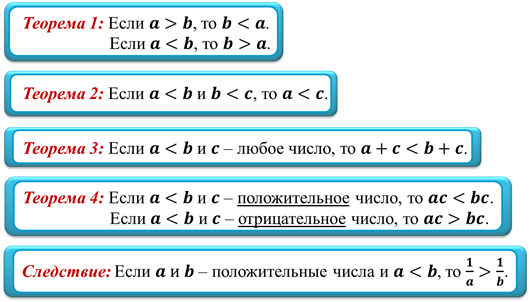
При решении различных задач часто приходится складывать или умножать почленно левые и правые части неравенств.

Рассмотрим, как выполняется сложение и умножение числовых неравенств.

Теорема 5: Если  и , то .

Доказательство:

Прибавим к  число .

Получим .

Прибавим к  число .

Следовательно, .

Если почленно сложить верные неравенства одного знака, то получится верное неравенство.

Теорема 6: Если  и , где , ,  и  – положительные числа, то .

Доказательство:

Умножим  на число .

Получим .

Умножим  на число .

Получим .

Если почленно перемножить верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство.

Если среди чисел , ,  и  имеются отрицательные, то неравенство  может оказаться неверным!

Следствие: Если числа  – положительные и , то , где  – натуральное число.

Доказательство:

Доказанные свойства неравенств часто используют при оценке суммы, разности, произведения и частного.

Задание: Пусть есть неравенства  и . Оцените значения выражений: а)    и    б) .

Решение:

Задание 2: пусть есть неравенства  и . Оцените значения выражений: а)    и    б) .

Решение:

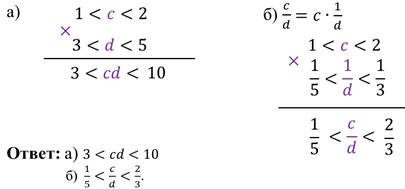
Итоги:

Теорема 5: Если 𝒂<𝒃 и 𝒄<𝒅, то 𝒂+𝒄<𝒃+𝒅.

Теорема 6: Если 𝒂<𝒃 и 𝒄<𝒅, где 𝒂, 𝒃, 𝒄 и 𝒅 – положительные числа, то 𝒂𝒄<𝒃𝒅.

Следствие: Если числа 𝒂 и 𝒃 – положительные и 𝒂<𝒃, то <, где 𝒏 – натуральное число.